Równanie Taita

W mechanice płynów równanie Taita jest równaniem stanu , używanym do powiązania gęstości cieczy z ciśnieniem hydrostatycznym . Równanie zostało pierwotnie opublikowane przez Petera Guthrie Taita w 1888 roku w formie

${\ Displaystyle {\ Frac {V_ {0} -V} {PV_ {0}}} = {\ Frac {A} {\ Pi + P}}}$

gdzie $jest$$ciśnieniem$ hydrostatycznym oprócz ciśnienia atmosferycznego, $objętość$ objętość pod ciśnieniem atmosferycznym, pod $.$$}$$parametrami określonymi$ i . Bardzo szczegółowe badanie historyczne równania Taita z fizyczną interpretacją dwóch parametrów i ${\ displaystyle A}$${\ Displaystyle \ Pi}$ podano w odniesieniu.

Równanie stanu Taita-Tammanna

W 1895 roku oryginalne izotermiczne równanie Taita zostało zastąpione przez Tammanna równaniem postaci

${\ Displaystyle {K} = - {V_ {0}} \ lewo ({\ Frac {\ częściowe P} {\ częściowe V}} \right)_{T}={V_{0}}{\frac {(B+P)}{C}}}$

gdzie $jest$ mieszanym modułem objętościowym. Powyższe równanie jest powszechnie znane jako równanie Taita . Zintegrowany formularz jest powszechnie napisany

${\ Displaystyle V = V_ {0} -C \ log \ lewo ({\ Frac {B + P} {B + P_ {0}}} \ prawo )}$

Gdzie

• ${\ Displaystyle V \}$ to określona objętość substancji (w jednostkach ml / g lub m ³ / kg)
• ${\ Displaystyle V_ {0}}$ to określona objętość w ${\ Displaystyle P = P_ {0}}$
• $} (te$$\ Displaystyle B$$co$ jednostki $)$ i (te same jednostki ) są funkcjami temperatury

Formuła ciśnienia

Wyrażenie na ciśnienie wyrażone w objętości właściwej to

${\ Displaystyle P = (B + P_ {0}) \ exp \ lewo (- {\ Frac {VV_ {0}} {C}} \ prawej) -B \,.}$

$B}$ Taita-Tammanna z fizyczną interpretacją dwóch parametrów empirycznych i $displaystyle$ podano w rozdziale 3 odnośników. Wyrażenia w funkcji temperatury dla dwóch parametrów empirycznych i są podane $dla wody, wody morskiej,$${\ Displaystyle T_ {c}}$$T.$ do temperatury krytycznej . Szczególny przypadek przechłodzonej fazy wody omówiono w Dodatku D odnośnika.

Równanie stanu Taita-Murnaghana

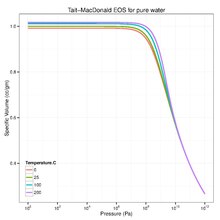
Objętość właściwa jako funkcja ciśnienia przewidywanego przez równanie stanu Taita-Murnaghana.

Innym popularnym izotermicznym równaniem stanu, które nosi nazwę „równanie Taita”, jest model Murnaghana , który czasami wyraża się jako

${\ Displaystyle {\ Frac {V} {V_ {0}}} = \ lewo [1 + {\ Frac {n} {K_ {0} }}}\,(P-P_{0})\right]^{-1/n}}$

gdzie ${\ displaystyle V}$ to objętość właściwa pod ciśnieniem , ${\ displaystyle V_ {0}}$$to$ objętość właściwa pod ciśnieniem ${0}}$ , ${\ displaystyle K_ {0}}$$to$ moduł objętościowy w $,$ jest materiałowym.

Formuła ciśnienia

To równanie w postaci ciśnienia można zapisać jako

${\ Displaystyle P = {\ Frac {K_ {0}}{n}} \ lewo [\ lewo ({\ Frac {V_ {0}} {V}} \ prawo) ^ {n} -1 \ prawo] + P_{0}={\frac {K_{0}}{n}}\left[\left({\frac {\rho }{\rho _{0}}}\right)^{n}-1\ prawo]+P_{0}.}$

gdzie $rho, \ rho _ {0}}$ \ $są$ masowymi Dla czystej wody typowe parametry to = 101325 Pa, ${\ Displaystyle \ rho _ {0}}$$=$ kg/m3, ${\ Displaystyle K_ {0}}$ = 2,15 GPa i ${\ displaystyle n}$ = 7,15.

Zauważ, że ta postać równania stanu Tate'a jest identyczna z równaniem stanu Murnaghana .

Formuła modułu objętościowego

Styczny moduł objętościowy przewidywany przez model MacDonalda – Taita wynosi

${\ Displaystyle K = K_ {0} \ lewo ({\ Frac {V_ {0}} {V}} \ prawej) ^ {n} \,.}$

Równanie stanu Tumlirza – Tammanna – Taita

Równanie stanu Tumlirza-Tammanna-Taita oparte na dopasowaniach do danych doświadczalnych dla czystej wody.

Powiązanym równaniem stanu, które można wykorzystać do modelowania cieczy, jest równanie Tumlirza (czasami nazywane równaniem Tammanna i pierwotnie zaproponowane przez Tumlirza w 1909 r. I Tammanna w 1911 r. Dla czystej wody). Ta relacja ma postać

${\ Displaystyle V (P, S, T) = V _ {\ infty} -K_ {1} S + {\ Frac {\lambda} {P_{0}+K_{2}S+P}}}$

gdzie ${\ Displaystyle V (P, S, T)}$$określona$ objętość, to ciśnienie, to zasolenie, $}$${\ Displaystyle$${\ Displaystyle V _ {\ infty$ temperatura, a objętość właściwa, gdy , $}$${\ displaystyle K_ {1}, K_ {2}, P_ {0}}$ to parametry, które można dopasować do danych eksperymentalnych.

Wersja Tumlirza-Tammanna równania Taita dla słodkiej wody, tj. gdy ${\ displaystyle S = 0} to S = {\ displaystyle S = 0$ }

${\ Displaystyle V = V _ {\ infty} + {\ Frac {\ lambda} {P_ {0} + P}} \,.}$

W przypadku czystej wody zależność od temperatury wynosi: ${\ Displaystyle V_ {\ infty}, \ lambda, P_ {0}}$

${\ Displaystyle {\ rozpocząć {wyrównane} \ lambda & = 1788,316 + 21,55053 \, T-0,4695911 \, T ^ {2} + 3,096363 \ razy 10 ^ {-3} \, T ^ {3} -0,7341182 \ razy 10 ^{-5}\,T^{4}\\P_{0}&=5918,499+58,05267\,T-1,1253317\,T^{2}+6,6123869\razy 10^{-3}\,T^{ 3}-1,4661625\times 10^{-5}\,T^{4}\\V_{\infty }&=0,6980547-0,7435626\times 10^{-3}\,T+0,3704258\times 10^{- 4}\,T^{2}-0,6315724\razy 10^{-6}\,T^{3}\\&+0,9829576\razy 10^{-8}\,T^{4}-0,1197269\razy 10^{-9}\,T^{5}+0,1005461\razy 10^{-11}\,T^{6}\\&-0,5437898\razy 10^{-14}\,T^{7} +0,169946\razy 10^{-16}\,T^{8}-0,2295063\razy 10^{-19}\,T^{9}\end{wyrównane}}}$

W powyższych dopasowaniach temperatura $}$ w stopniach Celsjusza, w barach, $displaystyle$ cm3 / gm, a ${\ displaystyle \ lambda}$$T$ jest w barach-cc/gm.

Formuła ciśnienia

Odwrotna zależność Tumlirza – Tammanna – Taita dla ciśnienia w funkcji objętości właściwej to

${\ Displaystyle P = {\ Frac {\ lambda} {V-V_ {\ infty}}} -P_ {0} \,.}$

Formuła modułu objętościowego

Wzór Tumlirza-Tammanna-Taita na chwilowy styczny moduł objętościowy czystej wody jest funkcją kwadratową (alternatywnie patrz ) ${\ displaystyle P}$

${\ Displaystyle K = - V \, {\ Frac {\ częściowe P} {\ częściowe V}} = {\ Frac {V \, \ lambda} {(VV_ {\ infty}) ^ {2}}} =(P_{0}+P)+{\frac {V_{\infty}}{\lambda }}(P_{0}+P)^{2}\,.}$

Zmodyfikowane równanie stanu Taita

W szczególności po badaniu eksplozji podwodnych, a dokładniej emitowanych fal uderzeniowych, JG Kirkwood zaproponował w 1965 r. Bardziej odpowiednią postać równania stanu do opisu wysokich ciśnień (> 1 kbar) poprzez wyrażenie izentropowego współczynnika ściśliwości jako

${\ Displaystyle - {\ Frac {1} {V}} \ lewo ({\ Frac {\ częściowe V} {\ częściowe P}} \ prawo)_{S}={\frac {1}{n(B+P)}}}$

gdzie $reprezentuje tutaj$ . Dwa parametry empiryczne i są teraz funkcją entropii taką, że $displaystyle$$n}$

• ${\ displaystyle n \}$ jest bezwymiarowy
• ${\ displaystyle B \}$ ma te same jednostki co ${\ displaystyle P}$

Całkowanie prowadzi do następującego wyrażenia dla objętości wzdłuż izentropii $(P,$$S)}$

${\ Displaystyle {\ Frac {V} {V_ {0}}} = \ lewo (1 + {\ Frac {P_ { 0}}{B}}\right)^{1/n}\left(1+{\frac {P}{B}}\right)^{-1/n}}$

gdzie ${\ Displaystyle V_ {0} = V (P_ {0}, S)}$ .

Formuła ciśnienia

Wyrażenie na ciśnienie w odniesieniu do objętości właściwej wzdłuż izentropii $\ Displaystyle P ($ P. $V, S)}$

${\ Displaystyle P = (B + P_ {0}) \, \ lewo ({\ cfrac {V_ {0}} {V}} \ prawej) ^ {n} -B \,.}$

$.$ badanie zmodyfikowanego równania stanu Taita z fizyczną interpretacją dwóch parametrów empirycznych $i$ podano w rozdziale 4 odnośników Wyrażenia jako funkcja entropii dla dwóch parametrów empirycznych $są$ podane $dla$ wody, helu-3 i helu-4

Zobacz też

• Równanie stanu