Rezonans magnetyczny (mechanika kwantowa)

Rezonans magnetyczny to kwantowo-mechaniczny efekt rezonansowy , który może pojawić się, gdy dipol magnetyczny zostanie wystawiony na działanie statycznego pola magnetycznego i zaburzony innym, oscylującym polem elektromagnetycznym . Ze względu na pole statyczne dipol może przyjąć szereg dyskretnych stanów własnych energii , w zależności od wartości jego momentu pędu, liczby kwantowej . Oscylujące pole może wówczas z pewnym prawdopodobieństwem iz określoną szybkością przejść dipol między swoimi stanami energetycznymi. częstotliwości pola, a szybkość będzie zależała od jego amplitudy . Kiedy częstotliwość tego pola prowadzi do maksymalnego możliwego prawdopodobieństwa przejścia między dwoma stanami, uzyskano rezonans magnetyczny. W takim razie energia fotonów tworzących oscylujące pole odpowiada różnicy energii między tymi stanami. Jeśli dipol jest łaskotany polem oscylującym daleko od rezonansu, jest mało prawdopodobne, aby przeszedł. Jest to analogiczne do innych efektów rezonansowych, takich jak wymuszony oscylator harmoniczny . Okresowe przejście między różnymi stanami nazywa się cyklem Rabi , a tempo, w jakim to się dzieje, nazywa się częstotliwością Rabi . Częstotliwości Rabi nie należy mylić z własną częstotliwością pola. Od wielu jąder atomowych gatunek może zachowywać się jak dipol magnetyczny, ta technika rezonansu jest podstawą magnetycznego rezonansu jądrowego , w tym obrazowania magnetycznego rezonansu jądrowego i spektroskopii magnetycznego rezonansu jądrowego .

Wyjaśnienie mechaniki kwantowej

Jako dipol magnetyczny, używając układu spinowego $, takiego$ proton zgodnie z kwantowo-mechanicznym stanem układu, oznaczonym przez : $t$ ja $t}/\hbar }}$$^ {-i {{$ \ ; wynik jest zgodny z równaniem Schrödingera :

                        ${\ Displaystyle i \ hbar {\ Frac {\ częściowy} {\ częściowy t}} \ psi = {\ kapelusz {H}} \ psi}$

Stany o określonej energii ewoluują w czasie z fazą ${\ Displaystyle |\ Psi (t) \ rangle =|\ Psi (0) \ rangle e ^ {-iEt / \ hbar}} )$${\ Displaystyle e ^ {-iEt / \ hbar}}$ ( gdzie E jest energią stanu, ponieważ prawdopodobieństwo znalezienia systemu w stanie ${\ Displaystyle |\ langle x | \ Psi (t) \ rangle | ^ {2}}$ = ${\ Displaystyle |\ langle x | \ Psi (0) \ rangle | ^ {2}}$ jest niezależny od czasu. Takie stany nazywane są stanami stacjonarnymi , więc jeśli układ jest przygotowany w stanie stacjonarnym (tj. jednym ze stanów własnych operatora hamiltonowskiego ), to P(t)=1, czyli pozostaje w tym stanie w nieskończoność. Dotyczy to tylko systemów izolowanych. Kiedy system w stanie stacjonarnym jest zaburzony, jego stan się zmienia, więc nie jest już stanem własnym kompletnego hamiltonianu systemu. To $samo$ zachodzi w rezonansie magnetycznym dla układu spinowego polu magnetycznym.

Hamiltonian dipola magnetycznego $($ z cząstką spinową $)$ w polu $styl wyświetlania \mathbf {B_{0}} =B_{0}{\kapelusz {z}}}$${$ to:

                        ${\ Displaystyle {\ kapelusz {H}} = - \ mathbf {m} \ cdot \ mathbf {B_ {0 }} =-{\tfrac {\hbar }{2}}\gamma \sigma _{z}B_{0}=-{\tfrac {\hbar }{2}}\omega _{0}{\begin{ bmacierz}1&0\\0&-1\end{bmacierz}}}$

Tutaj $\ omega _ {0}: = \ gamma B_ {0}}$$Displaystyle$ jest częstotliwością precesji Larmora dla pola magnetycznego i ${\ Displaystyle \ sigma _ {z}}$ jest z matrycą Pauliego . Tak więc wartości własne ${\ Displaystyle {\ hat {H}}}$ to ${\ Displaystyle - {\ tfrac {\ hbar} {2}} \ omega _ {0}}$ i ${\ Displaystyle {\ tfrac {\ hbar} {2}} \ omega _ {0}}$ . Jeśli system jest zaburzony przez słabe pole magnetyczne , obracające się w kierunku przeciwnym do ruchu wskazówek zegara w płaszczyźnie xy (normalnej do ) z częstotliwością kątową ${\ Displaystyle \ mathbf {B_ {1}}$$}$${\ Displaystyle \ omega}$ , tak że ${\ Displaystyle \ mathbf {B_ {1}} = {\ kapelusz {i}} B_ {1} \ cos {\ omega t} - {\ kapelusz {j}} B_ {1} \ sin {\ omega t}}$ , to ${\ Displaystyle {\ rozpocząć {bmatrix} 1 \\ 0 \ koniec {bmatrix}}}$ i ${\ Displaystyle {\ rozpocząć {bmatrix} 0 \\ 1 \ koniec {bmatrix}}$ } nie stany własne hamiltonianu, który jest modyfikowany

      ${\ Displaystyle {\ kapelusz {H}} = \ gamma {\ rozpocząć {pmatrix} \ mathbf {B_ {0}} & \ mathbf {B_ {1}} \ e ^ {\ omega to} \\\ mathbf {B_ {1}} e^{-\omega to}&\mathbf {-B_{0}} \end{pmatrix}}.}$

Niewygodne jest radzenie sobie z zależnym od czasu hamiltonistą. Aby uczynić $,$ wymagany jest nowy układ odniesienia obracający się z $styl wyświetlania {\ kapelusz {R}} (t)}$$tj$ . operatorem ${$ na ${\ Displaystyle | \ Psi (t) \ rangle}$ , co jest równoznaczne ze zmianą podstawy w przestrzeni Hilberta . Wykorzystując to w równaniu Schrödingera, hamiltonian staje się:

               ${\ Displaystyle {\ kapelusz {H ^ {\ pierwsza}}} = R (t) {\ kapelusz {H}} R ( t)^{\sztylet}+{\tfrac {\hbar }{2}}\omega \sigma _{z}}$

R $)}$ na podstawie as- σ $\ Displaystyle \ sigma _ {z}}$

               ${\ Displaystyle {\ kapelusz {R}} (t) = {\ rozpocząć {pmatrix} e ^ {-i {\ omega} t/2}&0\\0&e^{i{\omega}t/2}\end{pmatrix}}}$

Używając tej formy Hamiltonianu, znaleziono nową podstawę :

Wykres amplitudy prawdopodobieństwa odwrócenia spinu w rezonansie

Wykres amplitudy prawdopodobieństwa odwrócenia spinu przy braku rezonansu

           ${\ Displaystyle {\ kapelusz {H ^ {\ pierwsza}}} = {\ tfrac {\ hbar}} {2}} {\ rozpocząć { pmatrix} \ Delta \ omega &- \ omega _ {1} \\ - \ omega _ {1} & - \ Delta \ koniec {pmatrix}}} gdzie Δ ω = ω -$ ω $omega =\omega -\omega _{0}}$ i ${\ Displaystyle \ omega _ {1} = \ gamma B_ {1}}$                    

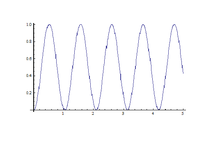
Ten hamiltonian jest dokładnie podobny do układu dwustanowego z niezakłóconymi energiami ${\ Displaystyle {\ tfrac {\ hbar}} {2}} \ Delta \ omega}$ & ${\ Displaystyle - {\ tfrac {\ hbar {2}} \ Delta \ omega}$ z zaburzeniem wyrażonym przez ${\ Displaystyle {\ tfrac {\ hbar}} {2}} {\ rozpocząć {pmatrix} 0& -\omega _{1}\\-\omega _{1}&0\end{pmatrix}}}$ ; Według oscylacji Rabiego , zaczynając od stanu, dipol równolegle do stanu ${\ Displaystyle {\ rozpocząć {bmatrix} 1 \\ 0 \ koniec {bmatrix}$$}$ z energią ${\ Displaystyle - {\ tfrac {\ hbar} {2}} \ omega _ {0}}$ , prawdopodobieństwo, że przejdzie do ${\ Displaystyle {\ rozpocząć {bmatrix} 0 \ \1\end{bmatrix}}}$ stan (tj. nastąpi odwrócenie) jest

${\ Displaystyle P_ {12} = {\ Frac {|\ omega _ {1} ^ {2} |} {| \ Delta \ omega ^ {2} + \omega _{1}^{2}|}}\sin ^{2}[{\sqrt {\omega ^{2}+\Delta \omega ^{2}}}t/2]}$

Rozważmy teraz $= ω {\ Displaystyle \ omega = \$ pole oscyluje z taką samą szybkością, jak $}$$_$ tak. To jest przypadek rezonansu . Wtedy w określonych punktach w czasie, mianowicie ${\ Displaystyle t = {\ Frac {(2n + 1) \ pi} {\ sqrt {\ omega ^ {2} + \ Delta \ omega ^ {2}}}}}, dipol obróci się, przechodząc do$ drugiego stan własny energii ${\ Displaystyle {\ rozpocząć {bmatrix} 0 \\ 1 \ koniec {bmatrix}}}$ ze 100% prawdopodobieństwem. Kiedy $jest$ zmiany stanu energetycznego Dlatego warunek rezonansu można wykorzystać na przykład do pomiaru momentu magnetycznego dipola lub pola magnetycznego w punkcie w przestrzeni.

Specjalny przypadek do pokazania aplikacji

$,$ gdy system oscyluje między dwoma niestabilnymi poziomami, które mają ten sam czas . Jeśli atomy są wzbudzane $,$ do pierwszego stanu, część rozpada się, a reszta ma prawdopodobieństwo przejścia do drugiego stanu, więc w przedziale czasu między t oraz (t+dt) liczba atomów, które przeskakują do drugiego stanu z pierwszego wynosi ${\ Displaystyle n (1-e ^ {- t / \ tau}) P_ {12} dt}$ , więc w czasie t liczba atomów w drugim stanie wynosi

Wykres szybkości rozpadu ze zmiennością jednolitego pola magnetycznego ${\ displaystyle B_ {0}}$

Wykres połowy szerokości krzywej Lorentza ze zmianą ${\ Displaystyle B_ {1}}$

                        ${\ Displaystyle dN = ne ^ {- t / \ tau}. (1-e ^ {- t / \ tau}) P_ {12} dt}$ = ${\ Displaystyle ne ^ {- t / \ tau}. P_ {12} dt}$ 

Szybkość rozpadu ze stanu drugiego zależy od liczby atomów, które zostały zebrane w tym stanie ze wszystkich poprzednich przedziałów, więc liczba atomów w stanie 2 wynosi ${\ Displaystyle \ int _{-\infty}^{0}ne^{-t/\tau}P_{12}\ dt}$ ; Szybkość rozpadu atomów ze stanu drugiego jest proporcjonalna do liczby atomów obecnych w tym stanie, podczas gdy stała proporcjonalności to stała rozpadu ${\ displaystyle \ lambda}$ . Wykonanie całkowania szybkości rozpadu atomów ze stanu drugiego uzyskuje się jako:

                                 ${\ Displaystyle (n/2) \ omega ^ {2} / (\ delta \ omega ^ {2} + \ omega _ {1}^{2}+1/\tau ^{2})}$

Z tego wyrażenia można wyciągnąć wiele interesujących punktów, np

• $delta$ pole magnetyczne tak, że w $\ omega}$${\ Displaystyle \$ tworzy krzywą Lorentza (patrz rozkład Cauchy'ego – Lorentza ), wykrywanie b { szczyt tej krzywej, jej odcięta daje , więc teraz $Displaystyle \ mathbf$ częstotliwość kątowa obrotu $B} _ { 1}}$${$ = ${\ Displaystyle \ gamma}$$}}$ { $max$ , więc ze znanej wartości ${\ Displaystyle (B_ {0}) _ {max}}$ , można zmierzyć współczynnik $;$ dipola tą metodą możemy zmierzyć spin jądrowy , w którym wszystkie spiny elektroniczne są zrównoważone. Prawidłowy pomiar jądrowego momentu magnetycznego pomaga zrozumieć charakter siły jądrowej.
• Jeśli wiadomo, zmieniając wartość ${ \$ uzyskać $displaystyle \ gamma$$}$ Ta technika pomiarowa jest wystarczająco precyzyjna, aby można ją było stosować w czułych magnetometrach. Za pomocą tej techniki można uzyskać wartość pola magnetycznego działającego w określonym miejscu sieci przez jego otoczenie wewnątrz kryształu.
• Mierząc $_$ _ kilka wartości (tj. ${\ Displaystyle B_ {1}}$$)$ , możemy wykreślić re vs ${\ Displaystyle \ omega _ {1}$ przez ekstrapolując tę ​​​​linię dla $przecięcia$ czas życia stanów niestabilnych można uzyskać z punktu

Metoda Rabiego

Zobacz także: eksperyment Sterna – Gerlacha

Aparatura sugerowana i używana przez Rabi

Istnienie spinowego momentu pędu elektronów zostało odkryte eksperymentalnie w eksperymencie Sterna – Gerlacha . W badaniu tym przez niejednorodne pole magnetyczne przepuszczano wiązkę neutralnych atomów z jednym elektronem na powłoce walencyjnej , nieposiadających pędu orbitalnego (z punktu widzenia mechaniki kwantowej). Proces ten nie był przybliżony ze względu na mały kąt odchylenia, co skutkowało znaczną niepewnością mierzonej wartości rozszczepionej belki.

Metoda Rabiego była ulepszeniem w stosunku do metody Stern-Gerlacha. Jak pokazano na rysunku, źródło emituje wiązkę neutralnych atomów, mających spinowy moment pędu ${\ displaystyle \ hbar / 2}$ . Wiązka przechodzi przez serię trzech ustawionych w jednej linii magnesów. $($ dużym gradiencie jak w Stern-Gerlach), więc atomy mające spin „w górę” gdzie ${\ Displaystyle S_ {z} = \ hbar / 2}$ ) odchyli się w dół (ścieżka 1), tj. do obszaru mniejszego pola magnetycznego B, aby zminimalizować energię. Atomy o spinie „w dół” z ${\ Displaystyle S_ {z} = - \ hbar / 2}$ ) podobnie odchyli się w górę (ścieżka 2). Wiązki przechodzą przez szczelinę 1, aby zredukować wpływ źródła poza nią. Magnes 2 wytwarza tylko jednorodne pole magnetyczne w kierunku pionowym, nie wywierając żadnej siły na wiązkę atomową, a magnes 3 jest w rzeczywistości odwróconym magnesem 1. W obszarze między biegunami magnesu 3 atomy mające spin „w górę” są wypychane w górę i atomy mając obrót „w dół”, odczuwają pchnięcie w dół, więc ich ścieżka pozostaje odpowiednio 1 i 2. Wiązki te przechodzą przez drugą szczelinę S2 i docierają do detektora i zostają wykryte.

Jeśli poziome pole wirujące , $okrągłych$$.$ obrotu jest przyłożona obszarze między biegunami magnesu 2, wytwarzanym przez oscylujący prąd w wtedy istnieje prawdopodobieństwo, że atomy przejdą przez nie z jednego stanu wirowania do drugiego ( ${\ Displaystyle S_ {z} = + \ hbar / 2-> - \ hbar / 2}$ i odwrotnie), gdy ${\ Displaystyle \ omega _ {1}}$ = ${\ Displaystyle \ omega _ {p}}$ Częstotliwość Larmora precesji momentu magnetycznego w B. Atomy, które przechodzą z „w górę” na „w dół” ' spin napotka siłę skierowaną w dół podczas przechodzenia przez magnes 3 i będzie podążał ścieżką 1'. Podobnie atomy, które zmieniają spin „w dół” na „w górę”, będą podążać ścieżką 2 ”, a atomy te nie dotrą do detektora, powodując minimalną liczbę detektorów. Jeżeli częstotliwość kątowa ${\ displaystyle \ omega _ {1}}$ z ${\ displaystyle B_ {1}}$ zmienia się w sposób ciągły, wtedy zostanie uzyskane minimum prądu detektora (kiedy = ${\ displaystyle \ omega _ {1}}$ = ${\ Displaystyle \ omega _ {p}}$ ). $_$ znanej wartości $g$ Land _ _ _ '), uzyskuje się „czynnik Landé g”, który umożliwi uzyskanie prawidłowej wartości momentu magnetycznego ${\ Displaystyle \ mu (= gq \ hbar / {4 m})}$ . Ten eksperyment, przeprowadzony przez Isidora Isaaca Rabiego, jest bardziej czuły i dokładny niż Stern-Gerlach.

Zgodność wyjaśnień klasycznych i mechaniki kwantowej

Zobacz też: Jądrowy_rezonans_magnetyczny § Teoria_jądrowego_rezonansu_magnetycznego

Zobacz też: równania Blocha

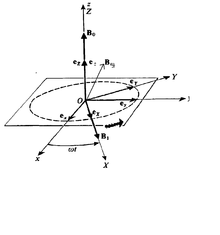
Chociaż pojęcie spinowego momentu pędu pojawia się tylko w mechanice kwantowej i nie ma klasycznego odpowiednika, zjawisko rezonansu magnetycznego można do pewnego stopnia wyjaśnić za pomocą fizyki klasycznej. Patrząc z układu odniesienia przymocowanego do wirującego pola, wydaje się, że dipol magnetyczny precesuje wokół wypadkowego pola magnetycznego ${\ Displaystyle (\ Delta \ omega {\ hat {z }}-\omega _{1}{\hat {X}})/\gamma }$ , gdzie ${\ Displaystyle {\ kapelusz {z}}}$ jest wektorem jednostkowym wzdłuż jednolitego pola magnetycznego $Displaystyle$ jest taki sam w kierunku obrotu ${\ hat {X}}}$ pole ${\ Displaystyle B_ {1}}$ i ${\ Displaystyle \ delta \ omega = \ omega - \ omega _ {0}}$ .

Dowód klasycznego wyrażenia dla precesji

Obrazkowe przedstawienie klasycznej precesji Larmora Elektrodynamika klasyczna mówi nam, że moment obrotowy na dipolu magnetycznym wynosi ${\ Displaystyle \ mathbf {m}}$ , więc jego równanie ruchu to ${\ displaystyle \ mathbf {m} \ times \ mathbf {B}}$ ${\ Displaystyle {\ Frac {d \ mathbf {L}}} {dt}} = \ mathbf {m} \ razy \ mathbf {B}} , (gdzie$ L $\ Displaystyle \ mathbf {{ L} }$ to moment pędu związany z dipolem), więc - ${\ Displaystyle {\ Frac {d \ mathbf {m}} {dt}} = \ gamma \ mathbf {m} \ razy \ mathbf {B}}$ W rozważanym przypadku dipol znajduje się pod działaniem pola magnetycznego i stąd $\ mathbf {B} _ {1}$$displaystyle$ ${\ Displaystyle {\ Frac {d \ mathbf {m}} {dt}} = \ gamma \ mathbf {m} \ razy \ mathbf {B} + \ mathbf {B } _ {1}}$ Łatwiej jest go rozwiązać, przekształcając układ współrzędnych na OXYZ, w którym staje się osią OX, w tym układzie - ${\ Displaystyle \ mathbf {B} _ {1}}$ ${\ Displaystyle {\ Frac {d \ mathbf {m} '} {dt}} = {\ Frac {d \ mathbf {m}} {dt}} + \mathbf {m} \times {\boldsymbol {\omega}}}$ tutaj i $\$$\ Displaystyle \ omega _$${\ Displaystyle \ omega _ {1} = \ gamma B_ {1}}$ B i widać, że- ${\ Displaystyle {\ Frac {d \ mathbf {m} '} {dt}} = \ mathbf {m } \times ({\boldsymbol {\omega}}_{0}+{\boldsymbol {\omega}}_{1}-{\boldsymbol {\omega}})=\mathbf {m} \times (\Delta {\boldsymbol {\omega}}+{\boldsymbol {\omega}}_{1})}$ więc tutaj skuteczne pole staje się : ${\ Displaystyle \ mathbf {B} _ {\ rm {skuteczne}} = \Delta {\boldsymbol {\omega}}-{\boldsymbol {\omega _{1}}}=\Delta \omega {\hat {z}}-\omega _{1}{\hat {X}}}$

Więc kiedy $momentu$ wysoka amplituda precesji pozwala na całkowite odwrócenie Przewidywania mechaniki klasycznej i mechaniki kwantowej dobrze ze sobą korespondują, co można postrzegać jako przykład zasady zgodności Bohra , która mówi, że zjawiska mechaniki kwantowej, gdy są przewidywane w systemie klasycznym, powinny odpowiadać klasycznemu wynikowi. Źródłem tej zgodności jest to, że ewolucja oczekiwanej wartości momentu magnetycznego jest identyczna z ewolucją otrzymaną w rozumowaniu klasycznym. Wartość oczekiwana momentu magnetycznego wynosi ${\ Displaystyle \ langle \ mathbf {m} \ rangle = \ gamma \ langle \ mathbf {S} \ rangle}$ . Ewolucja w czasie ${\ Displaystyle \ langle \ mathbf {m} \ rangle}$ jest podana przez

       
               ${\ Displaystyle i \ hbar {\ Frac {d} {dt}} \ langle \ mathbf {m} \ rangle = \ langle [\ mathbf {m } , {\ kapelusz {H}}] \ rangle }$${\ Displaystyle {\ kapelusz {H}} = - \ mathbf {m} \ cdot \ mathbf {B} (t) }$

więc ${\ Displaystyle [m_ {i}, {\ kapelusz {H}}] = [m_ {i}, -m_ {j} B_ {j} ]=[\gamma \mathbf {S} _{i},-\gamma \mathbf {S} _{j}\mathbf {B} _{j}]=-\gamma ^{2}[\mathbf {S } _{i},\mathbf {S} _{j}\mathbf {B} _{j}]=-\gamma ^{2}i\hbar [{\mathbf {S} _{k}\mathbf { B} _{j}-\mathbf {S} _{j}\mathbf {B} _{k}}],(i\neq j,k)}$

Więc ${\ Displaystyle [m_ {i}, {\ kapelusz {H}}] = i \ hbar \ gamma [\ mathbf {B} _{j}\mathbf {m} _{k}-\mathbf {B} _{k}\mathbf {m} _{j}]}$ i

${\ Displaystyle {\ Frac {d} {dt}} \ langle \ mathbf {m} (t) \ rangle = \gamma \langle \mathbf {m} (t)\rangle \times \langle \mathbf {B} (t)\rangle }$

co wygląda dokładnie podobnie do równania ruchu momentu magnetycznego w mechanice klasycznej - ${\ displaystyle \ mathbf {m}}$

                  $\ Displaystyle {\ Frac {d} {dt}} \ mathbf {m} (t) = \ gamma \ mathbf {m} (t) \times \mathbf {B} (t)}$ 

Ta analogia w matematycznym równaniu ewolucji momentu magnetycznego i jego wartości oczekiwanej ułatwia zrozumienie zjawiska bez znajomości mechaniki kwantowej.

Rezonans magnetyczny

Zobacz też: Rezonans magnetyczny

W obrazowaniu metodą rezonansu magnetycznego (MRI) wykorzystuje się spinowy moment pędu protonu. Najbardziej dostępnym źródłem protonów w ludzkim ciele są atomy wodoru w wodzie. Silne pole magnetyczne $wody$ powoduje pojawienie się dwóch różnych poziomów energii dla wirowania momentu pędu i ${\ displaystyle + \ gamma \ hbar B/2}$ i ${\ Displaystyle - \ gamma \ hbar B/2}$ , używając ${\ Displaystyle E = - \ mathbf {\ mu} \ cdot \ mathbf {B}}$ .

Zgodnie z rozkładem Boltzmanna , ponieważ liczba systemów posiadających energię $\ Displaystyle$ N $N_ {0}}$${\ displaystyle N_ {0} e ^ {- E / kT}}$ temperaturze wynosi ${\ displaystyle T}$ (gdzie $Boltzmanna$ stałą ) , niższy poziom energii, związany z wirowaniem ${\ Displaystyle \ hbar / 2}$ , jest bardziej zaludniony niż drugi. W obecności wirującego pola magnetycznego więcej protonów odwraca się od ${\ Displaystyle S_ {z} = + \ hbar /2}$ do ${\ Displaystyle S_ {z} = - \hbar /2}$ niż w drugą stronę, powodując absorpcję promieniowania mikrofalowego lub radiowego (z pola wirującego). Kiedy pole jest wycofane, protony mają tendencję do ponownego równoważenia się wzdłuż rozkładu Boltzmanna, więc niektóre z nich przechodzą z wyższych poziomów energii na niższe, emitując promieniowanie mikrofalowe lub fale radiowe o określonych częstotliwościach.

elektronowy rezonans paramagnetyczny ) wykorzystuje się spinowy moment pędu niesparowanych elektronów w celu wykrycia wolnych rodników itp.

Rezonans magnetyczny jako zjawisko kwantowe

Zjawisko rezonansu magnetycznego jest zakorzenione w istnieniu spinowego momentu pędu układu kwantowego i jego określonej orientacji względem przyłożonego pola magnetycznego. Oba przypadki nie mają wyjaśnienia w podejściu klasycznym i można je zrozumieć jedynie za pomocą mechaniki kwantowej. Niektórzy twierdzą, że zjawiska czysto kwantowe to takie, których nie można wyjaśnić podejściem klasycznym. Na przykład zjawiska w domenie mikroskopowej, które można do pewnego stopnia opisać za pomocą klasycznej analogii, nie są tak naprawdę zjawiskami kwantowymi. Ponieważ podstawowe elementy rezonansu magnetycznego nie mają klasycznego pochodzenia, chociaż można dokonać analogii z klasyczną precesją Larmora , MR należy traktować jako zjawisko kwantowe.

Zobacz też

• Magnetyczny rezonans jądrowy
• Rezonans magnetyczny
• Równania Blocha
• Fizyka rezonansu magnetycznego

• Feynman, Leighton, Sands. Wykłady Feynmana z fizyki, tom 3 . {{ cite book }} : CS1 maint: wiele nazwisk: lista autorów ( link )
• Cohen-Tannoudji Claude. Mechanika kwantowa . Wiley-VCH.
• Griffiths David J. Wprowadzenie do mechaniki kwantowej . Edukacja Pearson, Inc.