Częstotliwość Rabi to częstotliwość, przy której amplitudy prawdopodobieństwa dwóch poziomów energii atomowej zmieniają się w oscylującym polu elektromagnetycznym. Jest proporcjonalny do momentu dipolowego przejścia dwóch poziomów i do amplitudy ( nie natężenia ) pola elektromagnetycznego . Przemieszczanie się populacji pomiędzy poziomami takiego 2-poziomowego systemu oświetlonego światłem dokładnie rezonującym z różnicą energii między dwoma poziomami będzie następować z częstotliwością Rabi; kiedy padające światło jest odstrojone od tej różnicy energii (odstrojone od rezonansu), wówczas transfer populacji następuje przy uogólnionej częstotliwości Rabi . Częstotliwość Rabi jest pojęciem półklasycznym, ponieważ traktuje atom jako obiekt o skwantowanych poziomach energii , a pole elektromagnetyczne jako falę ciągłą.
W kontekście eksperymentu z jądrowym rezonansem magnetycznym częstotliwość Rabiego to częstotliwość nutacji wektora magnetyzacji jądrowej netto próbki wokół pola o częstotliwości radiowej. (Zauważ, że różni się to od częstotliwości Larmora , która charakteryzuje precesję poprzecznego namagnesowania jądrowego wokół statycznego pola magnetycznego).
Pochodzenie
Rozważ dwa stany własne energii układu kwantowego z hamiltonianem 
 może to być hamiltonian cząstki w potencjał, jak atom wodoru lub atomy metali alkalicznych):
może to być hamiltonian cząstki w potencjał, jak atom wodoru lub atomy metali alkalicznych):

Chcemy rozważyć hamiltonian zależny od czasu

gdzie  to potencjał pola elektromagnetycznego. Traktując potencjał jako perturbację , możemy oczekiwać, że stany własne zaburzonego hamiltonianu będą pewną mieszanką stanów własnych pierwotnego hamiltonianu ze współczynnikami zależnymi od czasu:
to potencjał pola elektromagnetycznego. Traktując potencjał jako perturbację , możemy oczekiwać, że stany własne zaburzonego hamiltonianu będą pewną mieszanką stanów własnych pierwotnego hamiltonianu ze współczynnikami zależnymi od czasu:

Podstawiając to do zależnego od czasu równania Schrödingera

biorąc iloczyn wewnętrzny z każdym z  i
i  i używając warunku ortogonalności stanów własnych
i używając warunku ortogonalności stanów własnych  do
do  i
i  }
}

gdzie  . Dwa terminy w nawiasach to elementy matrycy dipolowej rozmieszczone w wektorze polaryzacji pola elektromagnetycznego. Rozważając sferycznie symetryczne przestrzenne funkcje własne
. Dwa terminy w nawiasach to elementy matrycy dipolowej rozmieszczone w wektorze polaryzacji pola elektromagnetycznego. Rozważając sferycznie symetryczne przestrzenne funkcje własne  potencjału atomu wodoru , diagonalne elementy macierzy dążą do zera, pozostawiając nas z
potencjału atomu wodoru , diagonalne elementy macierzy dążą do zera, pozostawiając nas z

Lub

Tutaj  , gdzie
, gdzie  to częstotliwość Rabiego.
to częstotliwość Rabiego.
Intuicja
W liczniku mamy przejściowy moment dipolowy dla 
 kwadratowa amplituda reprezentuje siłę oddziaływania między polem elektromagnetycznym a atomem i to wektorowa amplituda pola elektrycznego , która obejmuje polaryzację . Licznik ma wymiary energii, więc dzielenie przez
kwadratowa amplituda reprezentuje siłę oddziaływania między polem elektromagnetycznym a atomem i to wektorowa amplituda pola elektrycznego , która obejmuje polaryzację . Licznik ma wymiary energii, więc dzielenie przez  daje częstotliwość kątową .
daje częstotliwość kątową .
Przez analogię z klasycznym dipolem jasne jest, że atom o dużym momencie dipolowym będzie bardziej podatny na zakłócenia wywołane polem elektrycznym . Iloczyn skalarny obejmuje współczynnik , gdzie  między polaryzacją światła a
między polaryzacją światła a  Kiedy są równoległe, interakcja jest najsilniejsza, gdy są prostopadłe, w ogóle nie ma interakcji.
Kiedy są równoległe, interakcja jest najsilniejsza, gdy są prostopadłe, w ogóle nie ma interakcji.
Jeśli przepiszemy równania różniczkowe znalezione powyżej:

i zastosuj przybliżenie fali wirującej , które zakłada, że  , tak że możemy odrzucić mamy warunki oscylacyjne o wysokiej częstotliwości
, tak że możemy odrzucić mamy warunki oscylacyjne o wysokiej częstotliwości

gdzie  . Możemy rozwiązać te równania, zakładając, że w
. Możemy rozwiązać te równania, zakładając, że w  w
w  znaleźć (tj. do
znaleźć (tj. do 

Jest to prawdopodobieństwo jako funkcja rozstrojenia i czasu populacji stanu  . Wykres jako funkcja rozstrojenia i zmiany czasu od 0 do
. Wykres jako funkcja rozstrojenia i zmiany czasu od 0 do  daje:
daje:
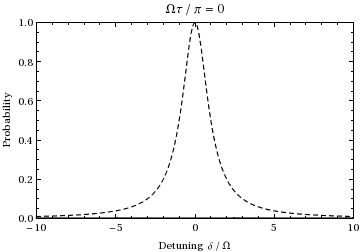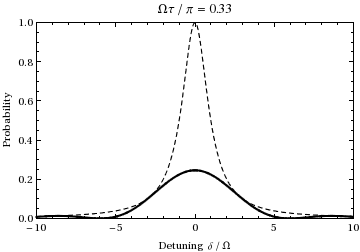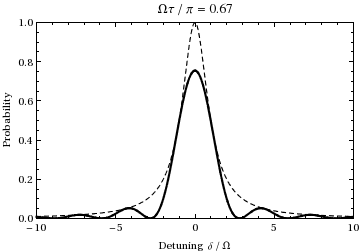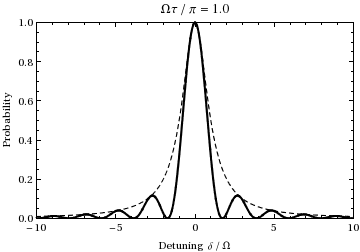
Widzimy, że dla  populacja będzie oscylować między dwoma stanami z częstotliwością Rabi.
populacja będzie oscylować między dwoma stanami z częstotliwością Rabi.
Uogólniona częstotliwość Rabi
Ilość  określana jako „uogólniona W przypadkach, w których flopowanie Rabi faktycznie występuje przy tej częstotliwości, gdzie jest rozstrojeniem
określana jako „uogólniona W przypadkach, w których flopowanie Rabi faktycznie występuje przy tej częstotliwości, gdzie jest rozstrojeniem 
 , miara tego, jak daleko światło jest poza rezonansem w stosunku do przejścia. Na przykład, badając powyższą animację przy częstotliwości przesunięcia ± 1,73, można zobaczyć, że podczas cyklu 1/2 Rabi (w rezonansie) pokazanego podczas animacji, oscylacja zamiast tego przechodzi jeden pełny cykl, a więc dwukrotnie ( normalnie ) częstotliwość Rabi
, miara tego, jak daleko światło jest poza rezonansem w stosunku do przejścia. Na przykład, badając powyższą animację przy częstotliwości przesunięcia ± 1,73, można zobaczyć, że podczas cyklu 1/2 Rabi (w rezonansie) pokazanego podczas animacji, oscylacja zamiast tego przechodzi jeden pełny cykl, a więc dwukrotnie ( normalnie ) częstotliwość Rabi  , tak jak przewiduje to równanie. Należy również zauważyć, że gdy częstotliwość padającego światła przesuwa się dalej od częstotliwości przejściowej, amplituda oscylacji Rabi maleje, co ilustruje przerywana obwiednia na powyższym wykresie.
, tak jak przewiduje to równanie. Należy również zauważyć, że gdy częstotliwość padającego światła przesuwa się dalej od częstotliwości przejściowej, amplituda oscylacji Rabi maleje, co ilustruje przerywana obwiednia na powyższym wykresie.
Dwufotonowa częstotliwość Rabi
Spójne oscylacje Rabiego mogą być również napędzane przez przejścia dwufotonowe . W tym przypadku rozważamy układ z trzema poziomami energii atomowej,  ,
,  i
i  , gdzie
, gdzie  reprezentuje tak zwany stan pośredni z odpowiednią częstotliwością
reprezentuje tak zwany stan pośredni z odpowiednią częstotliwością  oraz pole elektromagnetyczne o dwóch składowych częstotliwości:
oraz pole elektromagnetyczne o dwóch składowych częstotliwości:

Teraz  może być znacznie większy niż zarówno
może być znacznie większy niż zarówno  jak i
jak i  lub
lub  , jak pokazano na rysunku po prawej stronie.
, jak pokazano na rysunku po prawej stronie.

Schemat wzbudzenia dwufotonowego.

jest pokazany po lewej stronie, podczas gdy

jest pokazany po prawej stronie. Oś pionowa to oś częstotliwości (lub energii).
Przejście dwufotonowe to nie to samo, co wzbudzenie ze stanu podstawowego do stanu pośredniego, a następnie ze stanu pośredniego do stanu wzbudzonego. Zamiast tego atom pochłania jednocześnie dwa fotony i jest promowany bezpośrednio między stanem początkowym i końcowym. Istnieją dwa warunki konieczne, aby ten proces dwufotonowy (znany również jako proces ramanowski) był dominującym modelem interakcji światło-materia:

Innymi słowy, suma częstotliwości dwóch fotonów musi być w rezonansie z przejściem między stanem początkowym i końcowym, a poszczególne częstotliwości fotonów muszą być rozstrojone od stanu pośredniego do przejścia stanu początkowego i końcowego. Jeśli  ostatni warunek nie zostanie spełniony i dominującym procesem będzie proces rządzony przez równania szybkości, w których stan pośredni jest wypełniony i stymulowany, a zdarzenia emisji z tego stanu zapobiegają możliwości napędzanie spójnych oscylacji między stanem początkowym i końcowym.
ostatni warunek nie zostanie spełniony i dominującym procesem będzie proces rządzony przez równania szybkości, w których stan pośredni jest wypełniony i stymulowany, a zdarzenia emisji z tego stanu zapobiegają możliwości napędzanie spójnych oscylacji między stanem początkowym i końcowym.
Możemy wyprowadzić dwufotonową częstotliwość Rabiego, wracając do równań

które teraz opisują wzbudzenie między stanem podstawowym a stanem pośrednim. Wiemy, że mamy rozwiązanie

gdzie  uogólnioną częstotliwością Rabi dla przejścia ze stanu początkowego Podobnie dla przejścia ze stanu pośredniego do końcowego mamy równania
uogólnioną częstotliwością Rabi dla przejścia ze stanu początkowego Podobnie dla przejścia ze stanu pośredniego do końcowego mamy równania

teraz podstawiamy do  równania dla
równania dla 

Takie, że po rozwiązaniu tego równania stwierdzamy, że współczynnik jest proporcjonalny do:

Jest to efektywna lub dwufotonowa częstotliwość Rabi. Jest to iloczyn poszczególnych częstotliwości Rabi dla  i
i  , podzielone przez rozstrojenie ze stanu pośredniego
, podzielone przez rozstrojenie ze stanu pośredniego  .
.
Zobacz też


























































