Samolot Benza

W matematyce płaszczyzna Benza jest rodzajem dwuwymiarowej struktury geometrycznej , nazwanej na cześć niemieckiego matematyka Waltera Benza . Termin ten został zastosowany do grupy obiektów, które powstają ze wspólnej aksjomatyzacji pewnych struktur i dzielą się na trzy rodziny, które zostały wprowadzone oddzielnie: płaszczyzny Möbiusa , płaszczyzny Laguerre'a i płaszczyzny Minkowskiego .

Samolot Möbiusa

Klasyczny samolot Möbiusa: model 2d/3d

Rozpoczęcie od rzeczywistej płaszczyzny euklidesowej i połączenie zestawu linii ze zbiorem okręgów w celu utworzenia zestawu bloków skutkuje niejednorodną strukturą padania : trzy różne punkty określają jeden blok, ale linie są rozróżnialne jako zbiór bloków, które parami się wzajemnie przecinają w jednym punkcie bez bycia stycznym (lub bez punktów, gdy są równoległe). Dodanie do zestawu punktów nowego punktu $linii,$ powoduje, że każdy blok jest określony przez dokładnie trzy punkty, a także przecięcie dowolnych dwóch bloków według jednolitego wzoru (przecinające się w dwóch punkty styczne lub nieprzecinające się). Ta jednorodna geometria nazywana jest klasyczną geometrią odwrotną lub płaszczyzną Möbiusa. Niejednorodność opisu (linie, okręgi, nowy punkt) może zostać uznana za niemerytoryczną przy użyciu trójwymiarowego modelu. Używając rzutu stereograficznego , można zobaczyć, że klasyczna płaszczyzna Möbiusa jest izomorficzna z geometrią płaskich przekrojów (okręgów) na kuli w euklidesowej przestrzeni 3.

Analogicznie do (aksjomatycznej) płaszczyzny rzutowej , płaszczyzna (aksjomatyczna) Möbiusa definiuje strukturę incydencji. Płaszczyzny Möbiusa można podobnie konstruować na polach innych niż liczby rzeczywiste.

Samolot Laguerre'a

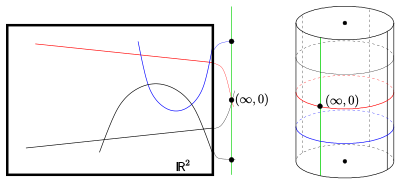
klasyczna płaszczyzna Laguerre'a: model 2d/3d

Zaczynając ponownie od $biorąc$ ${\ Displaystyle y = ax ^ {2} + bx + c } ($ za pomocą równań ${\ Displaystyle (\ infty, a)}$ $bloki ,$ następująca homogenizacja nowy . Stąd zbiór punktów to ${\ Displaystyle (\ mathbb {R} \ kubek {\ infty}) \ razy \ mathbb {R}}$ . Ta geometria paraboli nazywana jest klasyczną płaszczyzną Laguerre'a (pierwotnie została zaprojektowana jako geometria zorientowanych linii i okręgów. Obie geometrie są izomorficzne).

$)$ Möbiusa, istnieje trójwymiarowy model: geometria eliptycznych odcinków płaszczyzny na ortogonalnym cylindrze ( . Abstrakcja prowadzi (analogicznie do płaszczyzny Möbiusa) do aksjomatycznej płaszczyzny Laguerre'a.

Samolot Minkowskiego

klasyczna płaszczyzna Minkowskiego: model 2d/3d

${\ Displaystyle y = {\ tfrac {a} {xb}} + c, a \ neq 0}$ od i łącząc linie $\$ $Displaystyle \ mathbb {$ w celu uzyskania zestawu bloków następujący pomysł ujednolica strukturę występowania: Dodaj do dowolnej linii punkt ${\ Displaystyle (\ infty, \ infty)}$ i do dowolnej hiperboli ${\ Displaystyle y = {\ tfrac {a} {xb}} + c, a \ neq 0}$ dwa punkty ${\ Displaystyle (b, \ infty), (\ infty, c)}$ . Stąd zestaw punktów to ${\ Displaystyle (\ mathbb {R} \ cup \ {\ infty \}) ^ {2}}$ . Ta geometria hiperboli nazywana jest klasyczną płaszczyzną Minkowskiego.

Analogicznie do klasycznych płaszczyzn Möbiusa i Laguerre'a istnieje trójwymiarowy model: klasyczna płaszczyzna Minkowskiego jest izomorficzna z geometrią płaskich przekrojów hiperboloidy jednego arkusza (niezdegenerowana kwadryka o indeksie 2) w trójwymiarowej przestrzeni rzutowej . Podobnie jak w dwóch pierwszych przypadkach otrzymujemy płaszczyznę (aksjomatyczną) Minkowskiego.

Płaskie geometrie okręgów lub płaszczyzny Benza

Ze względu na zasadniczą rolę koła (uważanego za niezdegenerowany stożek w płaszczyźnie rzutowej ) i opis płaszczyzny oryginalnych modeli, trzy typy geometrii są zaliczane do płaskich geometrii okręgu lub na cześć Waltera Benza, który uważał te struktury geometryczne ze wspólnego punktu widzenia, płaszczyzny Benza.

Zobacz też

Francis Buekenhout (1981) „Plany Benza”, Journal of Geometry 17 (1): 61–8.

Linki zewnętrzne