Samolot Laguerre'a

W matematyce płaszczyzna Laguerre'a jest jednym z trzech typów płaszczyzn Benza , którymi są płaszczyzna Möbiusa , płaszczyzna Laguerre'a i płaszczyzna Minkowskiego . Płaszczyzny Laguerre'a zostały nazwane na cześć francuskiego matematyka Edmonda Nicolasa Laguerre'a .

klasyczna płaszczyzna Laguerre'a: model 2d/3d

Klasyczna płaszczyzna Laguerre'a to $parabol$ , która padania krzywych, w płaszczyzna afiniczna . Aby $_$ _ ${\ Displaystyle (\ infty, a)}$ . Kolejną zaletą tego uzupełnienia jest to, że płaska geometria ukończonych parabol/linii jest izomorficzna z geometrią płaskich przekrojów walca (patrz poniżej).

Klasyczny prawdziwy samolot Laguerre'a

Pierwotnie klasyczna płaszczyzna Laguerre'a była definiowana jako geometria zorientowanych linii i okręgów w rzeczywistej płaszczyźnie euklidesowej (patrz ). Tutaj preferujemy paraboliczny model klasycznej płaszczyzny Laguerre'a.

definiujemy:

${\ Displaystyle {\ mathcal {P}}: = \ mathbb {R} ^ {2} \ kubek (\ {\ infty \} \ razy \mathbb {R} ),\ \infty \notin \mathbb {R} ,}$ zbiór punktów , ${\ Displaystyle {\ mathcal {Z}}: = \ {\ {(x, y) \ w \ mathbb {R} ^ {2 }\mid y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\mid a,b,c\in \mathbb {R} \}}$ zbiór cykli .

Struktura $_$ _ _ _

$plus$ punktów to kopia (patrz $.$ Każda parabola / linia ${\ Displaystyle y = ax ^ {2} + bx + c}$ otrzymuje dodatkowy punkt ${\ Displaystyle (\ infty, a)}$ .

Punkty o tej samej współrzędnej x nie mogą być połączone krzywymi ${\ Displaystyle y = ax ^ {2} + bx + c}$ . Stąd definiujemy:

$)$ punkty są równoległe ( jeśli ${\ Displaystyle A$$= B}$ lub nie ma cyklu zawierającego $}$ i ${\ Displaystyle B}$ .

Do opisu klasycznej rzeczywistej płaszczyzny Laguerre'a powyżej dwóch punktów $\ Displaystyle (a_ {1}, a_ {2}), (b_ {1}, b_ { 2})}$ są równoległe wtedy i tylko wtedy, gdy ${\ Displaystyle a_ {1} = b_ {1}}$ . ${\ Displaystyle \ równoległy}$ jest relacją równoważności , podobną do równoległości linii.

Struktura częstości występowania ma następujące właściwości: ${\ Displaystyle ({\ mathcal {P}}, {\ mathcal {Z}}, \ in)$

Lemat:

• Dla dowolnych trzech punktów parami nie równoległych istnieje dokładnie jeden cykl $b ,$$,$$A$ .
• Dla dowolnego punktu $Displaystyle$ dowolnego cyklu istnieje dokładnie jeden punkt $P '\ w z}$${\$ taki, że $Displaystyle P \ równoległy P ' }$ .
• $z$ dowolnego cyklu $\ notin z}$ dowolnego punktu i dowolnego punktu , który nie jest równoległy do $\ Displaystyle P \ in z },$ jest ${\ Displaystyle Q$ dokładnie jeden cykl ${\ Displaystyle Z'}$ do ${\ Displaystyle P, Q}$ z $}$$\ {P \}}$ , tj ${\ displaystyle z}$ stykają się ze sobą oo i ${\ displaystyle z'$ .

Płaszczyzna Laguerre'a: rzut stereograficzny płaszczyzny xz na cylinder

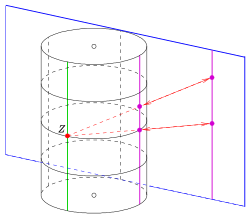
Podobnie do sferycznego modelu klasycznej płaszczyzny Moebiusa istnieje model walcowy dla klasycznej płaszczyzny Laguerre'a:

${\ Displaystyle ({\ mathcal {P}}, {\ mathcal {Z}}, \ in)}$ jest izomorficzne z geometrią płaskich przekrojów okrągłego walca w ${\ Displaystyle \ mathbb {R} ^{3}}$ .

Poniższe odwzorowanie $rzutem$ ze środkiem ${\ Displaystyle (0,1,0)}$ , który odwzorowuje płaszczyznę xz na cylinder za pomocą równania ${\ Displaystyle u ^ {2} + v ^ {2} -v = 0}$ , oś ${\ Displaystyle (0, {\ tfrac {1} {2}}, ..) }$ i promień ${\ displaystyle r = {\ tfrac {1} {2}} \:}$

${\ Displaystyle \ Phi: \ (x, z) \ rightarrow ({\ Frac {x} {1 + x ^ {2}}}, {\ Frac {x ^ {2}} {1 + x ^ {2} }},{\frac {z}{1+x^{2}}})=(u,v,w)\ .}$

• Punkty $($ linia na cylindrze przechodząca przez środek)
• ${\ Displaystyle \ Phi}$ rzutuje parabolę / linię z równaniem ${\ Displaystyle z = ax ^ {2} + bx + c}$ na płaszczyznę ${\ Displaystyle wa = bu + (ac) (v-1)}$ . Tak więc obraz paraboli / linii jest płaskim przekrojem cylindra z nieprostopadłą płaszczyzną, a zatem okręgiem / elipsą bez punktu ${\ Displaystyle (0,1, a)}$ . Parabole / $poziome$ )
• Linia ( a = 0) jest odwzorowywana na okrąg / elipsę przechodzącą przez środek $i$$Displaystyle (0,1,0)}$ parabolę ( ) na okrąg / elipsa, które nie zawierają ${\ Displaystyle (0,1,0)}$ .

Aksjomaty płaszczyzny Laguerre'a

Powyższy Lemat prowadzi do następującej definicji:

Niech ${\ Displaystyle {\ mathcal {L}}: = ({\ mathcal {P}}, {\ mathcal {Z}}, \ in)} będzie$ strukturą częstości z punktem zestaw i zestaw cykli $\ Displaystyle {\ mathcal {Z}}$${$ . $Displaystyle A$ punkty są równoległe ( $równoległy B} )$ jeśli
${\ displaystyle A = B}$ lub nie ma cyklu zawierającego $displaystyle$ b $A}$ . nazywa się płaszczyzną Laguerre'a , jeśli zachodzą następujące aksjomaty: ${\ displaystyle {\ mathcal {L}}}$

Płaszczyzna Laguerre'a: aksjomaty

B1: Dla dowolnych trzech punktów ${$$B, C}$ równoległych istnieje dokładnie jeden cykl, $A$ b .

$P}$ : Dla dowolnego punktu ${$ dowolnego cyklu $P.$ dokładnie jeden punkt , że ${\ Displaystyle P \ równoległy P '}$ .

B3: $in$ dowolnego cyklu , dowolnego punktu i dowolnego punktu , który nie jest równoległy do $\$$P$$}$ jest dokładnie jeden cykl z $\ Displaystyle Z'}$ do ${\ Displaystyle P, Q}$${\ Displaystyle Z \ nasadka z '= \ {P \}}$ ,

tj $\ Displaystyle Z}$${$ i stykają się ze sobą w $\ Displaystyle P}$ .

B4: Każdy cykl zawiera co najmniej trzy punkty. Istnieje co najmniej jeden cykl. Istnieją co najmniej cztery punkty, które nie należą do cyklu.

$do$ punkty koncykliczne $A$ cykl $Displaystyle$ z \ .

Z definicji relacji i aksjomatu B2 otrzymujemy ${\ displaystyle \ równoległy}$

Lemat : Relacja $równoważności$ relacją .

Wzorując się na cylindrycznym modelu klasycznej płaszczyzny Laguerre'a, wprowadzamy oznaczenie:

a) dla ${\ Displaystyle P \ w {\ mathcal {P}}}$ ustawiamy ${\ Displaystyle {\ overline {P}}: = \ {Q \ w {\ mathcal {P}} \ |\ P \ równoległy Q \}}$ . b) Klasa równoważności nazywa się generatorem . ${\ displaystyle {\ overline {P}}}$

Dla klasycznej płaszczyzny Laguerre'a generatorem jest linia równoległa do osi y (model płaski) lub linia na cylindrze (model przestrzenny).

Związek z geometrią liniową określa następująca definicja:

L ${\ Displaystyle {\ mathcal {L}}: = ({\ mathcal {P}}, {\ mathcal {Z}}, \ in)$ } struktura lokalna

${\ Displaystyle {\ mathcal {A}} _ {P}: = ({\ mathcal {P}} \ setminus \ {{\ overline {P}} \}, \ {z \ setminus \ {{\ overline {P }}\}\ |\ P\in z\in {\mathcal {Z}}\}\cup \{{\overline {Q}}\ |\ Q\in {\mathcal {P}}\setminus \{ {\overline {P}}\},\w )}$

i nazwijmy to resztą w punkcie P.

$}$ płaszczyzny klasycznej płaszczyzny Laguerre'a prawdziwa płaszczyzna afiniczna jest $} _ {\ infty}$ . Generalnie dostajemy

Twierdzenie: Każda reszta płaszczyzny Laguerre'a jest płaszczyzną afiniczną .

I równoważna definicja płaszczyzny Laguerre'a:

${\ displaystyle {\ mathcal {A}} _ {P}}$ : Struktura incydencji wraz $na$ relacją równoważności jest $A$ Laguerre'a wtedy i tylko wtedy, gdy dla $dowolnego$ punktu jest płaszczyzną afiniczną.

Skończone płaszczyzny Laguerre'a

minimalny model płaszczyzny Laguerre'a (pokazano tylko 4 z 8 cykli)

Następująca struktura częstości jest „minimalnym modelem” płaszczyzny Laguerre'a:

${\ Displaystyle {\ mathcal {P}}: = \ {A_ {1}, A_ {2}, B_ {1 },B_{2},C_{1},C_{2}\}\,}$

${\ Displaystyle {\ mathcal {Z}}: = \ {\ {A_ {i}, B_ {j}, C_ {k} \} \ |\ i, j, k = 1,2 \} \,}$

${\ Displaystyle A_ {1} \ równoległy A_ {2}, \ B_ {1} \ równoległy B_ {2}, \ C_ {1} \ równoległy C_ {2} \ .}$

Stąd ${\ Displaystyle | {\ mathcal {P}} | = 6}$ i ${\ Displaystyle | {\ mathcal {Z}} | = 8 \ .}$

Dla skończonych płaszczyzn Laguerre'a, tj ${\ Displaystyle | {\ mathcal {P}} | <\ infty}$ , otrzymujemy:

$,$ : Dla $_$${\ Displaystyle {\ mathcal {L}}: = ({\ mathcal {P}}, {\ mathcal {Z}}, \ w)} mamy$ dowolnego skończonej płaszczyzny L :

${\ Displaystyle | z_ {1} | = | z_ {2} | = | {\ overline {P}} | +1}$ .

$_$ płaszczyzny _ cykl ${\ Displaystyle Z \ w {\ mathcal {Z}}}$ liczba całkowita ${\ Displaystyle n: = | z | -1}$ nazywa się rzędem ${\ displaystyle {\ mathcal {L}}}$ .

Z kombinatoryki otrzymujemy

Lemat: Niech ${\ Displaystyle {\ mathcal {L}}: = ({\ mathcal {P}}, {\ mathcal {Z}}, \ in)} będzie$ Laguerre— płaszczyzna porządku ${\ displaystyle n}$ . Następnie

${\ displaystyle n \ quad,}$ ) dowolna reszta $n$ afiniczną rzędu b) ${\ Displaystyle | {\ mathcal {P}} | = n ^ {2} + n,}$ do) ${\ Displaystyle | {\ mathcal {Z}} | = n ^ {3}.}$

Samoloty Miquelian Laguerre

$zawsze$ formalne uogólnienie klasycznego modelu płaszczyzny Laguerre'a, tj. zastąpienie dowolnym polem $,$ prowadzi do przykładu płaszczyzny Laguerre'a

Twierdzenie: dla pola i ${\ displaystyle K}$

${\ Displaystyle {\ mathcal {P}}: = K ^ {2} \ kubek}$${\ Displaystyle (\ {\ infty \} \ razy K. ),\ \infty \notin K}$ ,

${\ Displaystyle {\ mathcal {Z}}: = \ {\ {(x, y) \ w K ^ {2} \ |\ y = ax ^ {2} + bx + c \}\ puchar \ {(\ infty, a) \} \ |\ a, b, c \ w K \}}$ struktura występowania

${\ Displaystyle {\ mathcal {L}}(K):=({\mathcal {P}},{\mathcal {Z}},\in )} jest płaszczyzną Laguerre'a o$ następującej relacji równoległej: ${\ Displaystyle (a_ {1}, a_ {2}) \ równolegle (b_ {1}, b_ {2})}$ wtedy i tylko wtedy, gdy ${\ styl wyświetlania a_{1}=b_{1}}$ .

Podobnie jak płaszczyzna Möbiusa, wersja Laguerre'a twierdzenia Miquela zawiera:

Twierdzenie Miquela (okręgi narysowane zamiast parabol)

Twierdzenie Miquela: dla płaszczyzny Laguerre'a prawdziwe jest: ${\ Displaystyle {\ mathcal {L}} (K)}$

Jeśli dla dowolnych 8 parami nierównoległych punktów, które można przypisać wierzchołkom sześcianu tak, że punkty na 5 ścianach odpowiadają ${\ Displaystyle P_ {1}, \ ldots, P_ {8}}$ koncykliczne poczwórne, to szósta poczwórna liczba punktów jest również koncykliczna.

(Dla lepszego widoku na rysunku zamiast paraboli narysowano okręgi)

Znaczenie twierdzenia Miquela pokazuje następujące twierdzenie, które zawdzięczamy vd Waerdenowi, Smidowi i Chenowi:

$.$ : Tylko płaszczyzna twierdzenie

Ze względu na ostatnie twierdzenie nazywa się „ $.$

Minimalny model płaszczyzny Laguerre'a to miquelian. Jest izomorficzny z płaszczyzną Laguerre'a z ( $\$$} \displaystyle\{0,1\}}$${\ mathcal {L}}$ ( ).

Odpowiedni rzut stereograficzny $jest$ , że $izomorficzny z$ płaskich przekrojów kwadratowego .

Jajowate płaszczyzny Laguerre'a

Istnieje wiele samolotów Laguerre, które nie są miquelianami (patrz link poniżej). Klasą najbardziej zbliżoną do miqueliańskich płaszczyzn Laguerre'a są owalne płaszczyzny Laguerre'a . Jajowata płaszczyzna Laguerre'a to geometria płaskich przekrojów cylindra, który jest zbudowany przy użyciu owalu zamiast niezdegenerowanego stożka. Owal jest zbiorem kwadratowym i ma te same właściwości geometryczne, co niezdegenerowany stożek na płaszczyźnie rzutowej: 1) linia przecina owal w zera, jednym lub dwóch punktach oraz 2) w dowolnym punkcie istnieje unikalna styczna. Prosty owal w rzeczywistej płaszczyźnie można zbudować, sklejając ze sobą dwie odpowiednie połówki różnych elips, tak aby wynik nie był stożkiem. Nawet w skończonym przypadku istnieją owale (patrz zbiór kwadratowy ).

Zobacz też

• Transformacje Laguerre'a

Linki zewnętrzne

• Samolot Benz w Encyklopedii Matematyki
• Notatka z wykładu Płaskie geometrie okręgów , wprowadzenie do płaszczyzn Moebiusa, Laguerre'a i Minkowskiego, s. 67