Sekwencja o maksymalnej długości

Sekwencja o maksymalnej długości ( MLS ) to rodzaj pseudolosowej sekwencji binarnej .

Są to sekwencje bitów generowane przy użyciu rejestrów przesuwnych z maksymalnym liniowym sprzężeniem zwrotnym i są tak zwane, ponieważ są okresowe i odtwarzają każdą sekwencję binarną (z wyjątkiem wektora zerowego), która może być reprezentowana przez rejestry przesuwne ( tj . ciąg o długości 2 ^m − 1). MLS jest czasami nazywany n-sekwencją lub m-sekwencją . MLS są widmowo płaskie , z wyjątkiem prawie zerowego składnika DC.

Ciągi te można przedstawić jako współczynniki wielomianów nierozkładalnych w pierścieniu wielomianowym nad Z/2Z .

Praktyczne zastosowania MLS obejmują pomiar odpowiedzi impulsowych (np. pogłosu w pomieszczeniu lub czasów nadejścia z holowanych źródeł w oceanie). Są również wykorzystywane jako podstawa do wyprowadzania sekwencji pseudolosowych w cyfrowych systemach komunikacyjnych, które wykorzystują systemy transmisji widma rozproszonego z sekwencją bezpośrednią i systemy transmisji widma rozproszonego z przeskokiem częstotliwości , projekt wielowarstwowego odbłyśnika z dielektrykiem optycznym oraz w wydajnym projektowaniu niektórych eksperymentów fMRI .

Pokolenie

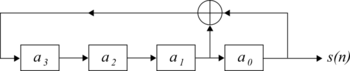
₀ Rysunek 1: Następna wartość rejestru a ₃ w rejestrze przesuwnym ze sprzężeniem zwrotnym o długości 4 jest określona przez sumę modulo-2 a i a ₁ .

MLS są generowane przy użyciu rejestrów przesuwnych z maksymalnym liniowym sprzężeniem zwrotnym . System generujący MLS z rejestrem przesuwnym o długości 4 pokazano na rys. 1. Można go wyrazić za pomocą następującej relacji rekurencyjnej:

{\ Displaystyle {\ rozpocząć {przypadki} a_ {3} [n + 1] = a_ {0} [n] + a_ {1} [n] \\ a_ {2} [n + 1] = a_{3}[n]\\a_{1}[n+1]=a_{2}[n]\\a_{0}[n+1]=a_{1}[n]\\\koniec{ sprawy}}}

gdzie n $2$ indeksem czasu i reprezentuje dodatek modulo- . Dla wartości bitowych 0 = FAŁSZ lub 1 = PRAWDA jest to równoznaczne z operacją XOR.

Ponieważ MLS są okresowe, a rejestry przesuwne przechodzą przez każdą możliwą wartość binarną (z wyjątkiem wektora zerowego), rejestry mogą być inicjowane do dowolnego stanu, z wyjątkiem wektora zerowego.

Interpretacja wielomianowa

Wielomian nad GF(2) może być powiązany z rejestrem przesuwnym z liniowym sprzężeniem zwrotnym . Ma stopień długości rejestru przesuwnego i ma współczynniki, które wynoszą 0 lub 1, odpowiadające zaczepom rejestru, które zasilają bramkę xor . Na przykład wielomian odpowiadający rysunkowi 1 to x ⁴ + x ³ + 1.

Warunkiem koniecznym i wystarczającym, aby sekwencja generowana przez LFSR miała maksymalną długość, jest to, aby odpowiadający jej wielomian był pierwotny .

Realizacja

MLS są niedrogie do wdrożenia w sprzęcie lub oprogramowaniu, a rejestry przesuwne ze sprzężeniem zwrotnym stosunkowo niskiego rzędu mogą generować długie sekwencje; sekwencja wygenerowana przy użyciu rejestru przesuwnego o długości 20 ma długość 2 ²⁰ − 1 próbek (1 048 575 próbek).

Własności ciągów o maksymalnej długości

MLS mają następujące właściwości, sformułowane przez Solomona Golomba .

Właściwość równowagi

Występowanie 0 i 1 w sekwencji powinno być w przybliżeniu takie samo. Dokładniej, w sekwencji o maksymalnej długości o długości ${\ Displaystyle 2 ^ {n} -1}$ jest ${\ Displaystyle 2 ^ {n-1}}$ jedynek i ${\ Displaystyle 2 ^ {n-1} -1}$ zera. Liczba jedynek jest równa liczbie zer plus jeden, ponieważ stan zawierający tylko zera nie może wystąpić.

Uruchom nieruchomość

„Run” to podsekwencja kolejnych „1” lub kolejnych „0” w danym MLS. Liczba przebiegów to liczba takich podsekwencji. ^{[ niejasne ]}

Spośród wszystkich „przebiegów” (składających się z „1” lub „0”) w sekwencji:

Połowa odcinków ma długość 1.
Jedna czwarta tras ma długość 2.
Jedna ósma tras ma długość 3.
... itd. ...

Właściwość korelacji

Okrągła autokorelacja MLS to funkcja delta Kroneckera (z przesunięciem DC i opóźnieniem czasowym, w zależności od implementacji). Dla konwencji ± 1, tj. Przypisuje się wartość bitu 1 i wartość bitu 0 ${\ Displaystyle$ $= -1}$ , odwzorowując XOR na ujemne iloczynu s = + :

${\ Displaystyle R (n) = {\ Frac {1} {N}} \ suma _ {m = 1} ^ {N} s [m] \, s ^ {*} [m + n] _ {N} ={\begin{przypadki}1&{\text{if }}n=0,\\-{\frac {1}{N}}&{\text{if }}0<n<N.\end{przypadki }}}$

gdzie reprezentuje złożony koniugat i $[$ $n] _ {N}}$ reprezentuje przesunięcie kołowe .

Liniowa autokorelacja MLS jest zbliżona do delty Kroneckera.

Ekstrakcja odpowiedzi impulsowych

Jeśli odpowiedź impulsowa systemu niezmiennego w czasie liniowym (LTI) ma być mierzona za pomocą MLS, odpowiedź można wyodrębnić ze zmierzonego wyjścia systemu y [ n ], biorąc jego kołową korelację krzyżową z MLS. Dzieje się tak, ponieważ autokorelacja MLS wynosi 1 dla zerowego opóźnienia i prawie zero (-1/ N , gdzie N to długość sekwencji) dla wszystkich innych opóźnień; innymi słowy, można powiedzieć, że autokorelacja MLS zbliża się do funkcji impulsu jednostkowego wraz ze wzrostem długości MLS.

Jeśli odpowiedź impulsowa systemu wynosi h [ n ], a MLS to s [ n ], to wtedy

{\ Displaystyle y [n] = (h * s) [n]. \,}

Biorąc korelację krzyżową względem s [ n ] obu stron,

{\ Displaystyle {\ phi} _ {sy} = h [n] * {\ phi} _ {ss} \,}

i zakładając, że φ _ss jest impulsem (dotyczy długich ciągów)

{\ displaystyle h [n] = {\ phi} _ {sy}. \,}

Do tego celu można wykorzystać dowolny sygnał z impulsową autokorelacją, ale sygnały o wysokim współczynniku szczytu , takie jak sam impuls, wytwarzają odpowiedzi impulsowe o słabym stosunku sygnału do szumu . Powszechnie przyjmuje się, że MLS byłby wówczas sygnałem idealnym, gdyż składa się tylko z wartości pełnej skali, a jego cyfrowy współczynnik szczytu to minimum 0 dB. Jednak po rekonstrukcji analogowej , ostre nieciągłości w sygnale tworzą silne piki między próbkami, obniżając współczynnik szczytu o 4-8 dB lub więcej, zwiększając się wraz z długością sygnału, czyniąc go gorszym niż przemiatanie sinusoidalne. Inne sygnały zostały zaprojektowane z minimalnym współczynnikiem szczytu, chociaż nie wiadomo, czy można go poprawić powyżej 3 dB.

Związek z transformacją Hadamarda

Cohn i Lempel wykazali związek MLS z transformatą Hadamarda . Ta zależność umożliwia korelacji MLS w szybkim algorytmie podobnym do FFT .

Zobacz też

Golomb, Solomon W.; Guang Gong (2005). Projekt sygnału dla dobrej korelacji: do komunikacji bezprzewodowej, kryptografii i radaru . Wydawnictwo Uniwersytetu Cambridge . ISBN 978-0-521-82104-9 .

Linki zewnętrzne

Bristow-Johnson, Robert. „Mały samouczek MLS” . — Krótki samouczek on-line opisujący, w jaki sposób MLS jest używany do uzyskiwania odpowiedzi impulsowej liniowego systemu niezmiennego w czasie . Opisuje również, w jaki sposób nieliniowości w systemie mogą objawiać się jako fałszywe skoki w pozornej odpowiedzi impulsowej.
Hej, Jens. „Pomiar odpowiedzi impulsowej za pomocą MLS” (PDF) . — Artykuł opisujący generację MLS. Zawiera kod C do generowania MLS przy użyciu do 18-tap-LFSR i pasującą transformatę Hadamarda do ekstrakcji odpowiedzi impulsowej.
Schäfer, Magnus (październik 2012). „Baza danych odpowiedzi impulsowych w Akwizgranie” . Instytut Systemów Komunikacyjnych i Przetwarzania Danych, Uniwersytet RWTH w Akwizgranie. wersja 1.4. Baza danych (obuusznych) odpowiedzi impulsowych pomieszczenia generowana za pomocą sekwencji o maksymalnej długości.
„Wydajne rejestry przesuwne, liczniki LFSR i generatory długich pseudolosowych sekwencji - przestarzałe” (PDF) . Xilinx. Lipiec 1996. XAPP052 v1.1. — Implementacja lfsr w układach FPGA obejmuje listę zaczepów dla 3 do 168 bitów