Skręt Dehna

Dodatni skręt Dehna zastosowany do cylindra wokół czerwonej krzywej c modyfikuje zieloną krzywą, jak pokazano.

W topologii geometrycznej , gałęzi matematyki , skręt Dehna jest pewnym rodzajem samohomeomorfizmu powierzchni ( rozmaitość dwuwymiarowa ).

Definicja

Skręt generała Dehna na zwartej powierzchni reprezentowanej przez n -gon.

Załóżmy, że c jest prostą zamkniętą krzywą na zamkniętej, orientowalnej powierzchni S . Niech A będzie cylindrycznym sąsiedztwem c . Wtedy A jest pierścieniem homeomorficznym z iloczynem kartezjańskim koła i przedziału jednostkowego I :

${\ Displaystyle c \ podzbiór A \ cong S ^ {1} \ razy I.}$

Podaj współrzędne A ( s , t ), gdzie s jest liczbą zespoloną postaci $\ Displaystyle e ^ {i \ theta}}$ z ${\ Displaystyle \ theta \ w [0, 2\pi ],}$ i t ∈ [0, 1] .

Niech f będzie mapą od S do samej siebie, która jest tożsamością na zewnątrz A i wewnątrz A , którą mamy

${\ Displaystyle f (s, t) = \ lewo (se ^ {i2 \ pi t}, t \ prawo).}$

Wówczas f jest skrętem Dehna wokół krzywej c .

Skręty Dehna można również zdefiniować na nieorientowalnej powierzchni S , pod warunkiem, że zaczyna się od dwustronnej prostej zamkniętej krzywej c na S .

Przykład

Przykład skrętu Dehna na torusie, wzdłuż zamkniętej krzywej a , na niebiesko, gdzie a jest krawędzią podstawowego wielokąta reprezentującego torus.

Automorfizm na grupie podstawowej torusa wywołany samohomeomorfizmem skrętu Dehna wzdłuż jednego z generatorów torusa.

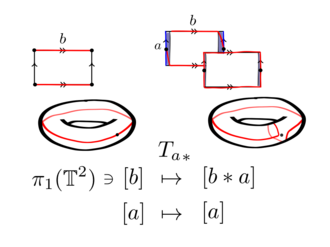
Rozważmy torus reprezentowany przez podstawowy wielokąt o krawędziach a i b

${\ Displaystyle \ mathbb {T} ^ {2} \ cong \ mathbb {R} ^ {2} / \ mathbb {Z} ^ {2}.}$

Niech zamknięta krzywa będzie linią biegnącą wzdłuż krawędzi za . ${\ displaystyle \ gamma _ {a}}$ .

$pod$ uwagę wybór sklejenia homeomorfizmu na figurze, cylindryczne sąsiedztwo krzywej jak pasmo połączone wokół pączka. Powiedzmy, że to sąsiedztwo jest homeomorficzne dla pierścienia

${\ Displaystyle a (0; 0,1) = \ {z \ w \ mathbb {C}: 0 <| z | <1 \}}$

w płaszczyźnie złożonej.

Rozszerzając do torusa mapę skręcania ${\ Displaystyle \ lewo (e ^ {i \ theta}, t \ prawo) \ mapsto \ lewo (e ^ {i \ lewo (\ theta + 2 \ pi t \ prawo)}, t \ prawo)}$ pierścienia, przez homeomorfizmy pierścienia do otwartego cylindra do sąsiedztwa ${\ Displaystyle \ gamma _{a}}$ , daje skręt Dehna torusa o a .

${\ Displaystyle T_ {a}: \ mathbb {T} ^ {2} \ do \ mathbb {T} ^ {2}}$

Ten własny homeomorfizm działa na zamkniętą krzywą wzdłuż b . W sąsiedztwie rurowym przyjmuje krzywą b raz wzdłuż krzywej a .

Homeomorfizm między przestrzeniami topologicznymi indukuje naturalny izomorfizm między ich podstawowymi grupami . Dlatego jeden ma automorfizm

${\ Displaystyle {T_ {a}} _ {\ ast}: \ pi _ {1} \left(\mathbb {T} ^{2}\right)\to \pi _{1}\left(\mathbb {T} ^{2}\right):[x]\mapsto \left[T_{a }(x)\prawo]}$

gdzie [ x ] to klasy homotopii zamkniętej krzywej x w torusie. Uwaga $\ Displaystyle {T_ {a}} _ {\ ast} ([a]) = [a]}$ i $\ Displaystyle {T_ {a}} _ {\ ast} ([b]) = [b * a]}$ , gdzie ${\ Displaystyle b * a}$ to ścieżka przebyta wokół b , a następnie za .

Mapowanie grupy klas

3 g - 1 z twierdzenia o skręcie, pokazane tutaj dla g = 3.

Twierdzenie Maxa Dehna mówi, że $powierzchni$ tej postaci generują grupę klas mapowania klas izotopów zachowujących orientację homeomorfizmów dowolnego zamkniętego, zorientowanego rodzaju . WBR Lickorish później ponownie odkrył ten $odwzorowania ($ za pomocą prostszego dowodu, a ponadto wykazał, że skręcanie Dehna wzdłuż się to żartobliwą nazwą „twierdzenie o skręcie Lickorish” ; liczba ta została później poprawiona przez Stephena P. Humphriesa do ${\ displaystyle 2g + 1}$ , dla ${\ displaystyle g> 1}$ , co, jak pokazał, było liczbą minimalną.

Lickorish uzyskał również analogiczny wynik dla powierzchni nieorientowalnych, które wymagają nie tylko skrętów Dehna, ale także „ Y-homeomorfizmów ”.

Zobacz też

• Latarniowa relacja

•   Andrew J. Casson , Steven A Bleiler, Automorfizmy powierzchni po Nielsenie i Thurstonie , Cambridge University Press , 1988. ISBN 0-521-34985-0 .
• Stephen P. Humphries, „Generatory dla grupy klas mapowania”, w: Topologia rozmaitości niskowymiarowych ( Proc. Second Sussex Conf. , Chelwood Gate, 1977), s. 44–47, Lecture Notes in Math., 722, Springer , Berlin, 1979. MR 0547453
• WBR Lickorish , „Reprezentacja orientowalnych kombinatorycznych 3-rozmaitości”. Ann. z matematyki. (2) 76 1962 531-540. MR 0151948
• WBR Lickorish, „Skończony zbiór generatorów dla grupy homotopii 2-rozmaitości”, Proc. Cambridge Philos. soc. 60 (1964), 769–778. MR 0171269