Podstawowy wielokąt

W matematyce podstawowy wielokąt można zdefiniować dla każdej zwartej powierzchni Riemanna rodzaju większej niż 0. Koduje on nie tylko topologię powierzchni poprzez jej grupę podstawową , ale także określa powierzchnię Riemanna aż do konforemnej równoważności. Zgodnie z twierdzeniem o uniformizacji każda zwarta powierzchnia Riemanna ma po prostu połączoną uniwersalną powierzchnię pokrywającą określoną przez dokładnie jedną z poniższych zależności:

sfera Riemanna ,
płaszczyzna złożona ,
dysk jednostkowy D lub równoważnie górna półpłaszczyzna H .

W pierwszym przypadku rodzaju zero powierzchnia jest konforemnie równoważna kuli Riemanna.

W drugim przypadku rodzaju pierwszego powierzchnia jest konforemnie równoważna torusowi C /Λ dla pewnej sieci Λ w C . Podstawowy wielokąt Λ, jeśli przyjmie się, że jest wypukły, można uznać za równoległobok okresowy lub sześciokąt centralnie symetryczny, co po raz pierwszy udowodnił Fiodorow w 1891 roku.

W ostatnim przypadku rodzaju g > 1 powierzchnia Riemanna jest konforemnie równoważna H /Γ, gdzie Γ jest fuchsowską grupą przekształceń Möbiusa . Podstawowa dziedzina dla Γ jest określona przez wielokąt wypukły dla metryki hiperbolicznej na H . Można je zdefiniować za pomocą wielokątów Dirichleta i mieć parzystą liczbę boków. Z takiego wielokąta można odczytać strukturę grupy podstawowej Γ. Korzystając z teorii odwzorowań quasikonformalnych i równania Beltramiego , można pokazać, że istnieje kanoniczny wypukły wielokąt Dirichleta o bokach 4 g , po raz pierwszy zdefiniowany przez Fricke'a , który odpowiada standardowej prezentacji Γ jako grupy z 2 g generatorami a ₁ , b ₁ , za ₂ , b ₂ , ..., za _g , b _g i pojedyncza relacja [ za ₁ , b ₁ ][ za ₂ , b ₂ ] ⋅⋅⋅ [ a _g , b _g ] = 1, gdzie [ za , b ] = za b za ^-1 b ^-1 .

Każda metryka Riemanna na zorientowanej zamkniętej 2-rozmaitości M definiuje złożoną strukturę na M , czyniąc M zwartą powierzchnią Riemanna. Dzięki zastosowaniu fundamentalnych wielokątów wynika, że dwie zorientowane zamknięte 2-rozmaitości są klasyfikowane według ich rodzaju, czyli połowy rzędu grupy abelowej Γ/[Γ,Γ], gdzie Γ = π $1$ ₍ M ) . Ponadto z teorii odwzorowań quasikonformalnych wynika również, że dwie zwarte powierzchnie Riemanna są dyfeomorficzne wtedy i tylko wtedy, gdy są homeomorficzne. W konsekwencji dwie zamknięte zorientowane 2-rozmaitości są homeomorficzne wtedy i tylko wtedy, gdy są dyfeomorficzne. Taki wynik można również udowodnić za pomocą metod topologii różniczkowej .

Podstawowe wielokąty w rodzaju pierwszym

Równoległoboki i centralnie symetryczne sześciokąty

jest podstawowy wielokąt wypukły dla działania przez translację Λ = Z a ⊕ Z b na R ² = C , gdzie aib są liniowo niezależne od R . (Po przeprowadzeniu rzeczywistej transformacji liniowej na R ² , można w razie potrzeby założyć, że Λ = Z ² = Z + Z i ; dla jednego rodzaju powierzchni Riemanna można przyjąć postać Λ = Z ² = Z + Z ω, gdzie Im ω > 0.) Dziedzina fundamentalna jest dana równoległobokiem $s x + t y$ dla $0 < s, t < 1$ , gdzie $x$ i $y$ są generatorami Λ.

Jeśli C jest wnętrzem podstawowego wielokąta wypukłego, to translacja C + x obejmuje R ² , gdy x przebiega przez Λ. Wynika z tego, że punkty brzegowe C są utworzone z przecięć C ∩ ( C + x ). Są to zwarte zbiory wypukłe w ∂ C , a zatem albo wierzchołki C , albo boki C. Wynika z tego, że każdą zamkniętą stronę C można zapisać w ten sposób. Przekładając przez − x wynika, że C ∩ ( C − x ) jest również bokiem C . Zatem boki C występują w równoległych parach o równej długości. Punkty końcowe dwóch takich równoległych odcinków o równej długości można połączyć tak, że się przecinają, a przecięcie następuje w punktach środkowych odcinków linii łączących punkty końcowe. Wynika z tego, że przecięcia wszystkich takich odcinków występują w tym samym punkcie. Przekładając ten punkt na początek, wynika z tego, że wielokąt jest centralnie symetryczny; to znaczy, jeśli punkt z znajduje się w wielokącie, to także - z .

Łatwo zauważyć translacje centralnie symetrycznego wypukłego tesselatu sześciokąta na płaszczyźnie. Jeśli A jest punktem sześciokąta, to sieć jest generowana przez wektory przemieszczenia AB i AC , gdzie B i C to dwa wierzchołki, które nie są sąsiadami A i nie są naprzeciw A . Rzeczywiście, drugi rysunek pokazuje, w jaki sposób sześciokąt jest równoważny równoległobokowi otrzymanemu przez przesunięcie dwóch trójkątów odciętych przez odcinki AB i AC . Równie dobrze pierwsze zdjęcie pokazuje inny sposób łączenia płytek za pomocą równoległoboków z sześciokątnymi płytkami. Jeśli środek sześciokąta to 0, a wierzchołki w kolejności to a , b , c , - a , - b i - c , to Λ jest grupą abelową z generatorami $a + b$ i $b + c$ .

Przykłady podstawowych wielokątów generowanych przez równoległoboki

Istnieją dokładnie cztery topologie, które można utworzyć, identyfikując boki rombu na różne sposoby. Są one podane poniżej jako krawędzie kierunkowe A i B na kwadracie, jako sekwencje AABB lub ABAB.

Nazwa	Kula	Torus	Płaszczyzna rzutowa	Butelka Kleina
Orientowalny	Tak		NIE
Całkowita krzywizna	4π	0	2π	0
Topologia ABAB (kwadrat)		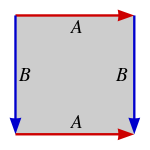${\ Displaystyle ABA ^ {- 1} B ^ {- 1}}$	${\ Displaystyle ABAB}$	${\ Displaystyle ABAB ^ {- 1}}$ (lub ${\ Displaystyle ABA ^ {- 1} B}$ )
Topologia AABB (kwadrat)	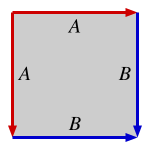${\ Displaystyle ABB ^ {- 1} A ^ {- 1}}$		${\ Displaystyle ABB ^ {- 1} A}$ (lub ${\ Displaystyle ABBA ^ {- 1}}$ )	${\ Displaystyle ABBA}$
Geometria	Kula	Torus	Półkula	Pół torusa

Twierdzenie Fiodorowa

Twierdzenie Fiodorowa , ustanowione przez rosyjskiego krystalografa Jewgrafa Fiodorowa w 1891 r., stwierdza, że równoległoboki i centralnie symetryczne sześciokąty są jedynymi wypukłymi wielokątami, które są podstawowymi domenami. Istnieje na to kilka dowodów, niektóre z nowszych odnoszą się do wyników teorii wypukłości , geometrii liczb i pakowania kół , takich jak nierówność Brunna-Minkowskiego . Przedstawione zostaną tutaj dwa elementarne dowody pochodzące od HSM Coxetera i Voronoi .

Dowód Coxetera przebiega przy założeniu, że istnieje centralnie symetryczny wypukły wielokąt C o bokach 2 m . Następnie duży zamknięty równoległobok utworzony z N ² podstawowych równoległoboków jest złożony z translacji C , które wychodzą poza krawędzie dużego równoległoboku. To indukuje kafelkowanie na torusie C / N Λ. Niech v , e i f będą liczbą wierzchołków, krawędzi i ścian w tym kafelku (biorąc pod uwagę identyfikacje w przestrzeni ilorazowej). Następnie, ponieważ charakterystyka Eulera-Poincarégo torusa wynosi zero,

{\ Displaystyle ve + f = 0.}

Z drugiej strony, ponieważ każdy wierzchołek znajduje się na co najmniej 3 różnych krawędziach i każda krawędź znajduje się między dwoma wierzchołkami,

{\ displaystyle 3v \ równoważnik 2e.}

Ponadto, ponieważ każda krawędź leży na dokładnie dwóch ścianach,

{\ displaystyle 2e = 2mf.}

Stąd

{\ Displaystyle mf = e \ równoważnik 3 (ev) = 3f.}

aby

{\ Displaystyle m \ równoważnik 3,}

jako wymagane.

Dowód Woronoja zaczyna się od obserwacji, że każda krawędź C odpowiada elementowi x z Λ. W rzeczywistości krawędź jest dwusieczną prostopadłą promienia od 0 do x . Stąd stopa prostopadłej od 0 do każdej krawędzi leży we wnętrzu każdej krawędzi. Jeśli y jest dowolnym punktem sieci, to 1/2 y nie może leżeć w C ; bo jeśli tak, to –1/2 y również leżałoby w C , zaprzeczając, że C jest dziedziną podstawową dla Λ. Niech ± x ₁ , ..., ± x _m będą 2 m różnymi punktami Λ odpowiadającymi bokom C . Napraw generatory a i b z Λ. Zatem x _i = α _i a + β _i b , gdzie α _i oraz β _i są liczbami całkowitymi. Nie jest możliwe, aby zarówno α _i, jak i β _i były parzyste, ponieważ w przeciwnym razie ± 1/2 x _i byłoby punktem Λ na boku, co jest sprzeczne z tym, że C jest dziedziną podstawową. Istnieją więc trzy możliwości dla pary liczb całkowitych (α _i , β _i ) modulo 2: (0,1), (1,0) i (1,1). W konsekwencji, jeśli m > 3, istniałyby x _i i x _j z i ≠ j z obiema współrzędnymi x _i − x _j parzystymi, tj. 1/2 ( x _i + x _j ) leży w Λ. Ale to jest środek odcinka linii łączącego dwa wewnętrzne punkty krawędzi, a zatem leży w C , wnętrzu wielokąta. To znowu zaprzecza faktowi, że C jest domeną podstawową. Więc reductio ad absurdum m ≤ 3, jak twierdzono.

Domeny Dirichlet-Voronoi

Dla sieci Λ w C = R2 podstawową domenę można zdefiniować kanonicznie za pomocą konforemnej ^struktury C . Zauważ, że grupa przekształceń konforemnych C jest dana przez złożone przekształcenia afiniczne g ( z ) = az + b z a ≠ 0 . Te przekształcenia zachowują metrykę euklidesową d ( z , w ) = | z - w | do współczynnika, jak również zachowując orientację . Jest to podgrupa grupy Möbiusa ustalająca punkt w ∞. Struktury metrycznej można użyć do zdefiniowania kanonicznej domeny podstawowej przez C = { z : d ( z , 0) < d ( z , λ ) dla wszystkich λ ≠ 0 w Λ}. (Z definicji wynika, że jest to dziedzina podstawowa.) To jest przykład domeny Dirichleta lub diagramu Woronoja : ponieważ złożone translacje tworzą grupę abelową, więc dojeżdżają z działaniem Λ, te koncepcje są zbieżne. Kanoniczna dziedzina podstawowa dla Λ = Z + Z ω z Im ω > 0 jest albo symetrycznym równoległobokiem wypukłym, albo sześciokątem o środku 0. Przez równoważność konforemną okres ω można dodatkowo ograniczyć, aby spełnić | Re ω | ≤ 1/2 i | ω | ≥ 1 . Jak Dirichlet („Twierdzenie Dirichleta o sześciokącie”, 1850), dla prawie wszystkich ω dziedziną podstawową jest sześciokąt. Dla Re ω > 0 , środki boków są określone przez ±1/2, ± ω /2 i ±( ω – 1)/2 ; boki przecinają odpowiednie promienie prostopadle od 0, co całkowicie określa wierzchołki. W rzeczywistości pierwszy wierzchołek musi mieć postać (1 + ix )/2 i ω (1 + iy )/2 z x i y rzeczywistymi; więc jeśli ω = a + ib , to a – przez = 1 i x = b + ay . Stąd y = ( za – 1)/ b i x = ( za ² + b ² – za )/ b . Sześć wierzchołków to zatem ± ω (1 – iy )/2 i ± (1 ± ix )/2 .

Podstawowe wielokąty w wyższym rodzaju

Przegląd

Każda zwarta powierzchnia Riemanna X ma uniwersalną powierzchnię pokrywającą , która jest prosto spójną powierzchnią Riemanna X . Podstawowa grupa X działa jako przekształcenia pokładowe X i może być utożsamiana z podgrupą Γ grupy biholomorfizmów X . Grupa Γ działa więc swobodnie na X ze zwartą przestrzenią ilorazową X /Γ, którą można utożsamiać z X . Zatem klasyfikację zwartych powierzchni Riemanna można sprowadzić do badania możliwych grup Γ. Zgodnie z twierdzeniem o uniformizacji X jest albo sferą Riemanna, płaszczyzną zespoloną, albo jednostkowym dyskiem/górną półpłaszczyzną. Pierwszym ważnym niezmiennikiem zwartej powierzchni Riemanna jest jej rodzaj , niezmiennik topologiczny określony przez połowę rzędu grupy abelowej Γ/[Γ, Γ] (którą można utożsamiać z grupą homologii H ₁ ( X , Z ) ). Rodzaj wynosi zero, jeśli przestrzenią pokrywającą jest sfera Riemanna; jeden, jeśli jest to płaszczyzna zespolona; i większa niż jeden, jeśli jest to dysk jednostkowy lub górna półpłaszczyzna.

Bihomolomorfizmy sfery Riemanna to po prostu złożone transformacje Möbiusa, a każda transformacja nietożsamościowa ma co najmniej jeden punkt stały, ponieważ odpowiednia macierz zespolona ma zawsze co najmniej jeden niezerowy wektor własny. Zatem jeśli X jest sferą Riemanna, to X musi być po prostu połączony i biholomorficzny ze sferą Riemanna, rodzajem zerowej powierzchni Riemanna. Gdy X jest płaszczyzną zespoloną, grupa biholomorfizmów jest grupą afiniczną, zespolonymi transformacjami Möbiusa ustalającymi ∞, więc transformacje g ( z ) = az + b z a ≠ 0 . Transformacje nietożsamościowe bez punktów stałych to tylko te, w których a = 1 i b ≠ 0 , tj. translacje niezerowe. Grupę Γ można zatem utożsamić z siecią Λ w C i X z ilorazem C / Λ, jak opisano w części dotyczącej podstawowych wielokątów w rodzaju pierwszym. W trzecim przypadku, gdy X jest tarczą jednostkową lub górną półpłaszczyzną, grupa biholomorfizmów składa się ze złożonych przekształceń Möbiusa ustalających okrąg jednostkowy lub oś rzeczywistą. W pierwszym przypadku przekształcenia odpowiadają elementom grupy SU(1, 1)/{± I }; w tym drugim przypadku odpowiadają one rzeczywistym transformacjom Möbiusa, a więc elementom SL(2, R )/{± I }.

Badanie i klasyfikacja możliwych grup Γ, które działają swobodnie na dysku jednostkowym lub górnej półpłaszczyźnie ze zwartym ilorazem - grup Fuchsa pierwszego rodzaju - można przeprowadzić, badając ich podstawowe wielokąty, jak opisano poniżej. Jak Poincaré , każdy taki wielokąt ma szczególne właściwości, a mianowicie jest wypukły i ma naturalną parę między bokami. Pozwalają one nie tylko na odzyskanie grupy, ale zapewniają wyraźną prezentację grupy przez generatory i relacje. I odwrotnie, Poincaré udowodnił, że każdy taki wielokąt daje zwartą powierzchnię Riemanna; w rzeczywistości twierdzenie Poincarégo o wielokątach miało zastosowanie do bardziej ogólnych wielokątów, gdzie wielokąt mógł mieć idealne wierzchołki, ale jego dowód był kompletny tylko w przypadku zwartym, bez takich wierzchołków. Bez założeń dotyczących wypukłości wielokąta, kompletne dowody zostały podane przez Maskit i de Rham , w oparciu o ideę Siegela , i można je znaleźć w Beardon (1983) , Iversen (1992) i Stillwell (1992) . Carathéodory omówił elementarnie istnienie teselacji trójkątami Schwarza , tj. nachylenia trójkątów geodezyjnych o kątach $π$ / a , $π$ / b , $π$ / c o sumie mniejszej niż $π ,$ gdzie a , b , c są liczbami całkowitymi. Gdy wszystkie kąty są równe $π$ /2 g , ustanawia to kafelkowanie za pomocą regularnych wielokątów hiperbolicznych o boku 4g , a zatem istnienie określonej zwartej powierzchni Riemanna rodzaju g jako przestrzeni ilorazowej. Ten szczególny przykład, który ma grupę cykliczną Z2g o symetrii bihomolomorficznej, _{jest używany} w poniższym rozwinięciu.

Klasyfikacja do homeomorfizmu i dyfeomorfizmu zwartych powierzchni Riemanna implikuje klasyfikację zamkniętych orientowalnych 2-rozmaitości do homeomorfizmu i dyfeomorfizmu: dowolne dwie 2-rozmaitości tego samego rodzaju są dyfeomorficzne. W rzeczywistości, używając podziału jedności, każda zamknięta 2-rozmaitość orientowalna dopuszcza metrykę riemannowską . Dla zwartej powierzchni Riemanna można również wprowadzić metrykę konforemną, która jest konforemna, tak że we współrzędnych holomorficznych metryka przyjmuje postać ρ ( z ) | dz | ² . Po wybraniu tej metryki, lokalnie odwzorowania biholomorficzne są dokładnie zachowującymi orientację dyfeomorfizmami, które są konforemne, tj. skalują metrykę za pomocą funkcji gładkiej. Istnienie współrzędnych izotermicznych — co można udowodnić za pomocą lokalnych twierdzeń o istnieniu dla równania Laplaciana lub Beltramiego — pokazuje, że każdej zamkniętej zorientowanej rozmaitości riemannowskiej 2 można nadać złożoną strukturę zgodną z jej metryką, a zatem ma strukturę a zwarta powierzchnia Riemanna. Ta konstrukcja pokazuje, że klasyfikację zamkniętych orientowalnych 2-rozmaitości aż do dyfeomorfizmu lub homeomorfizmu można sprowadzić do przypadku zwartych powierzchni Riemanna.

Klasyfikację aż do homeomorfizmu i dyfeomorfizmu zwartych powierzchni Riemanna można przeprowadzić za pomocą wielokąta podstawowego. Rzeczywiście, jak zauważył Poincaré, wypukłe podstawowe wielokąty dla zwartych powierzchni Riemanna H / Γ można skonstruować, adaptując metodę Dirichleta z przestrzeni euklidesowej do przestrzeni hiperbolicznej. Następnie, podążając za Nevanlinną i Jostem, domenę podstawową można stopniowo modyfikować, aby uzyskać niewypukły wielokąt z wierzchołkami leżącymi na pojedynczej orbicie Γ i fragmentarycznymi bokami geodezyjnymi. Relacja parowania po bokach jest również modyfikowana w każdym z tych kroków. Każdy krok obejmuje przecięcie wielokąta przez ukośny segment geodezyjny we wnętrzu wielokąta i ponowne złożenie wielokąta przy użyciu jednej z transformacji Möbiusa zaangażowanych w parowanie. Żadne dwa sparowane boki nie mogą mieć wspólnego wierzchołka w ostatecznej relacji parowania, która spełnia podobne właściwości do pierwotnej relacji. Ten wielokąt można z kolei sukcesywnie modyfikować, składając wielokąt po przecięciu go ukośnym segmentem geodezyjnym w jego wnętrzu. Końcowy wielokąt ma wierzchołki równoważne 4 g , z bokami, które są fragmentarycznie geodezyjne. Boki są oznaczone elementami grupowymi, które dają transformację Möbiusa na sparowaną stronę. W kolejności etykietowania jest

a_ {1}, b_ {1}, a_ {1 }^{-1},b_{1}^{-1},\kropki ,a_{g},b_{g},a_{g}^{-1},b_{g}^{-1}, }

tak, że Γ jest generowane przez a i _oraz b i _podlegające pojedynczej relacji

{\ Displaystyle a_ {1} b_ {1} a_ {1} ^ {- 1} b_ { 1}^{-1}\cdots a_{g}b_{g}a_{g}^{-1}b_{g}^{-1}=1.}

Powierzchnia zerowa rodzaju (kula)
Rodzaj jedna powierzchnia ( torus )
Powierzchnia rodzaju dwa
Powierzchnia rodzaju trzeciego

Korzystając z teorii liczb przecięć , wynika, że kształt uzyskany przez połączenie wierzchołków za pomocą geodezji jest również wielokątem właściwym, niekoniecznie wypukłym, a także jest dziedziną podstawową z tymi samymi elementami grupowymi dającymi parowanie. Daje to podstawowy wielokąt z krawędziami określonymi przez segmenty geodezyjne i ze standardowym etykietowaniem. Abelianizacja Γ, grupa ilorazowa Γ/[Γ, Γ] , jest wolną grupą abelową z generatorami 2 g . Zatem rodzaj g jest niezmiennikiem topologicznym. Łatwo zauważyć, że dwie powierzchnie Riemanna tego samego rodzaju są homeomorficzne, ponieważ jako przestrzeń topologiczna są uzyskiwane przez identyfikację boków wielokąta o boku 4 g — wielokąta euklidesowego w modelu Kleina — przez dyfeomorfizmy między sparowanymi bokami. Zastosowanie tej konstrukcji do regularnego wielokąta o bokach 4 g pozwala na topologiczne spojrzenie na powierzchnię Riemanna jako pączek z otworami g , co jest standardowym opisem zorientowanych powierzchni w tekstach wprowadzających do topologii.

Istnieje kilka dalszych wyników:

Dwie homeomorficzne powierzchnie Riemanna są dyfeomorficzne.
Każdy wypukły podstawowy wielokąt w rodzaju g ma N wierzchołków, gdzie 4 g ≤ N ≤ 12 g – 6.
Wielokąt Dirichleta w rodzaju g ma dokładnie 12 g – 6 wierzchołków dla gęstego otwartego zbioru centrów.
Każda powierzchnia Riemanna rodzaju g ma podstawowy wielokąt Fricke'a, tj. wielokąt wypukły z kanonicznymi parami między bokami. (Wielokąt niekoniecznie musi być wielokątem Dirichleta).
Po odpowiedniej normalizacji i oznaczeniu generatorów grupy podstawowej wielokąt Frickego jest jednoznacznie wyznaczony, a opisujące go parametry rzeczywiste 6 g – 6 mogą być użyte jako globalne rzeczywiste parametry analityczne dla przestrzeni Teichmüllera w rodzaju g .

Wyniki te są powiązane z wzajemnymi relacjami między homeomorfizmami a grupą podstawową: odzwierciedla to fakt, że grupa klas odwzorowania powierzchni Riemanna - grupa quasikonformalnych autohomomorfizmów powierzchni Riemanna H / Γ modulo tych homotopijnych do tożsamości - można utożsamiać z zewnętrzną grupą automorfizmów Γ ( twierdzenie Dehna – Nielsena – Baera ). Aby zobaczyć ten związek, zauważmy, że jeśli f jest quasi-konformalnym homeomorfizmem X ₁ = H /Γ ₁ na X ₂ = H /Γ ₂ , to f wznosi się do quasi-konformalnego homeomorfizmu f H na siebie. Ten wyciąg jest unikalny aż do pre-kompozycji z elementami Γ ₁ i post-kompozycji z elementami Γ ₂ . Jeśli $π$ _i jest rzutem H na X _i , to f ∘ $π$ ₁ = $π$ ₂ ∘ f i Γ _i jest po prostu grupą homeomorfizmów g z H takich, że $π$ _i ∘ g = $π$ _i . Jeśli wynika z tego, że f g = θ ( g ) f dla g w Γ ₁ , gdzie θ jest izomorfizmem grupowym Γ ₁ na Γ ₂ . Inny wybór zmian f θ według składu z wewnętrznym automorfizmem: mówi się, że takie izomorfizmy są równoważne .

Dwa izomorfizmy θ i θ ′ są równoważne wtedy i tylko wtedy, gdy odpowiadające im homeomorfizmy f i f ' są homotopijne. W rzeczywistości wystarczy pokazać, że quasikonformalny samohomeomorfizm f powierzchni indukuje wewnętrzny automorfizm grupy podstawowej wtedy i tylko wtedy, gdy jest homotopijny względem mapy tożsamości: innymi słowy homomorfizm quasikonformalnej grupy samohomeomorfizmów H /Γ do Out Γ przechodzi do grupy klas mapowania, w której jest wstrzykiwany. Rzeczywiście, załóżmy najpierw, że F ( t ) jest ciągłą ścieżką autohomeomorfizmów z F (0) = id i F (1) = f . Następnie występuje ciągła winda F ( t ) z F (0) = id. Co więcej, dla każdego g w Γ, F ( t ) ∘ g ∘ F ( t ) ⁻¹ jest ciągle zmieniającym się elementem Γ równym g dla t = 0 ; więc dyskretność Γ wymusza, aby ten element był stały, a zatem równy g , tak że F ( t ) komutuje z Γ, więc F (1) indukuje trywialny automorfizm. Jeśli natomiast F jest quasikonformalnym podniesieniem f indukującym wewnętrzny automorfizm Γ, to po złożeniu z elementem Γ w razie potrzeby można założyć, że F komutuje z Γ. Ponieważ F jest quasikonformalna, rozciąga się na quasi-symetryczny homeomorfizm koła, które również dojeżdża z Γ. Każdy g ≠ id w Γ jest hiperboliczny, więc ma dwa stałe punkty na okręgu a _± takie, że dla wszystkich innych punktów z g ^{± n} ( z ) dąży do a _± , tak jak n dąży do nieskończoności. Stąd F musi ustalić te punkty; ponieważ te punkty są gęste w okręgu, gdy g się zmienia, wynika z tego, że F ustala okrąg jednostkowy. Niech μ = F _z / F _z , aby μ było Γ-niezmienniczą różniczką Beltramiego. Niech F ( t ) będzie rozwiązaniem równania Beltramiego tμ znormalizowanego do ustalenia trzech punktów na okręgu jednostkowym. Wtedy F ( t ) komutuje z Γ i tak, jak dla F = F (1) , jest tożsamością na okręgu jednostkowym. Z konstrukcji F ( t ) jest izotopem między tożsamością a F . Dowodzi to iniekcji.

Dowód suriektywności polega na porównaniu metryki hiperbolicznej na D z metryką długości słowa na Γ. Zakładając bez utraty ogólności, że 0 leży we wnętrzu wypukłego wielokąta podstawowego C , a g jest elementem Γ, promień od 0 do g (0) - geodezyjny hiperboliczny - przechodzi przez szereg translacji C . Każdy z nich uzyskuje się z poprzedniego, stosując generator Γ lub stały iloczyn generatorów (jeśli kolejne translacje spotykają się w wierzchołku). Wynika z tego, że odległość hiperboliczna między 0 a g (0) jest mniejsza niż 4 g razy długość słowa g plus dwukrotna średnica podstawowego wielokąta. Zatem metryka na Γ re ₁ ( g , h ) = L ( h ⁻¹ g ) zdefiniowana przez długość słowa L ( g ) spełnia

{\ Displaystyle d (g (0), h (0)} \ równoważnik a \, d_ {1} (g, h) +b}

dla dodatnich stałych a i b . Odwrotnie, istnieją dodatnie stałe c i d takie, że

{\ Displaystyle d_ {1} (g, h) \ równoważnik c \, d (g (0), h (0)) + re.}

Wielokąty Dirichleta

Biorąc pod uwagę punkt $swobodnie$ górnej półpłaszczyźnie H i dyskretną podgrupę Γ PSL (2, R ) , która działa w sposób nieciągły na górnej półpłaszczyźnie, można zdefiniować wielokąt Dirichleta jako zbiór punktów

{\ Displaystyle F = \ {z \ in \ mathbf {H}: d (z, z_{0})<d(z,gz_{0})\;\;\forall g\in \Gamma ,g\neq 1\}}

Tutaj d jest metryką hiperboliczną na górnej półpłaszczyźnie. Podstawowy wielokąt metryczny jest częściej nazywany wielokątem Dirichleta .

Ten podstawowy wielokąt jest podstawową domeną .
Ten podstawowy wielokąt jest wypukły , ponieważ geodezyjne połączenie dowolnych dwóch punktów wielokąta jest całkowicie zawarte wewnątrz wielokąta.
Średnica F jest mniejsza lub równa średnicy H / Γ . W szczególności domknięcie F jest zwarte.
Jeśli Γ nie ma punktów stałych w H i H /Γ jest zwarty, to F będzie miało skończenie wiele boków.
Każdy bok wielokąta jest łukiem geodezyjnym .
Dla każdego boku s wielokąta istnieje dokładnie jeden inny bok s ′ taki, że gs = s ′ dla pewnego g w Γ. Zatem ten wielokąt będzie miał parzystą liczbę boków.
Zbiór elementów grupowych g , które łączą ze sobą boki, jest generatorami Γ i nie ma mniejszego zbioru, który wygeneruje Γ.
Górna półpłaszczyzna jest wyłożona płytkami przez zamknięcie F pod działaniem Γ. $\ overline {F}}}$ { gdzie ${\ Displaystyle {\ overline {F} }}$ jest zamknięciem F .

Znormalizowany wielokąt

W tej sekcji, zaczynając od dowolnego wielokąta Dirichleta, zostanie podany opis metody Nevanlinny (1953) , opracowanej przez Josta (2002) , modyfikacji wielokąta na wielokąt niewypukły z wierzchołkami równoważnymi 4 g i kanoniczną parowanie po bokach. To traktowanie jest analitycznym odpowiednikiem klasycznej topologicznej klasyfikacji orientowalnych dwuwymiarowych wielościanów, przedstawionej w Seifert & Threlfall (1934) .

Wielokąt kanoniczny Fricke'a

Biorąc pod uwagę powierzchnię Riemanna rodzaju g większą niż jeden, Fricke opisał inny podstawowy wielokąt, wielokąt kanoniczny Fricke'a , który jest bardzo szczególnym przykładem wielokąta Dirichleta. Wielokąt jest związany ze standardowym przedstawieniem podstawowej grupy powierzchni. Oryginalna konstrukcja Fricke'a jest skomplikowana i opisana w Fricke & Klein (1897) . Korzystając z teorii odwzorowań quasikonformalnych Ahlforsa i Bersa , Keen (1965) podał nową, krótszą i dokładniejszą wersję konstrukcji Fricke'a. Wielokąt kanoniczny Fricke ma następujące właściwości:

Wierzchołki wielokąta Fricke'a mają 4 wierzchołki g , z których wszystkie leżą na orbicie Γ. Przez wierzchołek rozumie się punkt, w którym spotykają się dwie strony.
Boki są dopasowane w różne pary, tak że istnieje unikalny element Γ przenoszący bok na sparowaną stronę, odwracając orientację. Ponieważ działanie Γ zachowuje orientację, jeśli jedna strona nazywa się $.$ $druga$ z pary może być oznaczona
Krawędzie standardowego wielokąta można ułożyć w taki sposób, aby lista sąsiednich boków miała postać ${\ Displaystyle A_ {1} B_ {1} A_ {1} ^ {-1} B_ {1} ^ {- 1} A_ {2} B_ {2} A_ {2} ^ {- 1}B_{2}^{-1}\cdots A_{g}B_{g}A_{g}^{-1}B_{g}^{-1}}$ . Oznacza to, że pary boków można ułożyć tak, że przeplatają się w ten sposób.
Boki są łukami geodezyjnymi.
Każdy z kątów wewnętrznych wielokąta Fricke'a jest dokładnie mniejszy niż $π$ , tak więc wielokąt jest ściśle wypukły, a suma tych kątów wewnętrznych wynosi 2 $π$ .

Powyższa konstrukcja jest wystarczająca do zagwarantowania, że każdy bok wielokąta jest zamkniętą (nietrywialną) pętlą na powierzchni Riemanna H /Γ. Jako taka, każda strona może zatem być elementem grupy podstawowej ${\ Displaystyle \ pi _ {1} (\ mathbb {H} / \ Gamma) \ równoważnik \ Gamma}$ . ${\ Displaystyle A_ {1}, B_ {1}, A_ {2}, B_ {2}, \ cdots A_ {g}, B_ {g}}$ grupa ma $B$ g ⋯ z dokładnie jednym ograniczeniem definiującym,

A_ {1} B_

.

Rodzajem powierzchni Riemanna H /Γ jest g .

Obszar

Pole standardowego wielokąta podstawowego wynosi ${\ Displaystyle 4 \ pi (g-1)}$ gdzie g jest rodzajem powierzchni Riemanna (równoważnie, gdzie 4 g to liczba boków wielokąt). Ponieważ standardowy wielokąt jest przedstawicielem H /Γ, całkowite pole powierzchni Riemanna jest równe polu standardowego wielokąta. Wzór na pole wynika z twierdzenia Gaussa – Bonneta i jest w pewnym sensie uogólniony wzorem Riemanna – Hurwitza .

Jawna forma dla standardowych wielokątów

Wyrażenia jawne można podać dla regularnego standardowego wielokąta o bokach 4 g , z symetrią obrotową. $\ displaystyle$ tym przypadku rodzaju powierzchni Riemanna z $g$ -krotną symetrią obrotową, grupa może być dana przez sol $}}$ . Te generatory są dane przez następujące ułamkowe transformaty liniowe działające na górną półpłaszczyznę :

{\ displaystyle a_{k}=\left({\begin{matrix}\cos k\alpha &-\sin k\alpha \\\sin k\alpha &\cos k\alpha \end{macierz}}\right)\ left({\begin{matrix}e^{p}&0\\0&e^{-p}\end{matrix}}\right)\left({\begin{matrix}\cos k\alpha &\sin k\ alpha \\-\sin k\alpha &\cos k\alpha \end{macierz}}\right)}

dla ${\ Displaystyle 0 \ równoważnik k <2g}$ . Parametry podaje wg

{\ Displaystyle \ alfa = {\ Frac {\ pi} {4g}} \ lewo (2g-1 \ ​​prawo)}

I

{\ Displaystyle \ beta = {\ Frac {\ pi} {4g}}}

I

{\ Displaystyle p = \ ln {\ Frac {\ sałata \ beta + {\ sqrt {\ sałata 2 \ beta}}} {\ sin \ beta}} }

Można zweryfikować, czy generatory te spełniają to ograniczenie

{\ Displaystyle a_ {0} a_ {1} \ cdots a_ {2g-1} a_ {0} ^ {-1}a_{1}^{-1}\cdots a_{2g-1}^{-1}=1}

co daje całość prezentacji grupy .

Zobacz też

Notatki

Ahlfors, Lars V. (2006), Wykłady o odwzorowaniach quasi-konformalnych , seria wykładów uniwersyteckich, tom. 38 (wyd. Drugie), Amerykańskie Towarzystwo Matematyczne , ISBN 978-0-8218-3644-6
Appell, P.; Goursat, E.; Fatou, P. (1930), Théorie des fonctions algébriques d'une variable, Tom II, Fonctions automorphes , Gauthier-Vi]lars, s. 102–154
Bambah, RP; Davenport, H. (1952), „Pokrycie n-wymiarowej przestrzeni sferami”, J. London Math. soc. , 27 (2): 224–229, doi : 10.1112/jlms/s1-27.2.224
Beardon, Alan F. (1983), Geometria grup dyskretnych , Springer-Verlag, ISBN 978-0-387-90788-8
Beardon, Alan F. (1984), Elementarz na powierzchniach Riemanna , London Mathematical Society Lecture Note Series, tom. 78, Cambridge University Press , ISBN 978-0-521-27104-2
Bonk, Mariusz; Schramm, Oded (2000), „Osadzenia przestrzeni hiperbolicznych Gromowa”, Geom. Funkcja Analny. , 10 (2): 266–306, CiteSeerX 10.1.1.47.7874 , doi : 10.1007/s000390050009
Böröczky, Károly, Jr. (2004), Skończone opakowanie i pokrycie , Cambridge Tracts in Mathematics, tom. 154, Cambridge University Press , ISBN 978-0-521-80157-7
Bourdon, Marc; Pajot, Hervé (2002), „Geometria quasikonformalna i geometria hiperboliczna”, w: Marc Burger; Alessandra Iozzi (red.), Sztywność w dynamice i geometrii , Springer, s. 1–17, ISBN 978-3-540-43243-2
Buser, Peter (1992), Geometria i widma zwartych powierzchni Riemanna , Progress in Mathematics, tom. 106, Birkäuser, doi : 10.1007/978-0-8176-4992-0 , ISBN 978-0-8176-3406-3
Cassels, JWS (1997), „IX. Opakowania”, Wprowadzenie do geometrii liczb , Klasyka matematyki , Springer-Verlag, ISBN 978-3-540-61788-4
Coxeter, HS M (1962), „Klasyfikacja zonohedry za pomocą diagramów rzutowych”, J. Math. Pures Appl. , 41 : 137–156
Coxeter, HSM ; Moser, WOJ (1980), Generatory i relacje dla grup dyskretnych , tom. 14 (wydanie czwarte. Ergebnisse der Mathematik und ihrer Grenzgebiete red.), Springer-Verlag, ISBN 978-3-540-09212-4
Eggleston, HG (1958), Convexity , Cambridge Tracts in Mathematics and Mathematical Physics, tom. Wydawnictwo Uniwersytetu Cambridge
Farb Benson ; Margalit, Dan (2012), Elementarz dotyczący mapowania grup klasowych , Princeton Mathematical Series, tom. 49, Princeton University Press , ISBN 978-0-691-14794-9
Farkas, Hershel M.; Kra, Irwin (1980), Powierzchnie Riemanna , Springer-Verlag, ISBN 978-0-387-90465-8
Fenchel, Werner ; Nielsen, Jakob (2003), Nieciągłe grupy izometrii w płaszczyźnie hiperbolicznej , de Gruyter Studies in Mathematics, tom. 29, Walter de Gruyter, ISBN 978-3-11-017526-4
Fricke, Robert; Klein, Felix (1897), Vorlesungen über die Theorie der automorphen Funktionen, Band 1: Die gruppentoretischen Grundlagen , Teubner, s. 236–237, 295–320
Grünbaum, Branko ; Shephard, GC (1987), Tilings i wzory , WH Freeman, ISBN 978-0-7167-1193-3
Guggenheimer, H. (1977), „Twierdzenie o krzywej Jordana i niepublikowany rękopis Maxa Dehna” (PDF) , Archiwum Historii Nauk Ścisłych , 17 (2): 193–200, CiteSeerX 10.1.1.374.1893 , doi : 10.1007/BF02464980 , JSTOR 41133486 , MR 0532231
Hirsch, Morris W. (1994), Topologia różniczkowa , Graduate Texts in Mathematics, tom. 33, Springer-Verlag, ISBN 978-0-387-90148-0
Imayoshi, Y.; Taniguchi, M. (1992), Wprowadzenie do przestrzeni Teichmüllera , Springer-Verlag, ISBN 978-0-387-70088-5
Iversen, Birger (1992), Geometria hiperboliczna , London Mathematical Society Student Texts, tom. 25, Cambridge University Press , ISBN 978-0-521-43508-6
Jost, Jurgen (2002), Compact Riemanna Surfaces (wyd. 2), Springer-Verlag, ISBN 978-3-540-43299-9
Kapowicz, Ilja; Benakli, Nadia (2002), „Granice grup hiperbolicznych”, Kombinatoryczna i geometryczna teoria grup , Contemp. Matematyka, tom. 296, Amerykańskie Towarzystwo Matematyczne , s. 39–93
Keen, Linda (1965), „Wielokąty kanoniczne dla skończenie generowanych grup fuchsowskich”, Acta Math. , 115 : 1–16, doi : 10.1007/bf02392200
Keen, Linda (1966), „Moduły wewnętrzne na powierzchniach Riemanna”, Ann. z matematyki. , 84 (3): 404–420, doi : 10.2307/1970454 , JSTOR 1970454
Kołmogorow, AN; Jukszkiewicz AP, wyd. (2001), Matematyka XIX wieku: logika matematyczna, algebra, teoria liczb, teoria prawdopodobieństwa , Springer, ISBN 978-3764364410
Lehto, Olli (1987), Funkcje jednowartościowe i przestrzenie Teichmüllera , Absolwent Teksty z matematyki, tom. 109, Springer-Verlag, ISBN 978-0-387-96310-5
Lyusternik, LA (1966), wypukłe figury i wielościany , przetłumaczone przez Donalda L. Barnetta, Boston: DC Heath and Co.
Nevanlinna, Rolf (1953), Uniformisierung , Die Grundlehren der Mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete (w języku niemieckim), tom. 64, Springer-Verlag
Seifert, Herbert; Threlfall, William (1934), Podręcznik topologii , Pure and Applied Mathematics, tom. 89, przetłumaczone przez Michaela A. Goldmana, Academic Press, ISBN 978-0-12-634850-7
Shastri, Anant R. (2011), Elementy topologii różniczkowej , CRC Press, ISBN 978-1-4398-3160-1
Siegel, CL (1971), Tematy z teorii funkcji zespolonych, tom. II. Funkcje automorficzne i całki abelowe w przekładzie A. Shenitzera; M. Tretkoff, Wiley-Interscience
Stillwell, John (1992), Geometria powierzchni , Universitext, Springer-Verlag, ISBN 978-0-387-97743-0
Zong, Chuanming (2014), „Pakowanie, pokrywanie i układanie płytek w przestrzeniach dwuwymiarowych”, Expositiones Mathematicae , 32 (4): 297–364, doi : 10.1016/j.exmath.2013.12.002