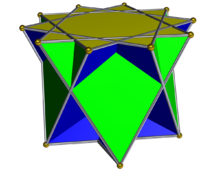
Skrzyżowana pentagramowa kopuła
| Skrzyżowana pentagramowa kopuła | |
|---|---|
 | |
| Typ |
Kopuła izomorficzna Johnsona |
| Twarze |
5 trójkątów 5 kwadratów 1 pentagram 1 dekagram |
| Krawędzie | 25 |
| Wierzchołki | 15 |
| Konfiguracja wierzchołków |
5+5(3.4.10/3) 5(3.4.5/3.4) |
| Symbol Schläfliego | {5/3} || t{5/3} |
| Grupa symetrii | C 5v , [5], (*55) |
| Grupa rotacyjna | do 5 , [5] + , (55) |
| Podwójny wielościan | - |
W geometrii skrzyżowana pentagramowa kopuła jest jedną z niewypukłych izomorficznych brył Johnsona , będąc topologicznie identyczną z wypukłą pięciokątną kopułą . Można go otrzymać jako wycinek wielkiego rombicosidodecahedron lub quasirhombicosidodecahedron. Jak we wszystkich kopułach wielokąt bazowy ma dwa razy więcej krawędzi i wierzchołków niż wierzchołek; w tym przypadku bazowym wielokątem jest dekagram .
Można go postrzegać jako kopułę z pentagramową podstawą wsteczną, tak że kwadraty i trójkąty łączą się w poprzek podstaw w sposób przeciwny do cuploidu pentagramowego , a tym samym przecinają się głębiej.
Powiązane wielościany
| nd _ _ | 4 | 5 | 7 | 8 |
|---|---|---|---|---|
| 3 |
 {4/3} |
 {5/3} |
 {7/3} |
 {8/3} |
| 5 | — | — |
 {7/5} |
 {8/5} |
Skrzyżowana pięciokątna kopuła może być postrzegana jako część jednorodnego wielościanu znanego jako niewypukły wielki rombozydodekahedron , wielki dwunastościan i wielki rombidodekaedr .
 Skrzyżowana pentagramowa kopuła |
 Niewypukły wielki rombicozydodekahedron |
 Wielki dwunastościan dwunastościanu |
 Wielki rombidodekaedr |
Różne skrzyżowane kopuły pentagramowe na niewypukłym wielkim rombikozydodekahedrze można zmniejszać lub obracać (obracać), aby uzyskać zestaw 12 wielościanów izomorficznych z bryłami Johnsona J 72 do J 83 . Są to gyrate, metabigyrate, parabigyrate, trigyrate, zmniejszony, metabidiminizowany, parabidiminowany, trydiminizowany, metagyrate zmniejszony, paragyrate zmniejszony, bigyrate zmniejszony i wirujący bidyminowany quasirhombicosidodecahedra.
Podwójny wielościan
Podwójna kopuła ze skrzyżowanymi pentagramami ma 10 trójkątnych i 5 latawców:
- Jim McNeill, Stosunek kopuł do jednolitych wielościanów
- Jim McNeill, Kopuła LUB Semicupola
- Richard Klitzing, Osiowo-symetryczne krawędzie ścianek jednolitych wielościanów
