Spirala stożkowa

Spirala stożkowa ze spiralą Archimedesa jako plan piętra

rzut kondygnacji: Spirala Fermata

plan piętra: spirala logarytmiczna

plan piętra: spirala hiperboliczna

W matematyce spirala stożkowa , znana również jako helisa stożkowa , jest krzywą przestrzenną na prawym okrągłym stożku , którego rzut jest płaską spiralą . Jeśli plan piętra jest spiralą logarytmiczną , nazywa się ją konchospiralną (od muszli ).

Reprezentacja parametryczna

W płaszczyźnie spirali z reprezentacją parametryczną ${\ displaystyle x}$ - ${\ displaystyle y}$

${\ Displaystyle x = r (\ varphi) \ cos \ varphi \ \ qquad y = r (\ varphi) \ sin \ varphi}$

trzecią współrzędną $dodać tak$$\displaystyle \;m^{2}(x^{2}+y^{2})=(z-z_{0})^{2}\ ,\ m>0\;}$ że krzywa przestrzenna leży $z$ równaniem ( :

• ${\ Displaystyle x = r (\ varphi) \ cos \ varphi \ \ qquad y = r (\ varphi) \ sin \ varphi \ \ qquad \ kolor {czerwony} {z = z_ {0} + mr (\ varphi )}\ .}$

Takie krzywe nazywane są spiralami stożkowymi. Byli znani Papposowi .

Parametr to nachylenie linii stożka względem płaszczyzny - $displaystyle$$x}$ - ${\ displaystyle y}$ .

Zamiast tego spiralę stożkową można postrzegać jako rzut prostopadły spirali planu piętra na stożek.

Przykłady

${\ Displaystyle x = a \ varphi \ cos \ varphi \ \ qquad y = a \ varphi \ sin \ varphi \ \ qquad z = z_ {0} + ma \ varphi \ \ quad \ varphi \ geq 0 \ . }$

) Rozpoczęcie od $)$ daje patrz

W tym przypadku spiralę stożkową można postrzegać jako krzywą przecięcia stożka z helikoidą .

$plan$ ) Drugi schemat Fermata jako

3) Trzeci przykład ma spiralę logarytmiczną ${\ Displaystyle \; r (\ varphi) = ae ^ {k \ varphi} \;}$ jako plan piętra. Jego cechą szczególną jest stałe nachylenie (patrz poniżej).

Wprowadzenie skrótu daje opis: $φ$${\ Displaystyle r (\ varphi) = aK ^$ varphi

4) Przykład 4 jest oparty na spirali hiperbolicznej ${\ Displaystyle \; r (\ varphi) = a/\ varphi \;}$ . Spirala taka ma asymptotę (linia czarna), która jest rzutem hiperboli ( kolor fioletowy). Spirala stożkowa zbliża się do hiperboli przez ${\ displaystyle \ varphi \ do 0}$ .

Nieruchomości

Poniższe badanie dotyczy stożkowych spiral w postaci odpowiednio $a \ varphi ^ {n}}$${\ displaystyle r = ae ^ {k \ varphi}}$ i .

Nachylenie

Kąt nachylenia w punkcie spirali stożkowej

Nachylenie w punkcie spirali stożkowej jest nachyleniem stycznej tego punktu względem płaszczyzny - $x}$ displaystyle - ${\ displaystyle y}$ . Odpowiedni kąt to kąt nachylenia (patrz schemat):

${\ Displaystyle \ tan \ beta = {\ Frac {z'} {\ sqrt {(x') ^ {2} + (y') ^ {2}}}} = {\ Frac {mr'} {\ sqrt {(r')^{2}+r^{2}}}}\ .}$

Spirala z ${\ displaystyle r = a \ varphi ^ {n}}$ daje:

• ${\ Displaystyle \ tan \ beta = {\ Frac {mn} {\ sqrt {n ^ {2} + \ varphi ^ {2}}}} \.}$

Ponieważ spirala Archimedesa wynosi ${\ Displaystyle n = 1}$ , a zatem jej nachylenie jest ${\ Displaystyle \ \ tan \ beta = {\ tfrac {m} {\ sqrt {1+ \ varphi ^ {2}}}} \.}$

• Dla $1$ logarytmicznej z nachyleniem jest $Displaystyle \ \ tan \ beta$ ( ${\ Displaystyle \ kolor {czerwony} {\ tekst {stała!}}})$ .

Ze względu na tę właściwość konchospirala nazywana jest równokątną spiralą stożkową.

Długość łuku

Długość łuku spirali stożkowej można określić za pomocą

${\ Displaystyle L = \ int _ {\ varphi _ {1}} ^ {\ varphi _ {2}} {\ sqrt {(x') ^ {2} + (y') ^ {2} + (z' )^{2}}}\,\mathrm {d} \varphi =\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(1+m^{2}) (r')^{2}+r^{2}}}\,\mathrm {d} \varphi \ .}$

Dla spirali Archimedesa całkę można rozwiązać za pomocą tablicy całek , analogicznie jak w przypadku planarnym:

${\ Displaystyle L = {\ Frac {a} {2}} {\ duży [} \ varphi {\ sqrt {(1 + m ^ {2}) + \ varphi ^ {2}}} + (1 + m ^ {2})\ln {\big (}\varphi +{\sqrt {(1+m^{2})+\varphi ^{2}}}{\big )}{\big ]}_{\varphi _{1}}^{\varphi_{2}}\ .}$

W przypadku spirali logarytmicznej całkę można łatwo rozwiązać:

${\ Displaystyle L = {\ Frac {\ sqrt {(1 + m ^ {2}) k ^ {2} + 1}} {k}} (r {\ duży (} \ varphi _ {2}) -r (\ varphi _ {1}) {\ duży )} \ .}$

W innych przypadkach występują całki eliptyczne .

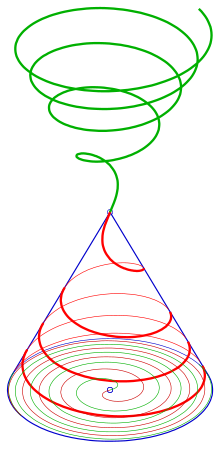
Rozwój

Rozwój (zielony) spirali stożkowej (czerwony), po prawej: widok z boku. Płaszczyzna zawierająca zabudowę została zaprojektowana przez ${\ displaystyle \ pi}$ . Początkowo stożek i płaszczyzna stykają się na fioletowej linii.

Dla rozwoju spirali stożkowej odległość $( ρ ($$\ Displaystyle \ rho (\ varphi)$ do wierzchołka stożka ${\ Displaystyle (0,0, z_ {0})}$ i związek między kątem $}$ odpowiednim kątem rozwoju należy określić: ${\ Displaystyle \ varphi$

${\ Displaystyle \ rho = {\ sqrt {x ^ {2} + y ^ {2} + (z-z_ {0} )^{2}}}={\sqrt {1+m^{2}}}\;r\ ,}$

${\ Displaystyle \ varphi = {\ sqrt {1 + m ^ {2}}} \ psi \.}$

Stąd biegunowa reprezentacja rozwiniętej spirali stożkowej to:

• ${\ Displaystyle \ rho (\ psi) = {\ sqrt {1 + m ^ {2}}} \; r ({\ sqrt {1 + m^{2}}}\psi )}$

W przypadku biegunowej reprezentacji opracowanej krzywej jest ${\ displaystyle r = a \ varphi ^ {n}}$

${\ Displaystyle \ rho = a {\ sqrt {1 + m ^ {2}}} ^ {\, n + 1} \ psi ^ {n},}$

który opisuje spiralę tego samego typu.

• Jeśli rzut stożkowej spirali jest spiralą Archimedesa , to jej rozwój jest spiralą Archimedesa.

W przypadku $)$ hiperbolicznej ( rozwój jest zgodny ze spiralą

W przypadku spirali logarytmicznej rozwój jest spiralą logarytmiczną: $\ Displaystyle r = ae ^ {k \ varphi}}$

${\ Displaystyle \ rho = a {\ sqrt {1 + m ^ {2}}} \; e ^ {k {\ sqrt {1 + m ^ {2}}} \ psi} \ .}$

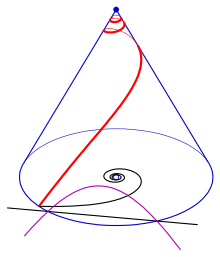
Ślad styczny

Ślad (fioletowy) stycznych spirali stożkowej ze spiralą hiperboliczną jako plan piętra. Czarna linia to asymptota spirali hiperbolicznej.

Zbiór punktów przecięcia stycznych spirali stożkowej z płaszczyzną $($ płaszczyzną $przechodzącą$ wierzchołek stożka) nazywa się jej śladem stycznym

Dla spirali stożkowej

${\ Displaystyle (r \ cos \ varphi, r \ sin \ varphi, mr)}$

wektor styczny jest

${\ Displaystyle (r '\ cos \ varphi -r \ sin \ varphi, r' \ sin \ varphi +r\cos \varphi ,mr')^{T}}$

i styczna:

${\ Displaystyle x (t) = r \ cos \ varphi + t (r '\ cos \ varphi -r \ sin \ varphi ) \ ,}$

${\ Displaystyle y (t) = r \ sin \ varphi + t (r '\ sin \varphi +r\cos \varphi )\ ,}$

${\ Displaystyle z (t) = pan + tmr '\ .}$

Punkt przecięcia z $y {\ Displaystyle$ ma parametr, $Displaystyle$ jest $x}$ y

• ${\ Displaystyle \ lewo ({\ Frac {r ^ {2}} {r'}} \ sin \ varphi, - {\ Frac {r ^ {2}} {r'}} \ cos \ varphi, 0 \ prawo )\ .}$

${\ Displaystyle r = a \ varphi ^ {n}}$ daje ${\ Displaystyle \ {\ tfrac {r ^ {2}} {r'}} = {\tfrac {a}{n}}\varphi ^{n+1}\ }$ a ślad styczny jest spiralą. W przypadku $hiperboliczna$ ) ślad styczny degeneruje się o promieniu $diagram$ . dla ${\ Displaystyle r = ae ^ {k \ varphi}}$ jeden ma ${\ Displaystyle \ {\ tfrac {r ^ {2}} {r'}} = { \tfrac {r}{k}}\ },$ a ślad styczny jest spiralą logarytmiczną, która jest przystająca do rzutu z powodu samopodobieństwa spirali logarytmicznej.

Muszle ślimaków ( Neptunea angulata po lewej, po prawej: Neptunea despecta

Linki zewnętrzne

• Jamnitzer -Galerie: 3D-Spiralen. .
• Weisstein, Eric W. „Spirala stożkowa” . MathWorld .