Spirala hiperboliczna

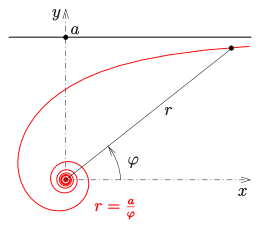
Spirala hiperboliczna: gałąź dla

φ > 0

Spirala hiperboliczna: obie gałęzie

Spirala hiperboliczna to płaska krzywa , którą można opisać równaniem we współrzędnych biegunowych

{\ Displaystyle R = {\ Frac {a} {\ varphi}}}

hiperboli . _ Ponieważ może być generowana przez odwrócenie okręgu spirali Archimedesa , nazywana jest również spiralą odwrotną .

Pierre Varignon po raz pierwszy zbadał krzywą w 1704 roku. Później nad krzywą pracowali również Johann Bernoulli i Roger Cotes .

Spirala hiperboliczna ma kąt nachylenia, który rośnie wraz z odległością od jej środka, w przeciwieństwie do spirali logarytmicznej (w której kąt jest stały) lub spirali Archimedesa (w której maleje wraz z odległością). Z tego powodu została wykorzystana do modelowania kształtów galaktyk spiralnych , które w niektórych przypadkach podobnie mają rosnący kąt nachylenia. Jednak ten model nie zapewnia dobrego dopasowania do kształtów wszystkich galaktyk spiralnych.

We współrzędnych kartezjańskich

spirala hiperboliczna z równaniem biegunowym

{\ Displaystyle R = {\ Frac {a} {\ varphi}}, \ quad \ varphi \ neq 0}

można przedstawić we współrzędnych kartezjańskich $(x = r cos φ, y = r sin φ)$ przez

\ Displaystyle x = a {\ Frac {\ cos \ varphi} {\ varphi}}, \ qquad y = a {\ frac { \sin \varphi }{\varphi }},\quad \varphi \neq 0.}

Hiperbola ma w płaszczyźnie $rφ$ osie współrzędnych jako asymptoty. Spirala hiperboliczna (w $xy$ ) zbliża się do $φ \to \pm\infty$ początku jako punkt asymptotyczny. Dla $φ \to \pm0$ krzywa ma linię asymptotyczną (patrz następna sekcja).

Z równania biegunowego i $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} φ = a / r , r = √ x 2 + y 2$ otrzymujemy reprezentację równaniem :

{\ Displaystyle {\ Frac {y} {x}} = \ tan \ lewo ({\ Frac {a} {\ sqrt {x ^ {2} + y ^ {2}}}} \ prawej).}

Właściwości geometryczne

Asymptota

Ponieważ

{\ Displaystyle \ lim _ {\ varphi \ do 0} x = a \ lim _ {\varphi \to 0}{\frac {\cos \varphi}{\varphi}}=\infty,\qquad \lim _{\varphi \to 0}y=a\lim _{\varphi \to 0} {\frac {\sin \varphi}} {\varphi}}=a}

krzywa ma asymptotę z równaniem $y = a$ .

Zbocze polarne

Definicja sektora (jasnoniebieski) i biegunowego kąta nachylenia

α

Z rachunku wektorowego we współrzędnych biegunowych otrzymuje się wzór $tan α = r' / r$ dla nachylenia biegunowego i jego kąta $α$ między styczną krzywej a styczną odpowiedniego koła biegunowego.

Dla spirali hiperbolicznej $r = a / φ$ nachylenie biegunowe wynosi

{\ Displaystyle \ tan \ alfa = - {\ Frac {1} {\ varphi}}.}

Krzywizna

Krzywizna krzywej o równaniu biegunowym $r = r (φ)$ wynosi

{\ Displaystyle \ kappa = {\ Frac {r ^ {2} + 2 (r ') ^ {2} - r \, r ''} {\ lewo (r ^ {2} + (r ') ^ {2 }\right)^{\frac {3}{2}}}}.}

Z równania $r = a / φ$ i pochodnych $r' = - a / φ 2$ i $r ″ = 2 a / φ 3$ otrzymujemy krzywiznę spirali hiperbolicznej:

{\ Displaystyle \ kappa (\ varphi) = {\ Frac {\ varphi ^ {4}} {a \ lewo (\ varphi ^ {2} + 1 \ prawo) ^ {\ Frac {3} {2}}}} .}

Długość łuku

Długość łuku spirali hiperbolicznej między $(r (φ 1), φ 1)$ a $(r (φ 2), φ 2)$ można obliczyć za pomocą całki:

{\ Displaystyle {\ rozpocząć {wyrównane} L & = \ int _ {\ varphi _ {1}} ^ {\ varphi _ {2}} {\ sqrt {\ lewo (r ^ {\ pierwsza} (\ varphi) \ prawo )^{2}+r^{2}(\varphi )}}\,d\varphi =\cdots \\&=a\int _{\varphi _{1}}^{\varphi _{2}} {\frac {\sqrt {1+\varphi ^{2}}}{\varphi ^{2}}}\,d\varphi \\&=a\left[-{\frac {\sqrt {1+\ varphi ^{2}}}{\varphi }}+\ln \left(\varphi +{\sqrt {1+\varphi ^{2}}}\right)\right]_{\varphi _{1}} ^{\varphi _{2}}.\end{wyrównane}}}

Obszar sektora

Obszar sektora (patrz diagram powyżej) spirali hiperbolicznej o równaniu $r = a / φ$ wynosi:

{\ Displaystyle {\ rozpocząć {wyrównane} A & = {\ Frac {1} {2}} \ int _ {\ varphi _ {1}} ^ {\ varphi _ {2}} r (\ varphi) ^ {2} \,d\varphi \\&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\frac {a^{2}}{ \varphi ^{2}}}\,d\varphi \\&={\frac {a}{2}}\left({\frac {a}{\varphi _{1}}}-{\frac { a}{\varphi _{2}}}\right)\\&={\frac {a}{2}}{\bigl (}r(\varphi _{1})-r(\varphi _{2 }){\bigr )}.\end{wyrównane}}}

Inwersja

Spirala hiperboliczna (niebieska) jako obraz spirali Archimedesa (zielona) z odwróceniem koła

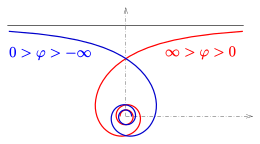
Inwersja na okręgu jednostkowym ma we współrzędnych biegunowych prosty opis: $(r, φ) \mapsto (1 / r, φ)$ .

Obrazem spirali Archimedesa $r = φ / a$ z odwróceniem koła jest spirala hiperboliczna o równaniu $r = a / φ$ . Przy $φ = a$ obie krzywe przecinają się w stałym punkcie na okręgu jednostkowym.

Oscylujący okrąg spirali Archimedesa $r = φ / a$ na początku ma promień $0 ρ = 1 / 2 a$ ( patrz spirala Archimedesa ) i środek $00 ( , ρ)$ . Obrazem tego okręgu jest linia $y = a$ (patrz odwrócenie okręgu ). Stąd preobrazem asymptoty spirali hiperbolicznej z odwróceniem spirali Archimedesa jest oscylujący okrąg spirali Archimedesa na początku.

Przykład: Diagram pokazuje przykład z

a = π

.

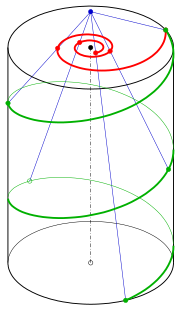
Środkowa projekcja helisy

Spirala hiperboliczna jako centralny rzut helisy

Rozważmy centralny rzut z punktu $0 C = (0, 0, d)$ na płaszczyznę obrazu $z = 0$ . Spowoduje to odwzorowanie punktu $(x, y, z)$ na punkt $d / d - z (x, y)$ .

Obraz pod tą projekcją helisy z reprezentacją parametryczną

{\ Displaystyle (r \ cos t, r \ sin t, ct), \ quad c \ neq 0,}

jest krzywą

{\ Displaystyle {\ Frac {dr} {d-ct}} (\ sałata t, \ grzech t)}

z równaniem biegunowym

{\ Displaystyle \ rho = {\ Frac {dr} {d-ct}}}

który opisuje spiralę hiperboliczną.

Dla parametru $0 t = d / c$ spirala hiperboliczna ma biegun, a helisa przecina płaszczyznę $z = d$ w punkcie $V 0$ . Można sprawdzić za pomocą obliczeń, że obraz helisy zbliżającej się do $V 0$ jest asymptotą spirali hiperbolicznej.

Hans-Jochen Bartsch, Michael Sachs: Taschenbuch mathematischer Formeln für Ingenieure und Naturwissenschaftler , Carl Hanser Verlag, 2018, ISBN 3446457070 , 9783446457072, S. 410.
Kinko Tsuji, Stefan C. Müller: Spirale i wiry: w kulturze, naturze i nauce , Springer, 2019, ISBN 3030057984 , 9783030057985, S. 96.
Pierre Varignon: Nouvelle formation de Spirales – przykład II , Mémoires de l'Académie des sciences de l'Institut de France, 1704, s. 94–103.
Friedrich Grelle: Analytische Geometrie der Ebene , Verlag F. Brecke, 1861 hyperbolische Spirale , S. 215.
Jakob Philipp Kulik : Lehrbuch der höhern Analysis, Band 2 , In Commiss. bei Kronberger u. Rziwnatz, 1844, Spirallinien , S. 222.

Linki zewnętrzne