Lista spirali

Ta lista spiral zawiera nazwane spirale , które zostały opisane matematycznie.

Obraz	Nazwa	Pierwszy opisany	Równanie	Komentarz
	koło		${\ displaystyle r = k}$	Trywialna spirala
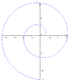
	Spirala Archimedesa	C. 320 pne	${\ Displaystyle r = a + b \ cdot \ teta}$	Znana również jako spirala arytmetyczna
	Spirala Eulera (także spirala Cornu lub spirala wielomianowa)		${\ Displaystyle x (t) = \ nazwa operatora {C} (t), \,} r$$\ Displaystyle y (t) = \ nazwa operatora {S} (t)}$	za pomocą całek Fresnela
	Spirala Fermata (także paraboliczna)	1636	${\ Displaystyle r ^ {2} = a ^ {2} \ cdot \ theta}$
	spirala hiperboliczna	1704	${\ Displaystyle R = {\ Frac {a} {\ teta}}}$	również wzajemna spirala
	Lituus	1722	${\ Displaystyle r ^ {2} \ cdot \ teta = k}$
	spirala logarytmiczna	1638	${\ Displaystyle R = a \ cdot e ^ {b \ cdot \ teta}}$	Przybliżenia tego można znaleźć w naturze; znany również jako równokątna spirala.
	Spirala Fibonacciego		łuki kołowe łączące przeciwległe rogi kwadratów w układzie Fibonacciego	przybliżenie złotej spirali
	złota spirala		${\ Displaystyle R = \ varphi ^ {\ Frac {2 \ cdot \ teta} {\ pi}} \,}$	szczególny przypadek spirali logarytmicznej
	Spirala Teodora			Znana również jako spirala Pitagorasa; wielokątna spirala złożona z przylegających do siebie trójkątów prostokątnych, która jest zbliżona do spirali Archimedesa
	spiralny	1673
	spirala		${\ Displaystyle r (t) = 1 \,}$${\ Displaystyle \ teta (t) = t \,}$${\ Displaystyle z(t)=t}$	trójwymiarowa spirala
	Linia Rhumb (także loxodrome)			rodzaj spirali narysowanej na kuli
	Spirala Cotesa	1722	${\ Displaystyle {\ Frac {1} {r}} = {\ rozpocząć {przypadki} A \ cosh (k \ theta + \ varepsilon) \\ A \ exp (k \ theta + \ varepsilon) \\ A \ sinh ( k\theta +\varepsilon )\\A(k\theta +\varepsilon )\\A\cos(k\theta +\varepsilon )\\\end{przypadki}}}$	Rozwiązanie problemu dwóch ciał dla siły centralnej odwróconego sześcianu
	Spirale Poinsota		${\ Displaystyle r = a \ cdot \ operatorname {csch} (n \ cdot \ theta), \,}$${\ Displaystyle r=a\cdot \nazwa_operatora {sech} (n\cdot \theta )}$
	Spirala Nielsena	1993	${\ Displaystyle x (t) = \ operatorname {ci} (t), \,}$${\ Displaystyle y (t) = \ nazwa operatora {si} (t)}$	Odmiana spirali Eulera wykorzystująca całki sinusoidalne i cosinusoidalne
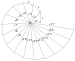
	Spirala wieloboczna			specjalny przypadek przybliżenia spirali logarytmicznej
	Spirala Frasera	1908		Złudzenie optyczne oparte na spiralach
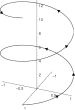
	konchospiralny		${\ Displaystyle r = \ mu ^ {t} \ cdot a, \,}$${\ Displaystyle \ teta = t, \,}$${\ Displaystyle z =\mu ^{t}\cdot c}$	trójwymiarowa spirala na powierzchni stożka.
	Spirala Calkina-Wilfa
	Spirala Ulama (również pierwsza spirala)	1963
	Spirala Sacka	1994		wariant spirali Ulama i spirali Archimedesa.
	Spirala Seifferta	2000	${\ Displaystyle R = \ nazwa operatora {sn} (s, k), \,}$${\ Displaystyle \ theta = k \ cdot s}$${\ Displaystyle Z = \ nazwa operatora {cn} (s, k)}$	krzywa spiralna na powierzchni kuli za pomocą funkcji eliptycznych Jacobiego
	Spirala Tractrixa	1704	${\ Displaystyle {\ rozpocząć {przypadki} r = A \ cos (t) \\\ teta = \ tan (t) -t \ koniec { sprawy}}}$
	Spirala Pappusa	1779	${\ Displaystyle {\ rozpocząć {przypadki} r = a \ teta \\\ psi = k \ koniec {przypadków}}}$	Spirala stożkowa 3D badana przez Pappusa i Pascala
	spirala dopplerowska		${\ Displaystyle x = a \ cdot (t \ cdot \ cos (t) + k \ cdot t), \,}$${\ Displaystyle y = a \ cdot t \ cdot \ sin (t)}$	Projekcja 2D spirali Pappus
	Spirala Atzemy		${\ Displaystyle x = {\ Frac {\ sin (t)} {t}} -2 \ cdot \ sałata (t)-t\cdot \sin(t),\,}$${\ Displaystyle y = - {\ Frac {\ cos (t)} {t}} -2 \ cdot \ sin (t) + t \ cdot \ cos (t)}$	Krzywa z katakaustyką tworzącą okrąg. Przybliża spiralę Archimedesa.
	Spirala atomowa	2002	${\ Displaystyle R = {\ Frac {\ teta} {\ teta -a}}}$	Ta spirala ma dwie asymptoty ; jeden to okrąg o promieniu 1, a drugi to linia ${\ displaystyle \ theta = a}$
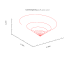
	Spirala galaktyczna	2019	${\ Displaystyle {\ rozpocząć {przypadki} dx = R * {\ Frac {y} {\ sqrt {x ^ {2} + y ^ {2}}}} d \ theta \\ dy = R * {\ Bigl [ }\rho (\theta )-{\frac {x}{\sqrt {x^{2}+y^{2}}}}{\Bigr ]}d\theta \end{przypadki}}{\begin{ przypadki}x=\suma dx\\\\\\y=\suma dy+R\end{przypadki}}}$	Różniczkowe równania spiralne zostały opracowane w celu symulacji ramion spiralnych galaktyk dyskowych, mają 4 rozwiązania w trzech różnych przypadkach: ${\ Displaystyle \ rho <1, \ rho = 1, \ rho > 1}$ o spiralnych wzorach decyduje zachowanie parametru ${\ displaystyle \ rho}$ . ρ ${\ Displaystyle \ rho <1}$ , spiralny wzór pierścienia ${\ displaystyle \ rho = 1,}$ regularna spirala; ${\ Displaystyle \ rho > 1,}$ luźna spirala. R to odległość punktu początkowego spirali (0, R) od środka. Obliczone x i y należy obrócić wstecz o $($ ) w celu Proszę sprawdzić referencje dla szczegółów

Zobacz też

• Koło Katarzyny (fajerwerk)
• Lista galaktyk spiralnych
• Spirala Parkera
• spirala
• spirograf