Spirala Fermata

Spirala Fermata: jedna gałąź

Spirala Fermata: obie gałęzie

Spirala Fermata lub spirala paraboliczna jest krzywą płaską , której właściwość polega na tym, że obszar między dowolnymi dwoma kolejnymi pełnymi zwojami wokół spirali jest niezmienny. W rezultacie odległość między zwojami rośnie odwrotnie proporcjonalnie do ich odległości od środka spirali, w przeciwieństwie do spirali Archimedesa (dla której odległość ta jest niezmienna) i spirali logarytmicznej (dla której odległość między zwojami jest proporcjonalna do odległości od Centrum). Spirale Fermata zostały nazwane na cześć Pierre'a de Fermata .

Ich zastosowania obejmują ciągłe mieszanie krzywizn krzywych, modelowanie wzrostu roślin i kształtów niektórych galaktyk spiralnych oraz projektowanie kondensatorów zmiennych , układów reflektorów energii słonecznej i cyklotronów .

Reprezentacja współrzędnych

Polarny

Reprezentacja spirali Fermata we współrzędnych biegunowych jest dana równaniem ${\ Displaystyle (r, \ varphi)}$

$${\ Displaystyle R = \ pm a {\ sqrt {\ varphi}}}$$

dla ${\ Displaystyle \ varphi \ geq 0}$ . Dwa wybory znaku dają dwie gałęzie spirali, które płynnie spotykają się na początku. Gdyby te same zmienne zostały ponownie zinterpretowane jako współrzędne kartezjańskie , byłoby to równanie paraboli z osią poziomą, która ponownie ma dwie gałęzie powyżej i poniżej osi, spotykające się w początku.

kartezjański

Spiralę Fermata z równaniem biegunowym można przekonwertować na współrzędne kartezjańskie ${\ Displaystyle (x, y)}$ za pomocą standardowego r = za ${\ varphi}}}$${\ Displaystyle x = r \ cos \ varphi}$ sałata i ${\ Displaystyle y = r \ sin \ varphi$ . Użycie równania biegunowego dla spirali w celu wyeliminowania z tych konwersji daje równania parametryczne dla krzywej: ${\ displaystyle r}$

$$\ Displaystyle {\ rozpocząć {wyrównane} x & = a {\ sqrt {\ varphi}} \ bo \ varphi \\ y & = a {\ sqrt {\ varphi }}\sin \varphi ,\\\end{wyrównane}}}$$

które generują punkty jednej gałęzi krzywej, gdy parametr $.$ się w dodatnich liczbach rzeczywistych

Dla dowolnego $}$ w ten sposób podziału $}}$ y $\ Displaystyle y$$anuluje$ się za ${\ textstyle a {\$ części równań parametrycznych, pozostawiając prostsze równanie ${\ Displaystyle {\ tfrac {x} {y}} = \ cot \ lewo (\ varphi \ prawej)}$ . Z tego równania, zastępując $}$ przeorganizowaną równania biegunowego dla spirali) $varphi$ a następnie podstawienie przez (konwersja z kartezjańskiego na biegunowy) pozostawia $=$$^ {2}}}}$ równanie dla spirali Fermata w kategoriach tylko i ${\ displaystyle y}$ : ${\ displaystyle x}$

$${\ Displaystyle {\ Frac {x} {y}} = \ łóżeczko \ lewo ({\ Frac {x ^ {2} + y ^ {2}} {a ^ {2}}} \ prawo).}$$

Ponieważ znak jest tracony $, gdy jest$ do kwadratu, to równanie obejmuje obie gałęzie krzywej.

Właściwości geometryczne

Spirala Fermata dzieli płaszczyznę na dwa połączone regiony (schemat: czarno-biały)

Podział samolotu

Kompletna spirala Fermata (obie gałęzie) jest gładką krzywą bez punktów podwójnych , w przeciwieństwie do spirali Archimedesa i spirali hiperbolicznej . Podobnie jak linia, okrąg lub parabola, dzieli płaszczyznę na dwa połączone regiony.

Definicja sektora (jasnoniebieski) i biegunowego kąta nachylenia α

Zbocze polarne

Z rachunku wektorowego we współrzędnych biegunowych otrzymuje się wzór

${\ Displaystyle \ dębnik \ alfa = {\ Frac {r'} {r}}}$

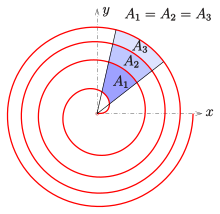
dla nachylenia biegunowego i jego kąta α między styczną krzywej a odpowiednim kołem biegunowym (patrz diagram).

Dla spirali Fermata r = a √ φ otrzymujemy

${\ Displaystyle \ tan \ alfa = {\ Frac {1} {2 \ varphi}}.}$

Stąd kąt nachylenia maleje monotonicznie.

Krzywizna

Z formuły

${\ Displaystyle \ kappa = {\ Frac {r ^ {2} + 2 (r ') ^ { 2}-r\,r''}{\left(r^{2}+(r')^{2}\right)^{\frac {3}{2}}}}}$

dla krzywizny krzywej z równaniem biegunowym r = r ( φ ) i jego pochodnymi

$\ Displaystyle {\ rozpocząć {wyrównane} r '& = {\ tfrac {a} {2 {\ sqrt {\varphi}}}}={\tfrac {a^{2}}{2r}}\\r''&=-{\tfrac {a}{4{\sqrt {\varphi}}^{3} }}=-{\tfrac {a^{4}}{4r^{3}}}\end{wyrównane}}}$

otrzymuje się krzywiznę spirali Fermata:

$${\ Displaystyle \ kappa (r) = {\ Frac {2r \ lewo (4r ^ {4} + 3a ^ {4} \ prawo)} {\ lewo (4r ^ {4} + a ^ {2} \ prawo) ^{\frac {3}{2}}}}.}$$

Na początku krzywizna wynosi 0. Stąd cała krzywa ma na początku punkt przegięcia , a oś x jest tam styczna.

Obszar między łukami

Pole wycinka spirali Fermata między dwoma punktami ( r ( φ ₁ ), φ ₁ ) i ( r ( φ ₂ ), φ ₂ ) wynosi

${\ Displaystyle {\ rozpocząć {wyrównane} {\ podkreślenie {A}} & = {\ Frac {1} {2}} \ int _ {\ varphi _ {1}} ^ {\ varphi _ {2}} r ( \varphi )^{2}\,d\varphi \\&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}a^{2 }\varphi \,d\varphi \\&={\frac {a^{2}}{4}}\left(\varphi _{2}^{2}-\varphi _{1}^{2} \right)\\&={\frac {a^{2}}{4}}\left(\varphi _{2}+\varphi _{1}\right)\left(\varphi _{2}- \varphi _{1}\right).\end{wyrównane}}}$

Spirala Fermata: obszar między sąsiednimi łukami

Po podniesieniu obu kątów o 2 π otrzymujemy

${\ Displaystyle {\ overline {A}} = {\ Frac {a ^ {2}} {4}} \ lewo (\ varphi _ {2} + \ varphi _ {1} + 4 \ pi \ prawo) \ lewo (\varphi _{2}-\varphi _{1}\right)={\podkreślenie {A}}+a^{2}\pi \left(\varphi _{2}-\varphi _{1}\ Prawidłowy).}$

Stąd obszar A regionu między dwoma sąsiednimi łukami wynosi

$${\ Displaystyle A = a ^ {2} \ pi \ lewo (\ varphi _ {2} - \ varphi _ {1} \ prawo).}$$

A zależy tylko od różnicy dwóch kątów, a nie od samych kątów.

W przykładzie pokazanym na schemacie wszystkie sąsiednie paski mają takie samo pole: A ₁ = A ₂ = A ₃ .

Ta właściwość jest wykorzystywana w elektrotechnice do budowy kondensatorów zmiennych .

regiony pomiędzy nimi (biały, niebieski, żółty) mają taki sam obszar, który jest równy polu narysowanego koła.

Przypadek szczególny ze względu na Fermata

W 1636 roku Fermat napisał list do Marina Mersenne , który zawiera następujący szczególny przypadek:

Niech φ ₁ = 0, φ ₂ = 2 π ; wówczas pole czarnego obszaru (patrz diagram) wynosi ₀ A = a ² π ² , co stanowi połowę pola koła K ₀ o promieniu r (2 π ) . Obszary pomiędzy sąsiednimi krzywymi (biały, niebieski, żółty) mają takie samo pole A = 2 a ² π ² . Stąd:

• Pole między dwoma łukami spirali po pełnym obrocie jest równe polu koła K ₀ .

Długość łuku

Długość łuku spirali Fermata między dwoma punktami ( r ( φ _i ), φ _i ) można obliczyć z całki :

${\ Displaystyle {\ rozpocząć {wyrównane} L & = \ int _ {\ varphi _ {1}} ^ {\ varphi _ {2}} {\ sqrt {\ lewo (r ^ {\ pierwsza} (\ varphi) \ prawo )^{2}+r^{2}(\varphi )}}\,d\varphi =\cdots \\&={\frac {a}{2}}\int _{\varphi _{1}} ^{\varphi _{2}}{\sqrt {{\frac {1}{\varphi}}+4\varphi}}\,d\varphi .\end{wyrównane}}}$

Ta całka prowadzi do całki eliptycznej , którą można rozwiązać numerycznie.

$za$ Fermata funkcji i niekompletna funkcja beta ${\ Displaystyle \ nazwa operatora {B} \ lewo (z; \, a; \,b\prawo)}$ :

${\ Displaystyle {\ rozpocząć {wyrównane} L & = a \ cdot {\ sqrt {\ varphi}} \ cdot \ nazwa operatora {_ {2} F_ {1}} \ lewo (- {\ frac {1} {2}} ,\,{\frac {1}{4}};\,{\frac {5}{4}};\,-4\cdot \varphi ^{2}\right)\\&=a\cdot { \frac {1-i}{8}}\cdot \operatorname {B} \left(-4\cdot \varphi ^{2};\,{\frac {1}{4}},\,{\frac {3}{2}}\prawo)\\\koniec{wyrównany}}}$

Odwrócenie spirali Fermata (zielona) to spirala lituusa (niebieska)

Odwrócenie koła

Inwersja na okręgu jednostkowym ma we współrzędnych biegunowych opis prosty ( r , φ ) ↦ ( 1 / r , φ ) .

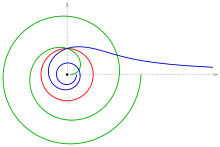
• Obrazem spirali Fermata r = a √ φ pod inwersją na okręgu jednostkowym jest spirala lituusa z równaniem biegunowym
  $${\ Displaystyle \; r = {\ Frac {1} {a {\ sqrt {\ varphi}}}}.}$$
  Gdy φ = 1 / a ² , obie krzywe przecinają się w stałym punkcie na okręgu jednostkowym.
• Styczna ( oś x ) w punkcie przegięcia (początku) spirali Fermata jest odwzorowywana na siebie i jest linią asymptotyczną spirali lituusa.

Złoty podział i złoty kąt

W filotaksji dyskowej , podobnie jak u słonecznika i stokrotki, siatka spiral występuje w liczbach Fibonacciego , ponieważ dywergencja (kąt następstwa w układzie pojedynczej spirali) zbliża się do złotego podziału . Kształt spiral zależy od wzrostu elementów generowanych sekwencyjnie. filotaksji dojrzałych dysków , gdy wszystkie elementy są tego samego rozmiaru, kształt spirali jest idealny dla spirali Fermata. To dlatego, że spirala Fermata przecina równe pierścienie w równych obrotach. Pełny model zaproponowany przez H. Vogla w 1979 r. to

${\ Displaystyle {\ rozpocząć {wyrównane} r & = c {\ sqrt {n}}, \\\ teta & = n \ razy 137,508 ^ {\ circ}, \ koniec {wyrównany}}}$

gdzie θ to kąt, r to promień lub odległość od środka, a n to numer indeksu różyczki, a c to stały współczynnik skalowania. Kąt 137,508° jest złotym kątem , który jest przybliżony stosunkami liczb Fibonacciego .

Wzór różyczek wyprodukowany przez model Vogel's (środkowy obraz). Pozostałe dwa obrazy przedstawiają wzorce dla nieco innych wartości kąta.

Powstały w ten sposób spiralny układ dysków jednostkowych należy odróżnić od spiral Doyle'a , czyli układów tworzonych przez styczne dyski o geometrycznie rosnących promieniach umieszczone na spiralach logarytmicznych .

Rośliny słoneczne

Stwierdzono również, że spirala Fermata jest wydajnym układem luster skoncentrowanych elektrowni słonecznych .

Zobacz też

• Lista spirali
• Wzory w przyrodzie
• Spirala Teodora

Dalsza lektura

•   J. Dennis Lawrence (1972). Katalog specjalnych krzywych płaskich . Publikacje Dover. s. 31, 186 . ISBN 0-486-60288-5 .

Linki zewnętrzne

• „spirala Fermata” . Encyklopedia matematyki . EMS Naciśnij . 2001 [1994].
• Eksploracja online przy użyciu JSXGraph (JavaScript)
• Spirale naturalne Fermata, w sciencenews.org