Punkt Fermata

Ryc. 1. Budowa pierwszego centrum izogonicznego, X(13). Kiedy żaden kąt trójkąta nie przekracza 120°, ten punkt jest punktem Fermata.

W geometrii euklidesowej punkt Fermata trójkąta , zwany także punktem Torricellego lub punktem Fermata-Torricellego , jest takim punktem, że suma trzech odległości od każdego z trzech wierzchołków trójkąta do punktu jest najmniejszą możliwą lub , równoważnie, mediana geometryczna trzech wierzchołków. Został tak nazwany, ponieważ problem ten został po raz pierwszy podniesiony przez Fermata w prywatnym liście do Evangelista Torricelli , który go rozwiązał.

Punkt Fermata daje rozwiązanie problemów z medianą geometryczną i drzewem Steinera dla trzech punktów.

Budowa

Punkt Fermata trójkąta o największym kącie co najwyżej 120° jest po prostu jego pierwszym izogonicznym środkiem lub X(13) , który jest zbudowany w następujący sposób:

1. Skonstruuj trójkąt równoboczny na każdym z dwóch dowolnie wybranych boków danego trójkąta.
2. Narysuj linię od każdego nowego wierzchołka do przeciwległego wierzchołka oryginalnego trójkąta.
3. Dwie proste przecinają się w punkcie Fermata.

Alternatywna metoda jest następująca:

1. Na każdym z dwóch dowolnie wybranych boków skonstruuj trójkąt równoramienny o podstawie tego boku, kątach 30 stopni u podstawy i trzecim wierzchołku każdego trójkąta równoramiennego leżącego poza pierwotnym trójkątem.
2. Dla każdego trójkąta równoramiennego narysuj okrąg, w każdym przypadku ze środkiem w nowym wierzchołku trójkąta równoramiennego io promieniu równym każdemu z dwóch nowych boków tego trójkąta równoramiennego.
3. Przecięcie wewnątrz pierwotnego trójkąta między dwoma okręgami to punkt Fermata.

Gdy trójkąt ma kąt większy niż 120°, punkt Fermata znajduje się w wierzchołku rozwartokątnym.

W dalszej części „Przypadek 1” oznacza, że ​​trójkąt ma kąt przekraczający 120°. „Przypadek 2” oznacza, że ​​żaden kąt trójkąta nie przekracza 120°.

Lokalizacja X(13)

Rys. 2. Geometria pierwszego środka izogonicznego.

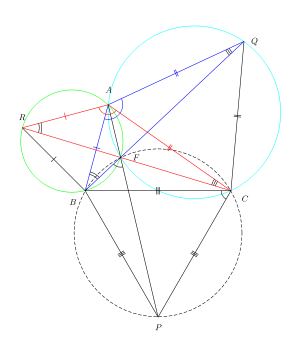
Ryc. 2 przedstawia trójkąty równoboczne △ ARB , △ AQC , △ CPB dołączone do boków dowolnego trójkąta △ ABC . Oto dowód wykorzystujący właściwości punktów koncyklicznych , aby pokazać, że trzy proste RC, BQ, AP na ryc. 2 przecinają się w punkcie F i przecinają się pod kątem 60°.

Trójkąty △ RAC , △ BAQ są przystające , ponieważ drugi jest obrotem pierwszego o 60° względem A . Stąd ∠ ARF = ∠ ABF i ∠ AQF = ∠ ACF . Przez odwrotność twierdzenia o kącie wpisanym zastosowanego do odcinka AF , punkty ARBF są koncykliczne (leżą na okręgu). Podobnie punkty AFCQ są koncykliczne.

∠ARB o 60° = ∠AFB = 120° , więc , korzystając z twierdzenia kącie wpisanym . Podobnie ∠ AFC = 120° .

Więc ∠ BFC = 120° . Dlatego ∠ BFC + ∠ BPC = 180° . Korzystając z twierdzenia o kącie wpisanym , oznacza to, że punkty BPCF są koncykliczne. Zatem, korzystając z twierdzenia o kącie wpisanym zastosowanego do odcinka BP , ∠ BFP = ∠ BCP = 60° . Ponieważ ∠ BFP + ∠ BFA = 180° , punkt F leży na odcinku AP . Zatem proste RC, BQ, AP są współbieżne (przecinają się w jednym punkcie). CO BYŁO DO OKAZANIA

Dowód ten ma zastosowanie tylko w Przypadku 2, ponieważ jeśli ∠ BAC > 120° , punkt A leży wewnątrz okręgu opisanego na △ BPC , który zamienia względne położenia A i F . Jednak można go łatwo zmodyfikować, aby obejmował Przypadek 1. Wtedy ∠ AFB = ∠ AFC = 60° stąd ∠ BFC = ∠ AFB + ∠ AFC = 120° , co oznacza, że ​​BPCF jest koncykliczny, więc ∠ BFP = ∠ BCP = 60° = ∠ BFA . Zatem A leży na FP .

Linie łączące środki okręgów na rys. 2 są prostopadłe do odcinków AP , BQ , CR . Na przykład linia łącząca środek okręgu zawierającego △ ARB i środek okręgu zawierającego △ AQC , jest prostopadła do odcinka AP . Zatem linie łączące środki okręgów również przecinają się pod kątem 60°. Dlatego środki okręgów tworzą trójkąt równoboczny. Jest to znane jako twierdzenie Napoleona .

Lokalizacja punktu Fermata

Tradycyjna geometria

Rys. 3. Geometria punktu Fermata

Biorąc pod uwagę dowolny trójkąt euklidesowy △ ABC i dowolny punkt P niech ${\ Displaystyle d (P) =| PA|+|PB|+|PC|.}$ Celem tej sekcji jest zidentyfikowanie punktu P ₀ takiego, że ${\ Displaystyle d (P_ { 0})<d(P)}$ dla wszystkich ${\ Displaystyle P \ neq P_ {0}.}$ Jeśli taki punkt istnieje, będzie to punkt Fermata. W dalszej części Δ będzie oznaczać punkty wewnątrz trójkąta i zostanie przyjęte, że zawiera jego granicę Ω .

Kluczowym wynikiem, który zostanie zastosowany, jest reguła dogleg, która zapewnia, że ​​jeśli trójkąt i wielokąt mają jeden wspólny bok, a reszta trójkąta leży wewnątrz wielokąta, to trójkąt ma krótszy obwód niż wielokąt:

Jeśli AB jest wspólnym bokiem, przedłuż AC , aby przeciąć wielokąt w punkcie X . Wtedy obwód wielokąta jest równy nierówności trójkąta :

${\ Displaystyle {\ tekst {obwód}}>| AB | + | AX | + | XB | = | AB | + | AC | + | CX | + | XB | \ geq | AB | + | AC | + | pne |.}$

Niech P będzie dowolnym punktem na zewnątrz Δ . Powiąż każdy wierzchołek z jego odległą strefą; to znaczy półpłaszczyzna poza (rozciągniętą) przeciwną stroną. Te 3 strefy obejmują całą płaszczyznę z wyjątkiem samego Δ , a P wyraźnie leży w jednej lub dwóch z nich. Jeśli P jest na dwie $( P')=d(A)<d(P)}$ (powiedzmy przecięcie stref B i C) to ustawienie implikuje ( $re$ według reguły dogleg. $to$ jeśli P znajduje w jednej strefie, powiedzmy A , gdzie P przecięciem BC . Zatem dla każdego punktu P na zewnątrz Δ istnieje punkt P' w Ω taki, że ${\ Displaystyle d (P ') <d (P).}$

Przypadek 1. Trójkąt ma kąt ≥ 120°.

Bez utraty ogólności załóżmy, że kąt w A wynosi ≥ 120°. Skonstruuj trójkąt równoboczny △ AFB i dla dowolnego punktu P w Δ (oprócz samego A ) skonstruuj Q tak, aby trójkąt △ AQP był równoboczny i miał pokazaną orientację. Wtedy trójkąt △ ABP jest obrócony o 60° trójkąta △ AFQ wokół A , więc te dwa trójkąty są przystające i wynika z tego, że ${\ Displaystyle d (P) =|CP|+|PQ|+|QF|},$ który jest po prostu długością ścieżki CPQF . Ponieważ P jest ograniczone do leżenia w △ ABC , zgodnie z regułą dogleg długość tej ścieżki przekracza ${\ Displaystyle | AC|+|AF|=d (A).}$ Dlatego ${\ Displaystyle d (A) <d (P)}$ dla wszystkich ${\ Displaystyle P \ in \ Delta, P \ neq A.}$ Teraz pozwól P na zakres poza Δ . $P '\ in \ Omega}$ ∈ ${\ Displaystyle d (A) \ równoważnik d (P')}$ istnieje tak, że ${\ Displaystyle d (P') <d (P)}$ i jako wynika, że ${\ Displaystyle d (A) <d (P)}$ dla wszystkich P. na zewnątrz Δ . Zatem $)}$$P$ dla wszystkich oznacza, że ​​A jest punktem Fermata Δ . Innymi słowy, punkt Fermata leży w wierzchołku rozwartokątnym .

Przypadek 2. Trójkąt nie ma kąta ≥ 120°.

Skonstruuj trójkąt równoboczny △ BCD , niech P będzie dowolnym punktem wewnątrz Δ i skonstruuj trójkąt równoboczny △ CPQ . Wtedy △ CQD jest obrotem △ CPB o 60° wokół C tak

${\ Displaystyle d (P) =|PA|+|PB|+|PC|=|AP|+|PQ|+|QD|}$

która jest po prostu długością ścieżki APQD . Niech P ₀ będzie punktem przecięcia AD i CF. Punkt ten jest powszechnie nazywany pierwszym centrum izogonicznym. Wykonaj to samo ćwiczenie z P ₀ , co z P , i znajdź punkt Q ₀ . Przez ograniczenie kątowe P ₀ leży wewnątrz △ ABC . Co więcej, △ BCF to obrót △ BDA o 60° wokół B , więc Q ₀ musi leżeć gdzieś na AD . Ponieważ ∠ CDB = 60 ° wynika z tego, że Q ₀ leży między P ₀ i D , co oznacza, że ₀₀ ​​​​AP Q re jest linią prostą, więc ${\ Displaystyle d (P_ {0} = | AD |.}$ Ponadto , jeśli ${\ Displaystyle P \ neq P_ {0}}$ , to albo P , albo Q nie będzie leżeć na AD ${\ Displaystyle d (P_ {0}) = | AD | <d (P).}$ co oznacza Teraz pozwól P wykraczać poza Δ . Od punktu powyżej istnieje ${\ Displaystyle P '\ in \ Omega}$ tak, że ${\ Displaystyle d (P ') <d (P)}$ i jak ${\ Displaystyle d (P_ {0}) \ równoważnik d (P')$ } że dla wszystkich $re ( P ) < re ( P ) {\ Displaystyle d (P_ {0}$ poza Δ . Oznacza to, że P jest ₀ Fermata Δ . Innymi słowy, Fermata to } pokrywa się z pierwszym środkiem izogonicznym .

Analiza wektorowa

Niech O, A, B, C, X będzie dowolnymi pięcioma punktami na płaszczyźnie. $, \ {\ overrightarrow {OB}}, \ {\ overrightarrow {OC}}, \ {\ overrightarrow {OX}}}$ } przez odpowiednio a , b , c , x i niech i , j , k będą wektorami jednostkowymi od O wzdłuż a , b , c .

${\ Displaystyle {\ rozpocząć {wyrównane} |\ mathbf {a} |&= \ mathbf {a \ cdot i} = (\ mathbf {a} - \ mathbf {x}) \ mathbf {\, \ cdot \, ja } +\mathbf {x\cdot i} \leq |\mathbf {a} -\mathbf {x} |+\mathbf {x\cdot i} ,\\|\mathbf {b} |&=\mathbf {b \cdot j} = (\mathbf {b} -\mathbf {x} )\mathbf {\,\cdot \,j} +\mathbf {x\cdot j} \leq |\mathbf {b} -\mathbf { x} |+\mathbf {x\cdot j} ,\\|\mathbf {c} |&=\mathbf {c\cdot k} =(\mathbf {c} -\mathbf {x} )\mathbf {\ ,\cdot \,k} +\mathbf {x\cdot k} \leq |\mathbf {c} -\mathbf {x} |+\mathbf {x\cdot k} .\end{wyrównane}}}$

Dodanie a , b , c daje

${\ Displaystyle |\ mathbf {a} |+|\ mathbf {b} |+|\ mathbf {c} |\ równoważnik |\ mathbf {a} -\ mathbf {x} |+|\ mathbf {b} -\ mathbf {x} |+|\mathbf {c} -\mathbf {x} |+x\cdot (\mathbf {i} +\mathbf {j} +\mathbf {k}).}$

Jeśli a , b , c przecinają się w punkcie O pod kątem 120°, to i + j + k = 0 , więc

${\ Displaystyle |\ mathbf {a} |+|\ mathbf {b} |+|\ mathbf {c} |\ równoważnik |\ mathbf {a} -\ mathbf {x} |+|\ mathbf {b} -\ mathbf {x} |+|\mathbf {c} -\mathbf {x} |}$

dla wszystkich x . Innymi słowy,

${\ Displaystyle | OA|+|OB|+|OC|\ równoważnik |XA|+|XB|+|XC|}$

stąd O jest punktem Fermata △ ABC .

Ten argument zawodzi, gdy trójkąt ma kąt ∠ C > 120° , ponieważ nie ma punktu O , w którym a , b , c przecinają się pod kątem 120°. Niemniej jednak można to łatwo naprawić, ponownie definiując k = − ( i + j ) i umieszczając O w C , tak aby c = 0 . Zauważ, że | k | ≤ 1 , ponieważ kąt między wektorami jednostkowymi i , j wynosi ∠ C i jest większy niż 120°. Od

${\ Displaystyle |\ mathbf {0} |\ równoważnik |\ mathbf {0} - \ mathbf {x} |+ \ mathbf {x \ cdot k},}$

trzecia nierówność nadal obowiązuje, pozostałe dwie nierówności pozostają niezmienione. Dowód jest teraz kontynuowany jak powyżej (dodając trzy nierówności i używając i + j + k = 0 ), aby dojść do tego samego wniosku, że O (lub w tym przypadku C ) musi być punktem Fermata △ ABC .

Mnożniki Lagrange'a

Innym podejściem do znalezienia punktu w trójkącie, od którego suma odległości do wierzchołków trójkąta jest minimalna, jest zastosowanie jednej z matematycznych metod optymalizacji ; w szczególności metoda mnożników Lagrange'a i twierdzenie cosinusów .

Rysujemy linie od punktu w trójkącie do jego wierzchołków i nazywamy je X , Y , Z . Niech długości tych linii będą x, y, z . Niech kąt między X i Y będzie α , Y i Z będą β . Wtedy kąt między X a Z wynosi 2π − α − β . Korzystając z metody mnożników Lagrange'a musimy znaleźć minimum Lagrange'a L , które wyraża się wzorem:

${\ Displaystyle L = x + y + z + \ lambda _ {1} (x ^ {2} + y ^ {2}-2xy\cos(\alpha )-a^{2})+\lambda _{2}(y^{2}+z^{2}-2yz\cos(\beta)-b^{2 })+\lambda _{3}(z^{2}+x^{2}-2zx\cos(\alpha +\beta )-c^{2})}$

gdzie a, b, c to długości boków trójkąta.

Zrównując każdą z pięciu pochodnych cząstkowych ${\ Displaystyle {\ tfrac {\ częściowe L} {\ częściowe x}}, { \tfrac {\częściowy L}{\częściowy y}},{\tfrac {\częściowy L}{\częściowy z}},{\tfrac {\częściowy L}{\częściowy \alpha}},{\tfrac {\ częściowe L}{\częściowe \beta }}}$ do zera i wyeliminowanie λ ₁ , λ ₂ , λ ₃ ostatecznie daje sin α = sin β i sin( α + β ) = − sin β , więc α = β = 120° . Jednak eliminacja to długa i żmudna sprawa, a wynik końcowy obejmuje tylko Przypadek 2.

Nieruchomości

Dwa izogoniczne centra to przecięcia trzech vesicae piscis , których sparowane wierzchołki są wierzchołkami trójkąta

• Gdy największy kąt trójkąta nie jest większy niż 120°, X (13) jest punktem Fermata.
• Kąty oparte na bokach trójkąta w punkcie X (13) są równe 120° (przypadek 2) lub 60°, 60°, 120° (przypadek 1).
• Okręgi opisane na trzech skonstruowanych trójkątach równobocznych są zbieżne w X ( 13).
• Współrzędne trójliniowe dla pierwszego środka izogonicznego, X (13):

${\ Displaystyle {\ rozpocząć {wyrównane} & \ csc \ lewo (A + {\ tfrac {\ pi}} {3}} \ prawej): \ csc \ lewo (B + {\ tfrac {\ pi}} {3}} \ prawo ):\csc \left(C+{\tfrac {\pi }{3}}\right)\\&=\sec \left(A-{\tfrac {\pi }{6}}\right):\sec \left(B-{\tfrac {\pi }{6}}\right):\sec \left(C-{\tfrac {\pi }{6}}\right).\end{aligned}}}$

• Trójliniowy

${\ Displaystyle {\ rozpocząć {wyrównane} & \ csc \ lewo (A- {\ tfrac {\ pi}} {3}} \ prawej): \ csc \ lewo (B- {\ tfrac {\ pi}} {3}} \right):\csc \left(C-{\tfrac {\pi }{3}}\right)\\&=\sec \left(A+{\tfrac {\pi }{6}}\right): \sec \left(B+{\tfrac {\pi }{6}}\right):\sec \left(C+{\tfrac {\pi }{6}}\right).\end{aligned}}}$

• drugiego środka izogonicznego, ( 14):

• Trójliniowy współrzędne punktu Fermata:

${\ Displaystyle 1-u + uvw \ s \ lewo (A - {\ tfrac {\ pi}} {6}} \ prawej): 1-v + uvw \ s \ lewo (B - {\ tfrac {\ pi }{6}}\right):1-w+uvw\sec \left(C-{\tfrac {\pi }{6}}\right)} gdzie odpowiednio u, v,$

w oznaczają zmienne logiczne ( A < 120°), ( B < 120°), ( C < 120°) .

• Izogonalny koniugat X (13) jest pierwszym punktem izodynamicznym , X (15):

${\ Displaystyle \ sin \ lewo (A + {\ tfrac {\ pi}} {3}} \ prawo): \ sin \ lewo (B + {\ tfrac {\ pi}} {3}} \ prawo): \ sin \ lewo ( C+{\tfrac {\pi }{3}}\right).}$

• Izogonalny koniugat X (14) jest drugim punktem izodynamicznym , X (16):

${\ Displaystyle \ sin \ lewo (A- {\ tfrac {\ pi}} {3}} \ prawej): \ sin \ lewo (B- {\ tfrac {\ pi}} {3}} \ prawej): \ sin \ lewo (C-{\tfrac {\pi }{3}}\prawo).}$

• Następujące trójkąty są równoboczne:
  • trójkąt przeciwnożny X ( 13)
  • Trójkąt przeciwnożny X (14)
  • Trójkąt pedałowy X (15)
  • Trójkąt pedałowy X (16)
  • Trójkąt cyrkulacyjny X ( 15)
  • Trójkąt cyrkulacyjny X (16)
• Proste X (13) X (15) i X (14) X (16) są równoległe do prostej Eulera . Trzy linie spotykają się w punkcie nieskończoności Eulera, X (30).
• Punkty X (13), X (14), środek okręgu opisanego i środek dziewięciu punktów leżą na okręgu Lestera .
• Linia X (13) X (14) spotyka się z linią Eulera w punkcie środkowym X (2) i X (4).
• Punkt Fermata leży w otwartym ortocentroidalnym dysku przebitym we własnym środku i może być dowolnym punktem w nim.

Skróty

Izogoniczne centra X (13) i X (14) są również znane jako odpowiednio pierwszy punkt Fermata i drugi punkt Fermata . Alternatywy to dodatni punkt Fermata i ujemny punkt Fermata . Jednak te różne nazwy mogą być mylące i być może najlepiej ich unikać. Problem polega na tym, że znaczna część literatury zaciera rozróżnienie między punktem Fermata a pierwszym punktem Fermata, podczas gdy tylko w przypadku 2 powyżej są one w rzeczywistości takie same.

Historia

To pytanie zostało zaproponowane przez Fermata jako wyzwanie dla Evangelista Torricelli . Rozwiązał problem w podobny sposób jak Fermat, chociaż zamiast tego użył przecięcia okręgów opisanych na trzech regularnych trójkątach. Jego uczeń, Viviani, opublikował rozwiązanie w 1659 roku.

Zobacz też

• Mediana geometryczna lub punkt Fermata – Webera, punkt minimalizujący sumę odległości do więcej niż trzech podanych punktów.
• Twierdzenie Lestera
• Centrum trójkąta
• Punkty Napoleona
• Problem Webera

Linki zewnętrzne

• „Problem Fermata-Torricellego” , Encyklopedia matematyki , EMS Press , 2001 [1994]
• Fermat Point autorstwa Chrisa Bouchera, The Wolfram Demonstrations Project .
• Uogólnienie Fermata-Torricellego w szkicach dynamicznej geometrii Interaktywny szkic uogólnia punkt Fermata-Torricellego.
• Praktyczny przykład punktu Fermata
• iOS Interaktywny szkic