Stabilność Układu Słonecznego

Stabilność Układu Słonecznego jest przedmiotem wielu badań w astronomii . Chociaż planety były stabilne, gdy były obserwowane historycznie, i będą w perspektywie krótkoterminowej, ich słaby wpływ grawitacyjny na siebie może sumować się w nieprzewidywalny sposób.

Z tego powodu (między innymi) Układ Słoneczny jest chaotyczny w technicznym sensie matematycznej teorii chaosu i nawet najbardziej precyzyjne długoterminowe modele ruchu orbitalnego Układu Słonecznego nie są ważne przez więcej niż kilkadziesiąt milionów lat.

Układ Słoneczny jest stabilny w kategoriach ludzkich i znacznie dalej, biorąc pod uwagę, że jest mało prawdopodobne, aby którakolwiek z planet zderzyła się ze sobą lub została wyrzucona z układu w ciągu następnych kilku miliardów lat, a orbita Ziemi będzie względnie stabilna .

Od prawa grawitacji Newtona (1687) matematycy i astronomowie (tacy jak Pierre-Simon Laplace , Joseph Louis Lagrange , Carl Friedrich Gauss , Henri Poincaré , Andrey Kolmogorov , Vladimir Arnold i Jürgen Moser ) szukali dowodów na stabilność ruchy planet, a poszukiwanie to doprowadziło do wielu odkryć matematycznych i kilku kolejnych „dowodów” stabilności Układu Słonecznego.

Przegląd i wyzwania

Główny artykuł: problem n-ciał

Orbity planet są otwarte na długoterminowe zmiany. Modelowanie Układu Słonecznego jest przypadkiem fizyki n -ciał , który jest generalnie nierozwiązywalny, chyba że za pomocą symulacji numerycznej.

Rezonans

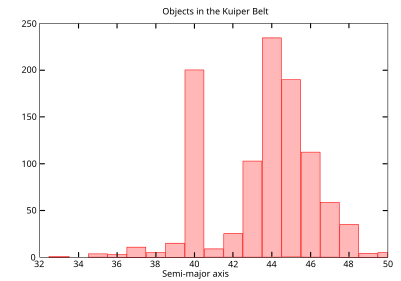
Wykres przedstawiający liczbę obiektów pasa Kuipera dla danej odległości (w jednostkach astronomicznych , tj. odległości od Słońca do Ziemi) od Słońca

Rezonans orbitalny ma miejsce, gdy dowolne dwa okresy mają prosty stosunek liczbowy. Najbardziej podstawowym okresem dla obiektu w Układzie Słonecznym jest jego okres orbitalny , a rezonanse orbitalne przenikają Układ Słoneczny. W 1867 roku amerykański astronom Daniel Kirkwood zauważył, że asteroidy w pasie planetoid nie są rozmieszczone przypadkowo. W pasie były wyraźne przerwy w miejscach, które odpowiadały rezonansom z Jowiszem . Na przykład nie było asteroid przy rezonansie 3: 1 - w odległości 2,5 AU (370 milionów km; 230 milionów mil) - lub przy rezonansie 2: 1 przy 3,3 AU (490 milionów km; 310 milionów mil). Są one obecnie znane jako luki Kirkwooda . Później odkryto, że niektóre asteroidy krążą w tych szczelinach, ale ich orbity są niestabilne i ostatecznie wyrwą się z rezonansu z powodu bliskich spotkań z dużą planetą.

Inną powszechną formą rezonansu w Układzie Słonecznym jest rezonans wirowo-orbitalny, w którym okres obrotu (czas, w którym planeta lub księżyc obraca się raz wokół własnej osi) ma prosty związek liczbowy z okresem orbity. Przykładem jest Księżyc , który znajduje się w rezonansie wirowo-orbitalnym 1:1, który utrzymuje jego drugą stronę z dala od Ziemi. (Ta cecha jest również znana jako „ blokowanie pływów ”). Innym przykładem jest Merkury , który znajduje się w rezonansie spinowo-orbitalnym 3: 2 ze Słońcem.

Przewidywalność

Orbity planet są chaotyczne w dłuższych skalach czasowych, w taki sposób, że cały Układ Słoneczny ma czas Lapunowa w zakresie 2–230 milionów lat. We wszystkich przypadkach oznacza to, że położenie planety wzdłuż jej orbity ostatecznie staje się niemożliwe do przewidzenia z jakąkolwiek pewnością. W niektórych przypadkach same orbity mogą się radykalnie zmienić. Taki chaos przejawia się najsilniej w zmianach ekscentryczności , przy czym orbity niektórych planet stają się znacznie bardziej – lub mniej – eliptyczne .

W obliczeniach niewiadome obejmują asteroidy , moment kwadrupolowy Słońca , utratę masy przez Słońce przez promieniowanie i wiatr słoneczny , opór wiatru słonecznego na planetarne magnetosfery , galaktyczne siły pływowe i skutki przelatujących gwiazd .

Scenariusze

Rezonans Neptuna – Plutona

Neptun – Pluton znajduje się w rezonansie orbitalnym 3 : 2 . CJ Cohen i EC Hubbard z Naval Surface Warfare Center Dahlgren Division odkryli to w 1965 roku. Chociaż sam rezonans pozostanie stabilny w krótkim okresie, niemożliwe staje się przewidzenie pozycji Plutona z jakimkolwiek stopniem dokładności, ponieważ niepewność w pozycja rośnie o współczynnik e z każdym czasem Lapunowa , co dla Plutona jest 10-20 milionów lat w przyszłość. Tak więc w skali czasu setek milionów lat faza orbitalna Plutona staje się niemożliwa do określenia, nawet jeśli orbita Plutona wydaje się być idealnie stabilna w skali czasu 10 MYR ( Ito i Tanikawa 2002, MNRAS).

Rezonans peryhelium-precesji Merkurego – Jowisza 1: 1

Planeta Merkury jest szczególnie podatna na wpływy Jowisza z powodu niewielkiego niebiańskiego zbiegu okoliczności: peryhelium Merkurego , punkt, w którym Merkury zbliża się do Słońca, precesuje z prędkością około 1,5 stopnia na 1000 lat, a peryhelium Jowisza precezuje tylko nieznacznie wolniej. W pewnym momencie te dwa elementy mogą zsynchronizować się, w którym to czasie ciągłe przyciąganie grawitacyjne Jowisza mogłoby się kumulować i zepchnąć Merkurego z kursu z prawdopodobieństwem 1–2%, za 3–4 miliardy lat w przyszłość. Może to całkowicie wyrzucić go z Układu Słonecznego lub wysłać na kurs kolizyjny z Wenus , Słońce lub Ziemia.

Tempo precesji peryhelium Merkurego jest zdominowane przez interakcje planeta-planeta, ale około 7,5% tempa precesji peryhelium Merkurego pochodzi z efektów opisanych przez ogólną teorię względności . Praca Laskar i Gastineau (opisana poniżej) pokazała znaczenie ogólnej teorii względności dla długoterminowej stabilności Układu Słonecznego. W szczególności bez GR wskaźnik niestabilności Merkurego byłby 60 razy wyższy niż w przypadku GR. Modelując czas niestabilności Merkurego jako jednowymiarowy proces dyfuzji Fokkera-Plancka , można zbadać statystycznie zależność między czasem niestabilności Merkurego a rezonansem peryhelium-precesji Merkurego-Jowisza 1: 1. Ten model dyfuzji pokazuje, że GR nie tylko oddala Merkurego i Jowisza od wpadnięcia w rezonans 1:1, ale także zmniejsza szybkość, z jaką Merkury dyfunduje przez przestrzeń fazowa . W ten sposób GR nie tylko zmniejsza prawdopodobieństwo niestabilności Merkurego, ale także wydłuża czas, w którym prawdopodobnie nastąpi.

Galileuszowy rezonans księżyca

Galileuszowe księżyce Jowisza doświadczają silnego rozpraszania pływów i wzajemnych interakcji ze względu na ich rozmiar i bliskość Jowisza. Obecnie Io , Europa i Ganimedes są ze sobą w rezonansie Laplace'a 4:2:1 , a każdy księżyc wykonuje dwie orbity na każdą orbitę następnego. Za około 1,5 miliarda lat migracja tych księżyców na zewnątrz uwięzi czwarty i najbardziej oddalony księżyc, Callisto , w kolejny rezonans 2:1 z Ganimedesem. Ten rezonans 8:4:2:1 spowoduje migrację Callisto na zewnątrz i może pozostać stabilny z około 56% prawdopodobieństwem lub zostać zakłócony, gdy Io zwykle opuszcza łańcuch.

Chaos z procesów geologicznych

osiowe nachylenie Ziemi , które z powodu tarcia w płaszczu Ziemi w wyniku interakcji pływów z Księżycem stanie się chaotyczne za 1,5 do 4,5 miliarda lat.

Zobacz także: Hipoteza kataklizmowego przesunięcia biegunów

Wpływy zewnętrzne

Obiekty pochodzące spoza Układu Słonecznego również mogą na niego wpływać. Chociaż technicznie rzecz biorąc, nie są one częścią Układu Słonecznego w celu badania jego wewnętrznej stabilności, mogą go jednak zmienić. Niestety, przewidywanie potencjalnego wpływu tych obiektów pozasłonecznych jest jeszcze trudniejsze niż przewidywanie wpływu obiektów w systemie po prostu ze względu na same odległości. Wśród znanych obiektów, które mogą znacząco wpłynąć na Układ Słoneczny, jest gwiazda Gliese 710 , który ma przejść w pobliżu układu za około 1,281 miliona lat. Chociaż nie oczekuje się, że gwiazda znacząco wpłynie na orbity głównych planet, może znacznie zakłócić obłok Oorta , potencjalnie powodując dużą aktywność komet w całym Układzie Słonecznym. Istnieje co najmniej tuzin innych gwiazd, które mogą zbliżyć się do siebie w ciągu najbliższych kilku milionów lat. W 2022 roku Garett Brown i Hanno Rein z University of Toronto opublikował badanie badające długoterminową stabilność Układu Słonecznego w obecności słabych perturbacji spowodowanych przelotami gwiazd. Ustalili, że gdyby przechodząca gwiazda zmieniła półoś wielką Neptuna o co najmniej 0,03 AU (4,49 miliona km; 2,79 miliona mil) , zwiększyłoby to ryzyko niestabilności 10-krotnie w ciągu kolejnych 5 miliardów lat. Oszacowali również, że przelot o tej wielkości prawdopodobnie nie nastąpi przez 100 miliardów lat.

Studia

LONGSTOP

Projekt LONGSTOP (Long-term Gravitational Study of the Outer Planets) był międzynarodowym konsorcjum zajmującym się dynamiką Układu Słonecznego, kierowanym przez Archiego Roya w 1982 roku . Polegało to na stworzeniu modelu na superkomputerze, integrującego orbity (tylko) planet zewnętrznych. Jego wyniki ujawniły kilka dziwnych wymian energii między planetami zewnętrznymi, ale żadnych oznak poważnej niestabilności.

Cyfrowy ogródek

Inny projekt polegał na zbudowaniu Cyfrowego Orrery przez Gerry'ego Sussmana i jego grupę z MIT w 1988 roku. Grupa wykorzystała superkomputer do zintegrowania orbit planet zewnętrznych na przestrzeni 845 milionów lat (około 20 procent wieku Układu Słonecznego). W 1988 roku Sussman i Wisdom znaleźli dane za pomocą Orrery, które ujawniły, że orbita Plutona wykazuje oznaki chaosu, częściowo z powodu jego szczególnego rezonansu z Neptunem .

Jeśli orbita Plutona jest chaotyczna, to technicznie cały Układ Słoneczny jest chaotyczny, ponieważ każde ciało, nawet tak małe jak Pluton, w pewnym stopniu wpływa na inne poprzez oddziaływania grawitacyjne.

Laskar 1

W 1989 roku Jacques Laskar z Bureau des Longitudes w Paryżu opublikował wyniki swojej numerycznej integracji Układu Słonecznego na przestrzeni 200 milionów lat. Nie były to pełne równania ruchu, ale raczej uśrednione równania na wzór tych, których użył Laplace . Praca Laskara wykazała, że ​​orbita Ziemi (podobnie jak orbity wszystkich planet wewnętrznych) jest chaotyczna i błąd wynoszący zaledwie 15 metrów w pomiarze dzisiejszego położenia Ziemi uniemożliwiłby przewidzenie, w którym miejscu Ziemi będzie się znajdowała. swoją orbitę za nieco ponad 100 milionów lat.

Laskar i Gastineau

Jacques Laskar i jego kolega Mickaël Gastineau w 2008 roku przyjęli dokładniejsze podejście, bezpośrednio symulując 2501 możliwych przyszłości. Każdy z 2501 przypadków ma nieco inne warunki początkowe: pozycja Merkurego zmienia się o około 1 metr (3,3 stopy ) między jedną symulacją a następną. W 20 przypadkach Merkury wchodzi na niebezpieczną orbitę i często kończy się kolizją z Wenus lub zanurzeniem w Słońcu. Poruszając się po tak zakrzywionej orbicie, grawitacja Merkurego z większym prawdopodobieństwem wytrąci inne planety z ich ustalonych ścieżek: w jednym symulowanym przypadku perturbacje Merkurego wysłały Marsa kierując się w stronę Ziemi.

Batygina i Laughlina

Niezależnie od Laskara i Gastineau, Batygin i Laughlin również bezpośrednio symulowali Układ Słoneczny 20 miliardów lat w przyszłość. Ich wyniki osiągnęły te same podstawowe wnioski, co Laskar i Gastineau, jednocześnie zapewniając dolną granicę miliarda lat dynamicznej długości życia Układu Słonecznego.

Browna i Reina

W 2020 roku Garett Brown i Hanno Rein z University of Toronto opublikowali wyniki numerycznej integracji Układu Słonecznego na przestrzeni 5 miliardów lat. Ich praca wykazała, że ​​orbita Merkurego jest bardzo chaotyczna i że błąd tak mały, jak 0,38 milimetra (0,015 cala ) w pomiarze dzisiejszej pozycji Merkurego uniemożliwiłby przewidzenie ekscentryczności jego orbity za nieco ponad 200 milionów lat.

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Stability_of_the_Solar_System&oldid=1144414907 ”