Jednostka astronomiczna

Ten artykuł dotyczy jednostki długości. Aby uzyskać informacje na temat stałych, zobacz stała astronomiczna . Aby zapoznać się z jednostkami astronomicznymi, zobacz astronomiczny system jednostek .

Jednostka astronomiczna
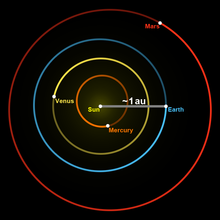Astronomical unit.png
Szara linia wskazuje odległość Ziemia–Słońce, która wynosi średnio około 1 jednostki astronomicznej.
Informacje ogólne
System jednostkowy
Astronomiczny układ jednostek (dopuszczony do użytku z układem SI)
Jednostką długość
Symbol au lub AU lub AU
Konwersje
1 au lub AU lub AU w ... ... jest równe ...
    jednostki metryczne ( SI ).      1.495 978 707 × 10 11 m
    jednostki imperialne i amerykańskie      9,2956 × 10 7 mil
   jednostki astronomiczne     _   4,8481 × 10-6 szt . 1,5813 × 10-5 li  
   

Jednostka astronomiczna (symbol: au lub AU lub AU ) jest jednostką długości , mniej więcej odległości od Ziemi do Słońca iw przybliżeniu równą 150 milionom kilometrów (93 milionów mil) lub 8,3 minutom świetlnym. Rzeczywista odległość od Ziemi do Słońca zmienia się o około 3%, gdy Ziemia okrąża Słońce, od maksimum ( aphelium ) do minimum ( peryhelium ) iz powrotem raz w roku. Jednostka astronomiczna została pierwotnie pomyślana jako średnia aphelium i peryhelium Ziemi; jednak od 2012 roku został zdefiniowany jako dokładnie 149 597 870 700 m (patrz poniżej kilka przeliczeń).

Jednostka astronomiczna jest używana głównie do mierzenia odległości w Układzie Słonecznym lub wokół innych gwiazd. Jest to również podstawowy składnik definicji innej jednostki długości astronomicznej, parseka .

Historia użycia symboli

Dla jednostek astronomicznych używano różnych symboli jednostek i skrótów. W rezolucji z 1976 roku Międzynarodowa Unia Astronomiczna (IAU) użyła symbolu A do oznaczenia długości równej jednostce astronomicznej. W literaturze astronomicznej symbol AU był (i pozostaje) powszechny. W 2006 roku Międzynarodowe Biuro Miar i Wag (BIPM) zaleciło ua jako symbol jednostki. W nienormatywnym Załączniku C do ISO 80000-3 :2006 (obecnie wycofanym) symbolem jednostki astronomicznej było „ua”.

W 2012 roku IAU, zwracając uwagę, że „obecnie używane są różne symbole jednostek astronomicznych”, zaleciła użycie symbolu „au”. Czasopisma naukowe publikowane przez Amerykańskie Towarzystwo Astronomiczne i Królewskie Towarzystwo Astronomiczne przyjęły następnie ten symbol. W rewizji broszury SI z 2014 i 2019 roku BIPM użył symbolu jednostki „au”. Norma ISO 80000-3:2019, która zastępuje normę ISO 80000-3:2006, nie wspomina o jednostce astronomicznej.

Opracowanie definicji jednostek

Zobacz też: orbita Ziemi

Orbita Ziemi wokół Słońca jest elipsą . Półoś wielka tej eliptycznej orbity jest zdefiniowana jako połowa prostego odcinka , który łączy peryhelium i aphelium . Środek Słońca leży na tym odcinku linii prostej, ale nie w jego punkcie środkowym. Ponieważ elipsy są dobrze rozumianymi kształtami, mierzenie punktów ich skrajności zdefiniowało matematycznie dokładny kształt i umożliwiło obliczenia dla całej orbity, a także przewidywania oparte na obserwacjach. Ponadto dokładnie wyznaczył największą odległość w linii prostej, jaką Ziemia pokonuje w ciągu roku, określając czasy i miejsca obserwacji największej paralaksy (pozorne przesunięcia pozycji) w pobliskich gwiazdach. Znajomość przesunięcia Ziemi i przesunięcia gwiazdy umożliwiła obliczenie odległości gwiazdy. Ale wszystkie pomiary są obarczone pewnym stopniem błędu lub niepewności, a niepewność co do długości jednostki astronomicznej tylko zwiększa niepewność co do odległości gwiazd. Poprawa precyzji zawsze była kluczem do lepszego zrozumienia astronomii. dokładnych obserwacji efektów opisanych przez teorię względności Einsteina oraz od używanych przez nią narzędzi matematycznych.

Ulepszone pomiary były nieustannie sprawdzane i sprawdzane krzyżowo dzięki lepszemu zrozumieniu praw mechaniki nieba , które rządzą ruchami obiektów w przestrzeni. Oczekiwane pozycje i odległości obiektów w ustalonym czasie są obliczane (w au) na podstawie tych praw i łączone w zbiór danych zwany efemerydą . NASA Jet Propulsion Laboratory HORIZONS System zapewnia jedną z kilku usług obliczeniowych efemeryd.

W 1976 roku, aby ustalić jeszcze precyzyjną miarę jednostki astronomicznej, IAU formalnie przyjęła nową definicję . Chociaż bezpośrednio opierała się na najlepszych wówczas dostępnych pomiarach obserwacyjnych, definicja została przekształcona pod kątem najlepszych wówczas matematycznych wyprowadzeń z mechaniki nieba i efemeryd planetarnych. Stwierdzono, że „astronomiczną jednostką długości jest ta długość ( A ), dla której stała grawitacyjna Gaussa ( k ) przyjmuje wartość 0,017 202 098 95 , gdy jednostkami miary są astronomiczne jednostki długości, masy i czasu”. Równoważnie, zgodnie z tą definicją, jeden au to „promień niezaburzonej kołowej orbity Newtona wokół Słońca cząstki o nieskończenie małej masie, poruszającej się z częstotliwością kątową 0,017 202 098 95 radianów dziennie ” ; lub alternatywnie długość, dla której heliocentryczna stała grawitacyjna (iloczyn G M ☉ ) jest równa ( 0,017 202 098 95 ) 2 au 3 /d 2 , gdy długość jest używana do opisu położenia obiektów w Układzie Słonecznym.

Późniejsze eksploracje Układu Słonecznego przez sondy kosmiczne umożliwiły precyzyjne pomiary względnych położeń planet wewnętrznych i innych obiektów za pomocą radaru i telemetrii . Podobnie jak w przypadku wszystkich pomiarów radarowych, polegają one na pomiarze czasu potrzebnego do fotonów od obiektu. Ponieważ wszystkie fotony poruszają się z prędkością światła w próżni, która jest podstawową stałą wszechświata, odległość obiektu od sondy jest obliczana jako iloczyn prędkości światła i zmierzonego czasu. Jednak ze względu na precyzję obliczenia wymagają dostosowania do takich rzeczy, jak ruchy sondy i obiektu podczas tranzytu fotonów. Ponadto sam pomiar czasu musi zostać przełożony na standardową skalę, która uwzględnia relatywistyczną dylatację czasu. Porównanie pozycji efemeryd z pomiarami czasu wyrażonymi w barycentrycznym czasie dynamicznym (TDB) prowadzi do wartości prędkości światła w jednostkach astronomicznych na dzień ( 86 400 s ). Do 2009 roku IAU zaktualizowała swoje standardowe miary, aby odzwierciedlić ulepszenia, i obliczyła prędkość światła na 173,144 632 6847 (69) au / d (TDB).

00 W 1983 roku CIPM zmodyfikował Międzynarodowy Układ Jednostek Miar (SI), aby metr był zdefiniowany jako odległość przebyta przez światło w próżni w ciągu 1/299 792 458 sekundy . Zastąpiło to poprzednią definicję, obowiązującą w latach 1960-1983, zgodnie z którą miernik był równy określonej liczbie długości fal określonej linii emisyjnej kryptonu-86. (Powodem zmiany była ulepszona metoda pomiaru prędkości światła). Prędkość światła można było wówczas wyrazić dokładnie jako c = 299 792 458 m/s , standard przyjęty również przez standardy numeryczne IERS . Z tej definicji i standardu IAU z 2009 r. wynika, że ​​czas przejścia światła przez jednostkę astronomiczną wynosi τ A = 499,004 783 8061 ± 0,000 000 01 s , czyli nieco ponad 8 minut i 19 sekund. Mnożąc, najlepsze oszacowanie IAU 2009 wyniosło A = c τ A = 149 597 870 700 ± 3 m , na podstawie porównania Jet Propulsion Laboratory i efemeryd IAA-RAS .

W 2006 roku BIPM podał wartość jednostki astronomicznej jako 1,495 978 706 91 (6) × 10 11 m . W rewizji broszury SI z 2014 r. BIPM uznał redefinicję jednostki astronomicznej przez IAU z 2012 r. Jako 149 597 870 700 m .

Oszacowanie to nadal pochodziło z obserwacji i pomiarów obarczonych błędem i opierało się na technikach, które nie ustandaryzowały jeszcze wszystkich efektów relatywistycznych, a zatem nie były stałe dla wszystkich obserwatorów. W 2012 roku, stwierdzając, że samo wyrównanie teorii względności uczyniłoby definicję zbyt złożoną, IAU po prostu wykorzystała szacunki z 2009 roku, aby przedefiniować jednostkę astronomiczną jako konwencjonalną jednostkę długości bezpośrednio powiązaną z metrem (dokładnie 149 597 870 700 m ) . Nowa definicja uznaje również w konsekwencji, że jednostka astronomiczna ma teraz odgrywać rolę o mniejszym znaczeniu, ograniczoną w użyciu do wygody w niektórych zastosowaniach.

1 jednostka astronomiczna = 149 597 870 700 metrów (z definicji)
= 149 597 870,700 kilometrów dokładnie)
( ≈ 4,848 136 8111 × 10-6 parseków
≈ ≈ 1,581 250 740 98 × 10-5 lat świetlnych
92 955 807,273 mil ≈
499,004 783 84 sekund świetlnych
≈ 8,316 746 3973 minut świetlnych

Ta definicja sprawia, że ​​prędkość światła, zdefiniowana jako dokładnie 299 792 458 m/s , równa się dokładnie 299 792 458 × 86 400 ÷ 149 597 870 700 , czyli około 173,144 632 674 240 au/d, czyli około 60 części na bilion mniej niż Szacunek z 2009 r.

Użycie i znaczenie

W definicjach stosowanych przed 2012 rokiem jednostka astronomiczna była zależna od heliocentrycznej stałej grawitacyjnej , czyli iloczynu stałej grawitacyjnej G i masy Słońca M ☉ . Ani G , ani M ☉ nie mogą być zmierzone z dużą dokładnością oddzielnie, ale wartość ich iloczynu jest znana bardzo dokładnie z obserwacji względnych położeń planet ( trzecie prawo Keplera wyrażone w kategoriach grawitacji Newtona). Tylko iloczyn jest wymagany do obliczenia pozycji planet dla efemeryd, więc efemerydy są obliczane w jednostkach astronomicznych, a nie w jednostkach SI.

Obliczenie efemeryd wymaga również rozważenia skutków ogólnej teorii względności . W szczególności odstępy czasowe mierzone na powierzchni Ziemi ( czas ziemski , TT) nie są stałe w porównaniu z ruchami planet: sekunda ziemska (TT) wydaje się być dłuższa w okolicach stycznia i krótsza w okolicach lipca w porównaniu z „sekundą planetarną” " (konwencjonalnie mierzone w TDB). Dzieje się tak, ponieważ odległość między Ziemią a Słońcem nie jest stała (waha się między 0,983 289 8912 a 1,016 710 3335 au ), a gdy Ziemia znajduje się bliżej Słońca ( peryhelium ), pole grawitacyjne Słońca jest silniejsze, a Ziemia porusza się szybciej wzdłuż swojej orbitalnej ścieżki. Ponieważ metr jest zdefiniowany w sekundach, a prędkość światła jest stała dla wszystkich obserwatorów, metr ziemski wydaje się okresowo zmieniać długość w porównaniu z „metrem planetarnym”.

Metr jest definiowany jako jednostka odpowiedniej długości , ale definicja SI nie określa tensora metrycznego , który ma być używany do jej określania. Rzeczywiście, Międzynarodowy Komitet Miar i Wag (CIPM) zauważa, że ​​„jego definicja ma zastosowanie tylko w zakresie przestrzennym na tyle małym, że skutki niejednorodności pola grawitacyjnego można zignorować”. W związku z tym miernik jest niezdefiniowany do celów pomiaru odległości w Układzie Słonecznym. Definicja jednostki astronomicznej z 1976 roku była niekompletna, ponieważ nie określała układu odniesienia , w którym należy mierzyć czas, ale okazała się praktyczna do obliczania efemeryd: zaproponowano pełniejszą definicję, zgodną z ogólną teorią względności, i „energiczny debata” trwała do sierpnia 2012 roku, kiedy IAU przyjęła obecną definicję 1 jednostki astronomicznej = 149 597 870 700 metrów .

Jednostka astronomiczna jest zwykle używana do określania odległości w skali systemu gwiezdnego , takich jak rozmiar dysku protogwiazdy lub odległość heliocentryczna asteroidy, podczas gdy inne jednostki są używane w astronomii do określania innych odległości . Jednostka astronomiczna jest zbyt mała, aby była wygodna dla odległości międzygwiezdnych, gdzie powszechnie stosuje się parsek i rok świetlny . Parsek ( sekunda łuku paralaksy ) jest definiowany w jednostkach astronomicznych, będących odległością obiektu z paralaksą 1″ . Rok świetlny jest często używany w popularnych pracach, ale nie jest zatwierdzoną jednostką spoza układu SI i jest rzadko używany przez zawodowych astronomów.

Podczas symulacji numerycznego modelu Układu Słonecznego jednostka astronomiczna zapewnia odpowiednią skalę, która minimalizuje błędy ( przepełnienie , niedopełnienie i obcięcie ) w obliczeniach zmiennoprzecinkowych .

Historia

Książka O rozmiarach i odległościach Słońca i Księżyca , przypisywana Arystarchowi , podaje, że odległość do Słońca jest 18 do 20 razy większa od odległości do Księżyca , podczas gdy rzeczywisty stosunek wynosi około 389,174 . To ostatnie oszacowanie oparto na kącie między półksiężycem a Słońcem, który oszacował na 87 ° (prawdziwa wartość jest bliska 89,853 ° ). W zależności od odległości, jaką van Helden zakłada, że ​​Arystarch użył odległości do Księżyca, obliczona przez niego odległość do Słońca mieściłaby się w przedziale od 380 do 1520 promieni Ziemi.

Według Euzebiusza w Praeparatio evangelica (Księga XV, rozdział 53), Eratostenes określił odległość do Słońca jako „σταδιων μυριαδας τετρακοσιας και οκτωκισμυριας” (dosłownie „miriadów stadionów 400 i 80 000 ″ ), ale z dodatkową uwagą, że w w tekście greckim zgodność gramatyczna zachodzi między miriadami (nie stadionami ) z jednej strony a zarówno 400 , jak i 80 000 z drugiej, ponieważ w języku greckim, w przeciwieństwie do angielskiego, wszystkie trzy (lub wszystkie cztery, jeśli jeden miałby obejmować stadiony ) są odmieniane Zostało to przetłumaczone jako 4 080 000 stadionów (przekład Edwina Hamiltona Gifforda z 1903 r. ) Lub jako 804 000 000 stadionów (wydanie Édourad des Places [ de ] , datowane na lata 1974–1991). metrów, pierwsze tłumaczenie daje od 754 800 km do 775 200 km , czyli o wiele za mało, podczas gdy drugie tłumaczenie podaje od 148,7 do 152,8 miliona kilometrów (z dokładnością do 2%). Hipparch podał również szacunkową odległość Ziemi od Słońce, cytowane przez Pappusa jako równe 490 promieniom Ziemi. Zgodnie z domniemanymi rekonstrukcjami Noela Swerdlowa i GJ Toomera , wynikało to z jego założenia „najmniej dostrzegalnej” paralaksy słonecznej wynoszącej 7 ′ .

Chiński traktat matematyczny, Zhoubi Suanjing (ok. I wpne), pokazuje, jak odległość do Słońca można obliczyć geometrycznie, wykorzystując różne długości cieni w południe obserwowanych w trzech miejscach oddalonych od siebie o 1000 li oraz założenie, że Ziemia jest płaska .


Odległość do Słońca oszacowana przez 		Oszacować w au
Paralaksa słoneczna
promienie ziemi

Arystarch (III wiek p.n.e.) (w On Sizes )    		13′ 24″ – 7′ 12″ 256,5 – 477,8 0,011 – 0,020

Archimedes (III wiek pne) (w The Sand Reckoner ) 		21″ 10 000 0,426
Hipparch (II wiek p.n.e.) 7′ 490 0,021

Posidonius (I wpne) (cytowany przez rówieśnika Cleomedesa ) 		21″ 10 000 0,426
Ptolemeusz (II wiek) 2′ 50″ 1210 0,052
Godefroy Wendelin (1635) 15″ 14 000 0,597
Jeremiasz Horrocks (1639) 15″ 14 000 0,597
Christiaan Huygens (1659) 8,2″ 25 086 1.068
Cassini i bogatszy (1672) 9,5″ 21 700 0,925
Flamsteed (1672) 9,5″ 21 700 0,925
Jérôme Lalande (1771) 8,6″ 24 000 1.023
Szymon Newcomb (1895) 8,80″ 23 440 0,9994
Arthur Hinks (1909) 8,807″ 23 420 0,9985
H.Spencer Jones (1941) 8,790″ 23 466 1.0005
współczesna astronomia 8.794 143 ″ 23 455 1.0000

W II wieku n.e. Ptolemeusz oszacował średnią odległość Słońca na 1210 promieni Ziemi . Aby określić tę wartość, Ptolemeusz zaczął od pomiaru paralaksy Księżyca, znajdując poziomą paralaksę księżycową 1 ° 26 ′, która była o wiele za duża. promienia Następnie 64 + 1/6 wyprowadził maksymalną odległość księżycową równą Ziemi. Ze względu na usunięcie błędów w jego figurze paralaksy, jego teorii orbity Księżyca i innych czynników, figura ta była w przybliżeniu poprawna. Następnie zmierzył pozorne rozmiary Słońca i Księżyca i doszedł do wniosku, że pozorna średnica Słońca była równa pozornej średnicy Księżyca w największej odległości Księżyca, a na podstawie zapisów zaćmień Księżyca oszacował tę pozorną średnicę jako a także pozorna średnica stożka cienia Ziemi, przez który przechodzi Księżyc podczas zaćmienia Księżyca. Biorąc pod uwagę te dane, odległość Słońca od Ziemi można obliczyć trygonometrycznie na 1210 promieni Ziemi. Daje to stosunek odległości Słońca do Księżyca wynoszący około 19, co odpowiada figurze Arystarcha. Chociaż procedura Ptolemeusza jest teoretycznie wykonalna, jest bardzo wrażliwa na niewielkie zmiany danych, do tego stopnia, że ​​zmiana pomiaru o kilka procent może sprawić, że odległość słoneczna będzie nieskończona.

Po przekazaniu astronomii greckiej do średniowiecznego świata islamu astronomowie dokonali pewnych zmian w modelu kosmologicznym Ptolemeusza, ale nie zmienili zbytnio jego oszacowania odległości Ziemia-Słońce. Na przykład we wstępie do astronomii ptolemejskiej al-Farghānī podał średnią odległość słoneczną równą 1170 promieni Ziemi, podczas gdy w swoim zij al-Battānī zastosował średnią odległość słoneczną równą 1108 promieni Ziemi. Późniejsi astronomowie, tacy jak al-Bīrūnī , używali podobnych wartości. Później w Europie Kopernik i Tycho Brahe również używali porównywalnych liczb ( 1142 i 1150 promieni Ziemi), więc przybliżona odległość Ziemia-Słońce Ptolemeusza przetrwała do XVI wieku.

Johannes Kepler jako pierwszy zdał sobie sprawę, że szacunki Ptolemeusza muszą być znacznie za niskie (według Keplera przynajmniej trzykrotnie) w swoich tablicach rudolfińskich (1627). Prawa ruchu planet Keplera umożliwiły astronomom obliczenie względnych odległości planet od Słońca i ponownie rozbudziły zainteresowanie pomiarem wartości bezwzględnej dla Ziemi (którą można by następnie zastosować do innych planet). Wynalezienie teleskopu umożliwiło znacznie dokładniejsze pomiary kątów niż jest to możliwe gołym okiem. Flamandzki astronom Godefroy Wendelin powtórzył pomiary Arystarcha w 1635 roku i stwierdził, że wartość Ptolemeusza była co najmniej jedenastokrotnie za niska.

Nieco dokładniejsze oszacowanie można uzyskać obserwując tranzyt Wenus . Mierząc tranzyt w dwóch różnych miejscach, można dokładnie obliczyć paralaksę Wenus, a ze względnej odległości Ziemi i Wenus od Słońca paralaksę słoneczną α (której nie można zmierzyć bezpośrednio ze względu na jasność Słońca). Jeremiah Horrocks próbował oszacować na podstawie swoich obserwacji tranzytu z 1639 r. (Opublikowanych w 1662 r.), Podając paralaksę słoneczną 15 ″ , podobną do figury Wendelina. Paralaksa słoneczna jest związana z odległością Ziemia-Słońce mierzoną w promieniach Ziemi przez

Im mniejsza paralaksa słoneczna, tym większa odległość między Słońcem a Ziemią: paralaksa słoneczna 15 ″ odpowiada odległości Ziemia-Słońce wynoszącej 13 750 promieni Ziemi.

Christiaan Huygens uważał, że odległość była jeszcze większa: porównując pozorne rozmiary Wenus i Marsa , oszacował wartość na około 24 000 promieni Ziemi, co odpowiada paralaksie słonecznej 8,6″ . Chociaż szacunki Huygensa są niezwykle bliskie współczesnym wartościom, historycy astronomii często je odrzucają z powodu wielu nieudowodnionych (i błędnych) założeń, które musiał przyjąć, aby jego metoda zadziałała; dokładność jego wartości wydaje się opierać bardziej na szczęściu niż na dobrym pomiarze, a jego różne błędy wzajemnie się znoszą.

Tranzyty Wenus przez tarczę Słońca były przez długi czas najlepszą metodą pomiaru jednostki astronomicznej, pomimo trudności (tutaj tzw. „efekt czarnej kropli”) i rzadkości obserwacji.

Jean Richer i Giovanni Domenico Cassini zmierzyli paralaksę Marsa między Paryżem a Cayenne w Gujanie Francuskiej , kiedy Mars znajdował się najbliżej Ziemi w 1672 roku. Uzyskali wartość paralaksy słonecznej 9,5 cala , co odpowiada odległości Ziemia-Słońce wynoszącej około 22 000 promieni Ziemi. Byli także pierwszymi astronomami, którzy mieli dostęp do dokładnej i wiarygodnej wartości promienia Ziemi, który ich kolega Jean Picard zmierzył w 1669 roku jako 3 269 000 toisów . W tym samym roku nastąpiło kolejne oszacowanie jednostki astronomicznej przez Johna Flamsteeda , który dokonał tego samodzielnie, mierząc marsjańską paralaksę dzienną . Inny kolega, Ole Rømer , odkrył skończoną prędkość światła w 1676 r.: prędkość była tak duża, że ​​zwykle określano ją jako czas potrzebny światłu na podróż ze Słońca na Ziemię lub „czas świetlny na jednostkę odległości”, a konwencja, której przestrzegają astronomowie do dziś.

Lepszą metodę obserwacji tranzytów Wenus opracował James Gregory i opublikował w jego Optica Promata (1663). Był zdecydowanie popierany przez Edmonda Halleya i został zastosowany do tranzytów Wenus obserwowanych w 1761 i 1769, a następnie ponownie w 1874 i 1882. Tranzyty Wenus występują parami, ale mniej niż jedna para na stulecie, a obserwacja tranzytów w 1761 a 1769 był bezprecedensową międzynarodową operacją naukową, w tym obserwacjami Jamesa Cooka i Charlesa Greena z Tahiti. Pomimo wojny siedmioletniej dziesiątki astronomów wysłano do punktów obserwacyjnych na całym świecie, co wiązało się z dużymi kosztami i osobistym niebezpieczeństwem: kilku z nich zginęło podczas tych wysiłków. Różne wyniki zostały zebrane przez Jérôme'a Lalande'a, aby uzyskać wartość paralaksy słonecznej wynoszącą 8,6 ″ . Karl Rudolph Powalky oszacował 8,83 ″ w 1864 roku.

Data metoda A /Gm Niepewność
1895 aberracja 149,25 0,12
1941 paralaksa 149.674 0,016
1964 radar 149.5981 0,001
1976 telemetria 149.597 870 0,000 001
2009 telemetria 149.597 870 700 0,000 000 003

Inna metoda polegała na wyznaczeniu stałej aberracji . Simon Newcomb przywiązywał dużą wagę do tej metody, wyprowadzając swoją powszechnie akceptowaną wartość 8,80 ″ dla paralaksy słonecznej (blisko współczesnej wartości 8,794 143 ″ ), chociaż Newcomb wykorzystał również dane z tranzytów Wenus. Newcomb współpracował również z AA Michelsonem przy pomiarze prędkości światła za pomocą sprzętu naziemnego; w połączeniu ze stałą aberracji (która jest związana z czasem świecenia na jednostkę odległości), dało to pierwszy bezpośredni pomiar odległości Ziemia-Słońce w kilometrach. Wartość Newcomba dla paralaksy słonecznej (oraz dla stałej aberracji i stałej grawitacyjnej Gaussa) została włączona do pierwszego międzynarodowego systemu stałych astronomicznych w 1896 r., Który obowiązywał do obliczania efemeryd do 1964 r. Nazwa „jednostka astronomiczna” wydaje się, że po raz pierwszy użyto go w 1903 r. [ nieudana weryfikacja ]

Odkrycie bliskiej Ziemi asteroidy 433 Eros i jej przejście w pobliżu Ziemi w latach 1900–1901 umożliwiło znaczną poprawę pomiarów paralaksy. Kolejny międzynarodowy projekt pomiaru paralaksy 433 Erosa podjęto w latach 1930–1931.

Bezpośrednie pomiary radarowe odległości do Wenus i Marsa stały się dostępne na początku lat sześćdziesiątych. Wraz z ulepszonymi pomiarami prędkości światła wykazały one, że wartości paralaksy słonecznej i stałej aberracji Newcomba były ze sobą niespójne.

Rozwój

Jednostka astronomiczna jest używana jako linia bazowa trójkąta do pomiaru paralaks gwiazd (odległości na obrazie nie są zgodne ze skalą)

Odległość jednostkową A (wartość jednostki astronomicznej w metrach) można wyrazić za pomocą innych stałych astronomicznych:

gdzie G jest newtonowską stałą grawitacji , M ☉ jest masą Słońca, k jest wartością liczbową stałej grawitacji Gaussa, a D jest okresem jednego dnia. Słońce nieustannie traci masę, wypromieniowując energię, więc orbity planet stale rozszerzają się na zewnątrz od Słońca. Doprowadziło to do wezwań do porzucenia jednostki astronomicznej jako jednostki miary.

Ponieważ prędkość światła ma dokładnie określoną wartość w jednostkach SI, a stała grawitacyjna Gaussa k jest ustalona w astronomicznym systemie jednostek , pomiar czasu świetlnego na jednostkę odległości jest dokładnie równoważny pomiarowi iloczynu G × M ☉ w jednostkach SI. Stąd możliwe jest konstruowanie efemeryd w całości w jednostkach SI, co w coraz większym stopniu staje się normą.

Analiza pomiarów radiometrycznych z 2004 roku w wewnętrznym Układzie Słonecznym sugeruje, że świecki wzrost odległości jednostkowej był znacznie większy niż można to wytłumaczyć promieniowaniem słonecznym, + 15 ± 4 metry na stulecie.

Pomiary świeckich zmian jednostki astronomicznej nie są potwierdzone przez innych autorów i są dość kontrowersyjne. Ponadto od 2010 roku jednostka astronomiczna nie jest szacowana na podstawie efemeryd planetarnych.

Przykłady

Poniższa tabela zawiera niektóre odległości podane w jednostkach astronomicznych. Zawiera kilka przykładów z odległościami, które normalnie nie są podawane w jednostkach astronomicznych, ponieważ są albo za krótkie, albo o wiele za długie. Odległości zwykle zmieniają się w czasie. Przykłady są wymienione według rosnącej odległości.

Obiekt Długość lub odległość (au) Zakres Komentarz i punkt odniesienia ref
Sekunda świetlna 0,0019 – odległość pokonuje światło w ciągu jednej sekundy –
Odległość księżycowa 0,0026 – średnia odległość od Ziemi (którą pokonanie misji Apollo zajęło około 3 dni) –
Promień słoneczny 0,005 – promień Słońca ( 695 500 km , 432 450 mil , stokrotność promienia Ziemi lub dziesięciokrotność średniego promienia Jowisza) –
minuta świetlna 0,12 – odległość pokonuje światło w ciągu jednej minuty –
Rtęć 0,39 – średnia odległość od Słońca –
Wenus 0,72 – średnia odległość od Słońca –
Ziemia 1.00 – średnia odległość orbity Ziemi od Słońca ( światło słoneczne podróżuje przez 8 minut i 19 sekund, zanim dotrze do Ziemi) –
Mars 1,52 – średnia odległość od Słońca –
Jowisz 5.2 – średnia odległość od Słońca –
Godzina świetlna 7.2 – odległość pokonuje światło w ciągu godziny –
Saturn 9.5 – średnia odległość od Słońca –
Uran 19.2 – średnia odległość od Słońca –
Pas Kuipera 30 – Wewnętrzna krawędź zaczyna się na około 30 au
Neptun 30.1 – średnia odległość od Słońca –
Eris 67,8 – średnia odległość od Słońca –
Podróżnik 2 132 – odległość od Słońca w lutym 2023 r
Podróżnik 1 159 – odległość od Słońca w lutym 2023 r
jasny dzień 173 – odległość pokonuje światło w ciągu jednego dnia –
Rok świetlny 63 241 – odległość, jaką pokonuje światło w ciągu jednego roku juliańskiego (365,25 dni) –
Chmura Oorta 75 000 ± 25 000 odległość zewnętrznej granicy chmury Oorta od Słońca (szacowana, odpowiada 1,2 roku świetlnego) –
Parsek 206 265 – jeden parsek . Parsek jest definiowany w jednostkach astronomicznych, służy do pomiaru odległości poza zakresem Układu Słonecznego i wynosi około 3,26 lat świetlnych: 1 szt. = 1 au/tan (1″)
Proxima Centauri 268 000 ± 126 odległość do najbliższej gwiazdy Układu Słonecznego –
Centrum Galaktyki 1 700 000 000 – odległość od Słońca do centrum Drogi Mlecznej –
Uwaga: liczby w tej tabeli są na ogół zaokrąglone, szacunki, często przybliżone szacunki i mogą znacznie różnić się od innych źródeł. Tabela zawiera również inne jednostki długości dla porównania.

Zobacz też

Dalsza lektura

Linki zewnętrzne

Pobrane z „ https://en.wikipedia.org/w/index.php?title=Astronomical_unit&oldid=1138471970 ”