Twierdzenie o projekcji-plastrze

Twierdzenie Fouriera o plasterku

W matematyce twierdzenie o przekroju projekcji , twierdzenie o przekroju centralnym lub twierdzenie Fouriera o przekroju w dwóch wymiarach stwierdza, że ​​wyniki następujących dwóch obliczeń są równe:

• Weź dwuwymiarową funkcję f ( r ), rzuć ją (np. używając transformaty Radona ) na (jednowymiarową) prostą i wykonaj transformatę Fouriera tego rzutowania.
• Weź tę samą funkcję, ale najpierw wykonaj dwuwymiarową transformatę Fouriera, a następnie przetnij ją przez jej początek, który jest równoległy do ​​linii rzutowania.

W kategoriach operatorskich, jeśli

• F ₁ i F ₂ to 1- i 2-wymiarowe operatory transformacji Fouriera wspomniane powyżej,
• P ₁ jest operatorem projekcji (który rzutuje funkcję 2-D na linię 1-D),
• S ₁ jest operatorem plasterka (który wyodrębnia z funkcji centralny plasterek 1-D),

Następnie

${\ Displaystyle F_ {1} P_ {1} = S_ {1} F_ {2}.}$

Pomysł ten można rozszerzyć na wyższe wymiary.

Twierdzenie to stosuje się na przykład w analizie medycznych tomografii komputerowej , gdzie „projekcją” jest obraz rentgenowski narządu wewnętrznego. Transformaty Fouriera tych obrazów są postrzegane jako wycinki transformaty Fouriera trójwymiarowej gęstości narządu wewnętrznego i te wycinki można interpolować w celu zbudowania pełnej transformaty Fouriera tej gęstości. Następnie stosuje się odwrotną transformatę Fouriera w celu odzyskania trójwymiarowej gęstości obiektu. Technikę tę po raz pierwszy opracował Ronald N. Bracewell w 1956 roku dla problemu radioastronomicznego.

Twierdzenie o projekcji w N wymiarach

W N wymiarach twierdzenie o przekroju projekcyjnym stwierdza, że ​​transformata Fouriera rzutu N -wymiarowej funkcji f ( r ) na m -wymiarową podrozmaitość liniową jest równa m -wymiarowemu wycinkowi N -wymiarowej transformaty Fouriera funkcja ta składa się z m -wymiarowej podrozmaitości liniowej mającej początek w przestrzeni Fouriera, która jest równoległa do podrozmaitości rzutowania. W kategoriach operatorskich:

${\ Displaystyle F_ {m} P_ {m} = S_ {m} F_ {N}. \,}$

Uogólnione twierdzenie Fouriera o przekroju

Oprócz uogólniania na N wymiarów, twierdzenie o przekroju projekcyjnym można dalej uogólniać poprzez dowolną zmianę podstawy. Dla wygody zapisu uważamy, że zmianę podstawy reprezentujemy jako B , odwracalną macierz N na N działającą na N -wymiarowych wektorach kolumnowych. Następnie uogólnione twierdzenie Fouriera o przekroju można sformułować jako

${\ Displaystyle F_ {m} P_ {m} B = S_ {m} {\ Frac {B ^ {-T}} {|B ^ {-T} |}}F_ {N}}$

gdzie jest transpozycją odwrotności zmiany transformacji podstawy ${\ displaystyle B ^ {-T} = (B ^ {-1}) ^ {T}}$

Dowód w dwóch wymiarach

Graficzna ilustracja twierdzenia o plasterku projekcji w dwóch wymiarach. f ( r ) i F ( k ) są parami dwuwymiarowej transformacji Fouriera. Rzut f ( r ) na oś x jest całką f ( r ) wzdłuż linii wzroku równoległych do osi y i jest oznaczony jako p ( x ). Przekrój przez F ( k ) znajduje się na k _x oś, która jest równoległa do osi x i oznaczona jako s ( k _x ). Twierdzenie o przekroju projekcyjnym stwierdza, że ​​p ( x ) i s ( k _x ) są parami jednowymiarowej transformaty Fouriera.

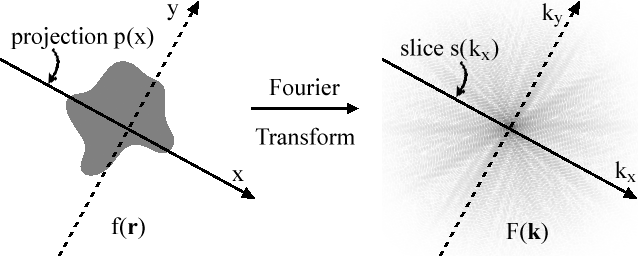
Twierdzenie o przekroju projekcyjnym można łatwo udowodnić dla przypadku dwóch wymiarów. Bez utraty ogólności możemy przyjąć, że linia rzutowania jest osią x . Nie ma utraty ogólności, ponieważ jeśli użyjemy przesuniętej i obróconej linii, prawo nadal obowiązuje. Użycie przesuniętej linii (w y) daje taki sam rzut, a zatem takie same wyniki 1D transformacji Fouriera. Obrócona funkcja jest parą Fouriera obróconej transformaty Fouriera, dla której twierdzenie ponownie jest spełnione.

Jeśli f ( x , y ) jest funkcją dwuwymiarową, to rzut f ( x , y ) na oś x wynosi p ( x ) gdzie

${\ Displaystyle p (x) = \ int _ {- \ infty} ^ {\ infty} f (x, y) \, dy.}$

Transformata Fouriera wynosi fa $\ displaystyle f (x, y)}$

${\ Displaystyle F (k_ {x}, k_ {y}) = \ int _ {- \ infty } ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} f (x, y) \, e^{-2\pi i(xk_{x}+yk_{y})}\,dxdy.}$

Następnie plasterek jest ${\ displaystyle s (k_ {x})}$

${\ displaystyle s (k_ {x}) = F(k_{x},0)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\ pi ixk_{x}}\,dxdy}$

${\ Displaystyle = \ int _ {- \ infty} ^ {\ infty} \ lewo [\ int _ {- \infty }^{\infty }f(x,y)\,dy\right]\,e^{-2\pi ixk_{x}}dx}$

${\ Displaystyle = \ int _ {- \ infty} ^ {\ infty} p (x) \, e ^ {- 2 \ pi ixk_ {x}} dx}$

co jest po prostu transformatą Fouriera p ( x ). Dowód na wyższe wymiary można łatwo uogólnić na podstawie powyższego przykładu.

Cykl FHA

Jeśli dwuwymiarowa funkcja f ( r ) jest kołowo symetryczna, można ją przedstawić jako f ( r ), gdzie r = | r |. W tym przypadku rzut na dowolną linię projekcji będzie transformatą Abela f ( r ). Dwuwymiarowa transformata Fouriera f ( r ) będzie funkcją kołowo symetryczną określoną przez transformatę Hankla zerowego rzędu f ( r ), co będzie zatem również reprezentować dowolny przekrój początku. Twierdzenie o projekcji-plasterku stwierdza następnie, że transformata Fouriera rzutu jest równa plasterkowi lub

${\ Displaystyle F_ {1} A_ {1} = H,}$

gdzie A ₁ reprezentuje operator transformacji Abela rzutujący dwuwymiarową funkcję kołowo symetryczną na linię jednowymiarową, F ₁ reprezentuje 1-D operator transformacji Fouriera, a H oznacza operator transformacji Hankla zerowego rzędu.

Rozszerzenie do belki wachlarzowej lub przekładnika stożkowego

Twierdzenie o projekcji jest odpowiednie do rekonstrukcji obrazu CT za pomocą projekcji wiązek równoległych. Nie dotyczy to bezpośrednio wiązek wachlarzowych ani stożkowych CT. Twierdzenie zostało rozszerzone na rekonstrukcję obrazu CT za pomocą wiązki wachlarzowej i wiązki stożkowej przez Shuang-ren Zhao w 1995 roku.

Zobacz też

• Transformata Radona § Związek z transformatą Fouriera

Dalsza lektura

•    Bracewell, Ronald N. (1990). „Przekształcenia numeryczne”. Nauka . 248 (4956): 697–704. Bibcode : 1990Sci...248..697B . doi : 10.1126/science.248.4956.697 . PMID 17812072 . S2CID 5643835 .
• Bracewell, Ronald N. (1956). „Integracja pasków w radioastronomii” . sierpień J. Fiz . 9 (2): 198. Bibcode : 1956AuJPh...9..198B . doi : 10.1071/PH560198 .
•   Gaskill, Jack D. (2005). Systemy liniowe, transformaty Fouriera i optyka . John Wiley & Sons, Nowy Jork. ISBN 978-0-471-29288-3 .
• Ng, Ren (2005). „Fotografia Fouriera” (PDF) . Transakcje ACM na grafice . 24 (3): 735–744. doi : 10.1145/1073204.1073256 .
• Zhao, Shuang-Ren; Hallinga, Horsta (1995). „Rekonstrukcja rzutów wiązek stożkowych ze ścieżką swobodnego źródła za pomocą uogólnionej metody Fouriera”. Materiały z Międzynarodowego spotkania w sprawie w pełni trójwymiarowej rekonstrukcji obrazu w radiologii i medycynie nuklearnej z 1995 r .: 323–7.
•   Garces, Daissy H.; Rhodes, William T.; Peña, Néstor (2011). „Twierdzenie o projekcji-plasterku: notacja zwarta”. Journal of Optical Society of America A. 28 (5): 766–769. Kod Biblijny : 2011JOSAA..28..766G . doi : 10.1364/JOSAA.28.000766 . PMID 21532686 .

Linki zewnętrzne

• Twierdzenie Fouriera o plasterku (wideo). Część kursu „Tomografia komputerowa i zestaw narzędzi ASTRA”. Uniwersytet w Antwerpii . 10 września 2015 r.