Ekspansja wirusowa

Klasyczna ekspansja wirialna wyraża ciśnienie P układu wielocząstkowego w równowadze jako szereg potęgowy w gęstości :

$${\ Displaystyle Z \ równoważnik {\ Frac {P} {RT \ rho}} = A + B \ rho + C \ rho ^ {2} + \cdots}$$

gdzie nazywa się $ściśliwości$ . Jest to wirialne równanie stanu, najbardziej ogólna funkcja związana z ciśnieniem P , gęstością ρ i temperaturą T płynów. Po raz pierwszy został zaproponowany przez Kamerlingha Onnesa . Współczynnik ściśliwości jest wielkością bezwymiarową, wskazującą, jak bardzo rzeczywisty płyn odbiega od gazu doskonałego. A jest pierwszym współczynnikiem wirialnym, który ma stałą wartość 1. Stwierdza on, że przy małej gęstości wszystkie płyny zachowują się jak gazy doskonałe. Współczynniki wirialne B , C , D itd. są zależne od temperatury i są ogólnie przedstawiane jako szeregi Taylora wyrażone jako 1/ T .

Drugi i trzeci współczynnik wirialny

Drugi, B i trzeci, C , współczynniki wirialne były szeroko badane i zestawione w tabelach dla wielu płynów przez ponad sto lat. Dwie najbardziej obszerne kompilacje znajdują się w książkach Dymonda. oraz NIST Thermo Data Engine Database i jej Web Thermo Tables. W zestawieniach tych zawarte są tablice drugiego i trzeciego współczynnika wirialnego wielu płynów.

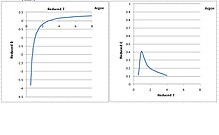
Drugi i trzeci współczynnik wirialny argonu

Drugi i trzeci współczynnik wirialny w funkcji temperatury przedstawiono na poniższym rysunku dla argonu. Zredukowana temperatura i zmniejszone współczynniki wirialne, skalowane według odpowiednich właściwości krytycznych, są bezwymiarowe. Zauważ na rysunku, że drugi współczynnik wirialny maleje monotonicznie wraz ze spadkiem temperatury. Jednak trzeci współczynnik wirialny ma kształt dzwonu. Zwiększa się, gdy temperatura spada do temperatury krytycznej, następnie przechodzi przez szczyt i gwałtownie spada do zera, gdy temperatura obniża się od punktu krytycznego do punktu potrójnego. Spadek poniżej temperatury krytycznej jest fizycznie nieuzasadniony. Dzieje się tak, ponieważ trzeci współczynnik wirialny teoretycznie reprezentuje siłę odpychania między cząsteczkami, która ma wzrosnąć w niższej temperaturze, gdy cząsteczki są dociskane do siebie. Opisane właśnie zachowania są podobne do wielu innych gazów, jak pokazano na poniższym rysunku.

Powód, dla którego trzeci współczynnik wirialny spada poniżej temperatury krytycznej, jest następujący. Zasadniczo izotermy PρT są mierzone w fazie gazowej. Poniżej temperatury krytycznej faza gazowa skrapla się i współistnieje z fazą ciekłą, a izoterma PρT staje się płaska. Ciśnienie nasycenia nie zmienia się, dopóki gaz nie skrapla się całkowicie do stanu ciekłego, a następnie ciśnienie wzrasta wraz ze wzrostem gęstości. Istnieje duża luka między czystą fazą gazową a czystą fazą ciekłą, w przypadku której nie są dostępne żadne użyteczne dane dotyczące ciśnienia, z wyjątkiem ciśnienia nasycenia. Gdyby analizować tylko dane w fazie gazowej, trzeci współczynnik wirialny staje się bardzo mały, ponieważ izoterma PρT jest prawie liniowa w fazie gazowej. Jeśli jednak zostaną uwzględnione punkty danych w czystej fazie ciekłej, regresja drugiego rzędu dałaby duży trzeci współczynnik wirialny. Wyprowadzony w ten sposób trzeci współczynnik wirialny wzrastałby monotonicznie w miarę obniżania temperatury od punktu krytycznego do punktu potrójnego.

Oczekiwanie, że trzeci współczynnik wirialny jest monotonicznie rosnącą funkcją 1/ T , można zweryfikować za pomocą równań stanu, które dokładnie przewidywały izotermy PρT w obszarze nasycenia, w którym współistnieją fazy gazowa i ciekła.

Przekształcanie równań stanu w postać wirialną

Większość równań stanu można przeformułować i ująć w równania wirialne w celu oceny i porównania ich niejawnych drugich i trzecich współczynników wirialnych. Przełomowe stanu Van der Waalsa zostało zaproponowane w 1873 roku:

$${\ Displaystyle P = {\ Frac {RT} {\ lewo (vb \ prawo)}} - {\ Frac {a} {v ^ {2}}}}$$

gdzie v = 1/ ρ jest objętością molową. Można go uporządkować, rozszerzając 1/( v - b ) do szeregu Taylora:

$${\ Displaystyle Z = 1 + \ lewo (b- {\ Frac {a} {RT}} \ prawej) \ rho +b^{2}\rho ^{2}+b^{3}\rho ^{3}+\cdots }$$

W równaniu Van der Waalsa drugi współczynnik wirialny ma z grubsza prawidłowe zachowanie, ponieważ maleje monotonicznie, gdy temperatura jest obniżana. Trzeci i wyższe współczynniki wirialne są niezależne od temperatury i nie są poprawne, zwłaszcza w niskich temperaturach.

Niemal wszystkie kolejne równania stanu wyprowadzone z równania Van der Waalsa, takie jak równania Dietericiego, Berthelota, Redlicha-Kwonga, Peng-Robinsona itp., cierpią z powodu osobliwości wprowadzonej przez 1/( v - b ) . Dlatego nie mogą dokładnie reprezentować izoterm PρT w temperaturach poniżej temperatury krytycznej. Wiele z nich daje odpowiednie drugie współczynniki wirialne, ale większość daje nieprawidłowe trzecie współczynniki wirialne .

Inne równania stanu, zapoczątkowane przez Beattiego-Bridgemana, są jednak bliżej spokrewnione z równaniami wirialnymi i okazują się dokładniejsze w przedstawianiu zachowania płynów zarówno w fazie gazowej, jak i ciekłej. Można je przeformułować w wirialne równania stanu i porównać ze sobą. Równanie stanu Beattiego-Bridgemana, zaproponowane w 1928 r.,

$${\ Displaystyle p = {\ Frac {RT} {v ^ {2}}} \ lewo (1- {\ Frac {c}{vT^{3}}}\right)(v+B)-{\frac {A}{v^{2}}}}$$

Gdzie

• ${\ Displaystyle A = A_ {0} \ lewo (1- {\ Frac {a} {v}} \ prawej)}$
• ${\ Displaystyle B = B_ {0} \ lewo (1- {\ Frac {b} {v}} \ prawej)}$

można przeorganizować:

$${\ Displaystyle Z = 1 + \ lewo (B_ {0} - {\ Frac {A_ {0}} {RT}} - {\ Frac {c} {T ^ {3}}} \ prawej) \ rho - \ left(B_{0}b-{\frac {A_{0}a}{RT}}+{\frac {B_{0}c}{T^{3}}}\right)\rho ^{2} +\left({\frac {B_{0}bc}{T^{3}}}\right)\rho ^{3}}$$

To równanie stanu dobrze reprezentuje drugi współczynnik wirialny. Jednak trzeci współczynnik wirialny ma zły znak. W związku z tym nie reprezentuje izoterm bliskich i niższych od temperatury krytycznej.

Równanie Benedicta-Webba-Rubina stanu z 1940 roku przedstawia lepsze izotermy poniżej temperatury krytycznej:

$${\ Displaystyle Z = 1 + \ lewo (B_ {0} - {\ Frac {A_ {0}} {RT}} - {\ Frac {C_ {0}} {RT ^ {3}} }\right)\rho +\left(b-{\frac {a}{RT}}\right)\rho ^{2}+\left({\frac {\alpha a}{RT}}\right) \rho ^{5}+{\frac {c\rho ^{2}}{RT^{3}}}\left(1+\gamma \rho ^{2}\right)\exp \left(-\ gamma \rho ^{2}\right)}$$

Więcej ulepszeń osiąga Starling w 1972 roku:

$${\ Displaystyle Z = 1 + \ lewo (B_ {0} - {\ Frac {A_ {0}}} RT}}-{\frac {C_{0}}{RT^{3}}}+{\frac {D_{0}}{RT^{4}}}-{\frac {E_{0}}{ RT^{5}}}\right)\rho +\left(b-{\frac {a}{RT}}-{\frac {d}{RT^{2}}}\right)\rho ^{ 2}+\alpha \left({\frac {a}{RT}}+{\frac {d}{RT^{2}}}\right)\rho ^{5}+{\frac {c\rho ^{2}}{RT^{3}}}\left(1+\gamma \rho ^{2}\right)\exp \left(-\gamma \rho ^{2}\right)}$$

Poniżej przedstawiono wykresy zredukowanych drugich i trzecich współczynników wirialnych w funkcji obniżonej temperatury według Starlinga:

Drugi i trzeci współczynnik wirialny dla 12 płynów

Wykładnicze wyrażenia w dwóch ostatnich równaniach korygują trzeci współczynnik wirialny, tak że izotermy w fazie ciekłej mogą być reprezentowane poprawnie. Składnik wykładniczy $przez$ pierwsze wyrazy z szeregu rozwinięć Taylora i pomnożyli to ${\ Displaystyle 1 + \ gamma \ rho ^ {2}}$ , wynik to ${\ Displaystyle 1- \ gamma ^ {2} \ rho ^ {4}}$ . W ten sposób wnosi $składnik do$ ósmego współczynnika wirialnego, który można

Po rozwinięciu wyrazów wykładniczych równania stanu Benedicta-Webba-Rubina i Starlinga mają następującą postać:

$${\ Displaystyle Z = 1 + b \ rho _ {r} + c \ rho _ {r} ^ {2} + f \ rho _ {r }^{5}}$$

Czwarty i piąty współczynnik wirialny wynosi zero. Po trzecim członie wirialnym kolejnym znaczącym członem jest szósty współczynnik wirialny. Wydaje się, że pierwsze trzy człony wirialne dominują we współczynniku ściśliwości płynów, aż do i $rho _ {c}}$$2,0$ ρ do .

Ponowna analiza danych przez Starling

Po ponownej analizie danych zgłoszonych przez Starling, współczynniki wirialne są najlepiej reprezentowane przez

$${\ Displaystyle b = b_ {0} + {\ Frac {b_ {1}} {t_ {r}}} + {\ Frac {b_{2}}{t_{r}^{2}}}+{\frac {b_{3}}{t_{r}^{3}}}}$$

$${\ Displaystyle c = c_ {0} + {\ Frac {c_ {1}} {t_ {r}}} + {\ Frac {c_{2}}{t_{r}^{2}}}+{\frac {c_{3}}{t_{r}^{3}}}}$$

$${\ Displaystyle f = f_ {0} + {\ Frac {f_ {1}} {t_ {r}}}}$$

b i c można określić za pomocą prostej analizy regresji drugiego rzędu z eksperymentalnych izoterm PρT. ${\ Displaystyle b_ {0} -b_ {3}}$ i ${\ Displaystyle c_ {0} -c_ {3}}$ można następnie określić za pomocą analizy regresji trzeciego rzędu na b i c . ${\ displaystyle f_ {0} -f_ {1}}$ można następnie określić, analizując pozostałości we współczynniku ściśliwości po usunięciu pierwszych trzech terminów wirialnych z równania wirialnego. Dane Starling są ponownie analizowane, a wyniki przedstawiono w poniższej tabeli. Wszystkie te współczynniki są bezwymiarowe, wszystkie są skalowane z krytycznymi objętościami molowymi i krytyczną temperaturą.

Płyn	${\ displaystyle b_ {0}}$	${\ displaystyle b_ {1}}$	${\ displaystyle b_ {2}}$	${\ displaystyle b_ {3}}$	${\ displaystyle c_ {0}}$	${\ displaystyle c_ {1}}$	${\ displaystyle c_ {2}}$	${\ displaystyle c_ {3}}$	${\ displaystyle f_ {0}}$	${\ displaystyle f_ {1}}$
Metan	0,440	−1,171	−0,236	−0,210	0,364	−0,275	−0,014	0,396	0,0319	1,71 × 10-03 _
Etan	0,330	−0,806	−0,363	−0,378	0,553	−0,675	−0,038	0,680	0,0461	2,63 × 10-03 _
propan	0,288	−0,706	−0,245	−0,575	0,532	−0,546	−0,308	0,843	0,0334	1,89 × 10-02 _
n-butan	0,377	−0,916	−0,115	−0,610	0,547	−0,519	−0,347	0,871	0,0305	2,04 × 10-02 _
i-butan	0,438	−1,051	−0,172	−0,401	0,483	−0,342	−0,021	0,538	0,0194	1,19 × 10-03 _
n-pentan	0,481	−1,056	−0,166	−0,560	0,668	−0,720	−0,204	0,841	0,0411	1,17 × 10-02 _
i-pentan	0,242	−0,674	−0,306	−0,520	0,815	−0,943	−0,194	0,868	0,0484	9,99 × 10-03 _
n-Heksan	0,435	−0,636	−0,358	−0,759	0,848	−1,275	−0,105	1.120	0,0604	4,98 × 10-03 _
n-heptan	0,493	−0,798	−0,636	−0,428	0,589	−0,738	−0,017	0,814	0,0508	1,21 × 10-03 _
n-oktan	0,600	−0,744	−0,456	−0,763	0,174	−0,197	−0,272	0,919	0,0144	1,99 × 10-02 _
Azot	0,502	−1,380	0,092	−0,333	0,400	−0,276	−0,027	0,322	0,0279	2,72 × 10-03 _
CO2 _	0,178	−0,044	−1,517	0,039	0,428	−0,422	−0,008	0,687	0,0490	9,52 × 10-04 _
H2S _ _	0,191	−0,927	−0,078	−0,366	1.093	−1,227	−0,001	0,577	0,0578	8,37 × 10-05 _

Sześcienne wirialne równanie stanu

Trójczłonowe równanie wirialne lub sześcienne wirialne równanie stanu

$${\ Displaystyle Z = 1 + B \ rho + C \ rho ^ {2}}$$

ma prostotę równania stanu Van der Waalsa bez osobliwości w v = b . Teoretycznie drugi współczynnik wirialny reprezentuje siły przyciągania dwucząsteczkowego, a trzeci człon wirialny reprezentuje siły odpychające między trzema cząsteczkami w bliskim kontakcie. Intuicyjnie powinniśmy oczekiwać, że B stanie się ujemny w niskiej temperaturze, podczas gdy C pozostanie dodatnie, aby zrównoważyć efekt B i popycha Z , a tym samym ciśnienie do wysokich wartości, jak ρ wzrasta.

Za pomocą tego sześciennego równania wirialnego współczynniki B i C można rozwiązać w postaci zamkniętej. Nałożenie warunków krytycznych:

$${\ Displaystyle {\ Frac {\ operatorname {d} P} {\ operatorname {d} v}} = 0 \ qquad {\ tekst {i}} \ qquad { \frac {\mathrm {d} ^{2}P}{\mathrm {d} v^{2}}}=0}$$

sześcienne równanie wirialne można rozwiązać, otrzymując:

$${\ Displaystyle B = - v_ {c},}$$

$${\ Displaystyle C = {\ Frac {v_ {c} ^ {2}} {3}}}$$

I

$${\ Displaystyle Z_ {c} = {\ Frac {P_ {c} v_ {c}} {RT_ {c}}} = {\ Frac {1} {3}}.}$$

${\ displaystyle Z_ {c}}$ wynosi zatem 0,333, w porównaniu do 0,375 z równania stanu Van der Waalsa.

Pomiędzy punktem krytycznym a punktem potrójnym znajduje się obszar nasycenia płynów. W tym obszarze faza gazowa współistnieje z fazą ciekłą pod ciśnieniem nasycenia $T$ temperaturą nasycenia $_ {\ text {sat}}}$ . Pod ciśnieniem nasycenia faza $tekst$${g}} }$ objętość molową , a faza gazowa ma objętość molową . Odpowiednie gęstości molowe to ${\ Displaystyle \ rho _ {\ tekst {l}}}$ i ${\ Displaystyle \ rho _ {\ tekst {g}}}$ . Są to właściwości nasycenia potrzebne do obliczenia drugiego i trzeciego współczynnika wirialnego.

Prawidłowe równanie stanu musi dawać izotermę, która przecina poziomą linię ${\ Displaystyle P _ {\ tekst {sat}}}$ w ${\ displaystyle v _ {\ tekst {l}}}$ i ${\ displaystyle v _ {\ text {g}}}$ , na ${\ displaystyle T _ {\ text {sat}}}$ . Pod ${\ Displaystyle P _ {\ text {sat}}}$ i ${\ Displaystyle T _ {\ text {sat}}}$ , gaz jest w równowadze z cieczą. Oznacza to, że izoterma PρT ma trzy pierwiastki w ${\ displaystyle P _ {\ text {sat}}}$ . Sześcienne wirialne równanie stanu w ${\ Displaystyle T _ {\ text {sat}}}$ to:

$${\ Displaystyle P _ {\ tekst {sat}} = RT _ {\ tekst {sat}} \ lewo (1 + B \ rho + C \ rho ^ {2}\prawo)\rho}$$

Można to przeorganizować jako:

$${\ Displaystyle 1 - {\ Frac {RT _ {\ tekst {sat}}} {P _ {\ tekst {sat}}}} \ lewo (1+B\rho +C\rho ^{2}\right)\rho =0}$$

Współczynnik ${\ Displaystyle RT _ {\ text {sat}} / P _ {\ text {sat}}}$ to objętość gazu nasyconego zgodnie z prawem gazu doskonałego i można mu nadać unikalną nazwę ${\ displaystyle v ^ {\ tekst {identyfikator}}}$ :

$${\ Displaystyle v ^ {\ tekst {id}} = {\ Frac {RT _ {\ tekst {sat}}} {P _ {\ tekst {sat}}}}}$$

W obszarze nasycenia równanie sześcienne ma trzy pierwiastki i można je zapisać alternatywnie jako:

$${\ Displaystyle \ lewo (1-v_ {\ tekst {l}} \ rho \ prawo) \ lewo (1-v_ { \text{m}}\rho \right)\left(1-v_{\text{g}}\rho \right)=0}$$

co można rozwinąć jako:

$${\ Displaystyle 1- \ lewo (v_ {\ tekst {l}} + v _ {\ tekst {g}} + v_ {m} \ prawo) \ rho + \ lewo (v_ {\ tekst {l}} v_ {\ text{g}}+v_{\text{g}}v_{\text{m}}+v_{\text{m}}v_{\text{l}}\right)\rho ^{2}-v_ {\text{l}}v_{\text{g}}v_{\text{m}}\rho ^{3}=0}$$

${\ Displaystyle v _ {\ tekst {m}}}$ to objętość w stanie niestabilnym między ${\ displaystyle v _ {\ tekst {l}}}$ a ${\ displaystyle v _ {\ tekst {g}} }$ . Równania sześcienne są identyczne. Dlatego z terminów liniowych w tych równaniach można rozwiązać: ${\ displaystyle v_ {m}}$

$${\ Displaystyle v _ {\ tekst {m}} = v ^ {\ tekst {id}} -v_ {\ tekst {l}} -v _ {\ tekst {g}} }$$

Z wyrażeń kwadratowych B można rozwiązać:

$${\ Displaystyle B = - {\ Frac {\ lewo (v _ {\ tekst {l}} v _ {\ tekst {g}} +v_{\text{g}}v_{\text{m}}+v_{\text{m}}v_{\text{l}}\right)}{v^{\text{id}}}} }$$

A z wyrażeń sześciennych C można rozwiązać:

$${\ Displaystyle C = {\ Frac {v _ {\ tekst {l}} v _ {\ tekst {g}} v _ {\ tekst {m}}} {v ^ {\ tekst {ID}}}}}$$

Ponieważ ${\ displaystyle v _ {\ text {l}}}$ , ${\ displaystyle v _ {\ text {g}}}$ i ${\ displaystyle P _ {\ text {sat}}}$ zostały zestawione w tabeli dla wielu płyny z ${\ displaystyle T _ {\ text {sat}}}$ jako parametrem, B i C można obliczyć w obszarze nasycenia tych płynów. Wyniki są zasadniczo zgodne z wynikami obliczonymi z równań stanu Benedicta-Webba-Rubina i Starlinga. Jednak dokładność w B i C jest w dużym stopniu zależna od pomiarów i $}}$$}$ , które są bardzo trudne do wykonania dokładnie mierzyć w niskich temperaturach. Wprowadzone w ten sposób błędy pomiarowe do B i C należy wziąć pod uwagę, porównując otrzymane w ten sposób wartości z wartościami uzyskanymi z analizy regresji drugiego rzędu izoterm PρT.

Równowaga gaz-ciecz-ciało stałe

Sześcienne wirialne równanie stanu dokładnie przedstawia równowagę gaz-ciecz większości substancji od punktu krytycznego do punktu potrójnego, w którym zaczyna pojawiać się faza stała. Można go rozszerzyć, aby uwzględnić równowagę gaz-ciecz-ciało stałe:

$${\ Displaystyle P = {\ Frac {RT} {V}} \ lewo (1 + {\ Frac {B} {V}}+{\frac {C}{V^{2}}}+{\frac {U}{V^{n}}}+{\frac {W}{V^{2n}}}\ Prawidłowy)}$$

$równaniu$ pierwszy wyraz ciśnienie generowane przez energię kinetyczną Drugi $zasięgu$ . Trzeci termin ${\ textstyle {\ Frac {RTC} {V ^ {3}}}}$ reprezentuje odpychanie trójcząsteczkowe krótkiego zasięgu. Drugi człon obniża izotermę PVT w miarę zmniejszania objętości, podczas gdy trzeci człon podnosi izotermę. Gdy temperatura jest poniżej punktu krytycznego, izoterma PVT ma zatem wygięcie w kształcie litery S, co umożliwia współistnienie fazy ciekłej z przeważającą fazą gazową.

$} \textstyle {\frac {RTW}{V^{2n}}}}$ , gdybyśmy mieli obniżający izotermę PVT w fazie ciekłej i ${\textstyle {\frac {RTU}{V^{n$ pod względem wypchnięcia go z powrotem w górę, mogłaby powstać faza stała, ponieważ te dwa składniki tworzą kolejne zagięcie w kształcie litery S między cieczą a ciałem stałym. Wykazano, że takie zagięcie w kształcie litery S można zsyntetyzować za pomocą ${\ displaystyle \ delta}$ -funkcja taka jak funkcja Lorentza nad równaniem stanu van der Waalsa. Takim równaniem stanu trudno manipulować matematycznie. Natomiast równanie wirialne jest łatwiejsze w obsłudze.

Argon jest używany do realistycznej oceny tego rozszerzonego równania wirialnego dla równowagi gaz-ciecz-ciało stałe. Dane będą analizowane w postaci zredukowanej. Wszystkie zmienne PVT są skalowane według ich odpowiednich wartości krytycznych. Na podstawie zasady odpowiednich stanów oczekuje się, że wyniki będą miały zastosowanie do innych dobrze zachowujących się płynów. Odpowiednie dane dotyczące argonu podsumowano w poniższej tabeli:

Własność Argonu	Wartość	Zmniejszona wartość
Objętość punktu krytycznego (dm 3 /mol)	0,07459	1
Temperatura punktu krytycznego (K)	150.687	1
Ciśnienie w punkcie krytycznym (MPa)	4.863	1
Krytyczna ściśliwość	0,291	0,291
Objętość molowa pary punktu potrójnego (dm 3 /mol)	9.853	132.1
Objętość molowa cieczy punktu potrójnego (dm 3 /mol)	0,0282	0,378
Potrójna objętość molowa ciał stałych (dm 3 /mol)	0,246	0,330
Temperatura punktu potrójnego (K)	83.8058	0,553
Ciśnienie punktu potrójnego (MPa)	0,06889	0,0142

Gdy zmienne P , V i T zostaną zastąpione ich zredukowanymi odpowiednikami, ${\ textstyle p = {\ Frac {P} {P_ {c}}}}$ , ${\ textstyle v = {\ Frac {V} {V_ {c}}}}$ i ${\ textstyle t = {\ frac {T} {T_ {c}}}}$ , równanie wirialne przyjmuje następującą postać:

$${\ Displaystyle p = {\ Frac {t} {vZ_ {c}}} \ left(1-{\frac {b}{v}}+{\frac {c}{v^{2}}}-\left({\frac {v_{u}}{v}}\right)^ {n}+\left({\frac {v_{w}}{v}}\right)^{2n}\right)}$$

gdzie $\ textstyle Z_ {c} = {\ Frac {P_ {c} V_ {c}} {RT_ {c}}}}$ , ${\ textstyle b = {\ Frac {B} {V_ {c}}}}$ , ${\ textstyle c = {\ Frac {C} {V_ {c} ^ {2}}}}$ , ${\ textstyle U = v_ {u} ^ {n}}$ i ${\ textstyle W = v_ {w} ^ {2n}}$ . Zajmiemy się głównie warunkami w punkcie potrójnym argonu, gdzie b = 3,424 i c = 1,152 z wcześniejszego badania.

$V_ {w}} musi być$$musi$ większa niż objętość stałego argonu, 0,33, i znajdować się między objętościami ciekłego i stałego argonu. Początkowo ustawia się objętość ciała stałego, aby wytworzyć ostatnią ostro wznoszącą się krawędź izotermy, w której faza stała pojawia się przy bardzo $małej$ Wykładniczy n musi być wtedy określony tak, aby dolina w n -2 n potencjał musi mieścić się między objętościami ciała stałego (0,33) i cieczy (0,378). Po określeniu wykładniczego n wartość $.$ , aby spełnić regułę Gibbsa, która wymaga, aby energia swobodna Gibbsa fazy ciekłej i fazy stałej była równa pod potrójną liczbą punktowa temperatura i ciśnienie.

Aby wytworzyć fazę stałą w argonie, wykładnicza wartość n musi być bardzo duża, większa niż 20; w przeciwnym razie izoterma PVT nie wygięłaby się do kształtu litery S między cieczą a ciałem stałym. Najlepsze oszacowanie jest takie, że n = 30, ${\ Displaystyle t_ {t} = 0,553}$ , ${\ Displaystyle v_ {w} = 0,335}$ i ${\ Displaystyle v_ {u }=0,3443}$ . Izoterma jest pokazana na prawym rysunku, na którym trzy terminy wirialne są wykreślone osobno dla przejrzystości:

$${\ Displaystyle p_ {1} = {\ Frac {t_ {t}}} {vZ_ {c}}} \ lewo (1- {\ Frac {b}{v}}+{\frac {c}{v^{2}}}\right)}$$

$${\ Displaystyle p_ {2} = {\ Frac {t_ {t}} {vZ_ {c}}} \ lewo ({\ Frac {v_ {u}} {v}}\prawo)^{n}}$$

$${\ Displaystyle p_ {3} = {\ Frac {t_ {t}} {vZ_ {c}}} \ lewo ({\ Frac {v_ {w} }{v}}\prawo)^{2n}}$$

$${\ Displaystyle p = p_ {1} - p_ {2} + p_ {3}}$$

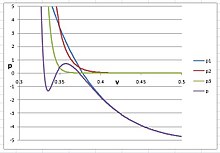
Izoterma PVT argonu przy n = 30 .

Na tym rysunku $reprezentuje$ sumę pierwszych trzech terminów wirialnych sześciennego równania wirialnego i pokazuje zachowanie argonu w jego fazie gazowej i ${\ Displaystyle p_ {2}}$ reprezentuje potencjał wniesiony z terminu ${\ textstyle \ lewo ({\ Frac {v_ {u}} {v}} \ prawej) ^ {n}}$ p ${\ displaystyle p_ {3}}$ reprezentuje wkład ${\ textstyle \ lewo ({\ Frac {v_ {w}}} {v}} \ prawo) ^ {2n}}$ termin. Kiedy n ${\ displaystyle p_ {1}}$ 30, kolidowałoby to z $i$ znacznie zmniejszałoby objętość cieczy

Zaskakujące jest to, że n musi być większe niż 20, aby wytworzyć fazę stałą. Powszechnie wiadomo, że potencjał Lenarda-Jonesa 6-12 można wykorzystać do obliczenia drugiego współczynnika wirialnego z zasad mechaniki kwantowej. Rozumowanie mechaniki kwantowej wiąże drugi współczynnik wirialny z przyciąganiem dwucząsteczkowym, a trzeci współczynnik z odpychaniem trójcząsteczkowym itp. W ciekłej fazie argonu jeden atom jest otoczony 12 najbliższymi sąsiadami i do 32 najbliższymi sąsiadami. W fazie stałej wszystkie atomy są zablokowane, a liczba oddziałujących na siebie sąsiadów jest nieskończona. Dlatego n = 30 lub nawet więcej jest rozsądne.

W rezultacie mamy wirialne równanie stanu opisujące ilościowo równowagę gaz-ciecz-ciało stałe dla argonu i wszystkich płynów, które przestrzegają zasady odpowiednich stanów, w punkcie potrójnym:

$${\ Displaystyle p = {\ Frac {t_ {t}} {vZ_ {c}}} \left(1-{\frac {3,424}{v}}+{\frac {1,152}{v^{2}}}-\left({\frac {0,3443}{v}}\right)^{30 }+\lewo({\frac {0.3350}{v}}\prawo)^{60}\prawo)}$$

Wirialne równania stanu

Na podstawie równań stanu Benedicta-Webba-Rubina i Starlinga ustalono, że najlepsze wirialne równanie stanu powinno mieć postać

$${\ Displaystyle Z = 1 + b \ rho _ {r} + c \ rho _ {r} ^ {2} + f \ rho _ {r} ^ {5}.}$$

Drugi i trzeci współczynnik wirialny w tym równaniu można obliczyć z eksperymentalnych danych PρT przy użyciu regresji liniowej . Po usunięciu pierwszych trzech terminów wirialnych, pozostałość we współczynniku ściśliwości Z można następnie wykorzystać do uzyskania szóstego współczynnika wirialnego.

Zobacz też

• Twierdzenie wirialne
• Mechanika statystyczna
• Równanie stanu