Wielki zespół kanoniczny

W mechanice statystycznej wielki zespół kanoniczny (znany również jako zespół makrokanoniczny ) jest zespołem statystycznym używanym do reprezentowania możliwych stanów układu mechanicznego cząstek znajdujących się w równowadze termodynamicznej (termicznej i chemicznej) ze zbiornikiem. O systemie mówi się, że jest otwarty w tym sensie, że może wymieniać energię i cząstki ze zbiornikiem, tak że różne możliwe stany układu mogą różnić się zarówno całkowitą energią, jak i całkowitą liczbą cząstek. Objętość, kształt i inne współrzędne zewnętrzne układu są takie same we wszystkich możliwych stanach układu.

Zmiennymi termodynamicznymi wielkiego zespołu kanonicznego są potencjał chemiczny (symbol: µ ) i temperatura bezwzględna (symbol: T ) . Zespół jest również zależny od zmiennych mechanicznych, takich jak objętość (symbol: V ) , które wpływają na charakter stanów wewnętrznych systemu. Zespół ten jest zatem czasami nazywany zespołem µVT , ponieważ każda z tych trzech wielkości jest stałą zespołu.

Podstawy

Mówiąc prościej, wielki zespół kanoniczny przypisuje prawdopodobieństwo P do każdego odrębnego mikrostanu określonego przez następujący wykładniczy:

${\ Displaystyle P = e ^ {\ Frac {\ Omega + \ mu NE} {kT}}}$

gdzie N to liczba cząstek w mikrostanie, a E to całkowita energia mikrostanu. k jest stałą Boltzmanna .

Liczba Ω jest znana jako wielki potencjał i jest stała dla zespołu. Jednak prawdopodobieństwa i Ω będą się różnić, jeśli wybrane zostaną różne µ , V , T. Wielki potencjał Ω pełni dwie role: zapewnia współczynnik normalizacji dla rozkładu prawdopodobieństwa (prawdopodobieństwa w całym zestawie mikrostanów muszą sumować się do jednego); i wiele ważnych średnich zespołowych można obliczyć bezpośrednio z funkcji Ω( µ , V ​​, T ) .

W przypadku, gdy więcej niż jeden rodzaj cząstek może zmieniać liczbę, wyrażenie prawdopodobieństwa uogólnia się do

${\ Displaystyle P = e ^ {\ Frac {\ Omega + \ mu _ {1} N_ {1} +\mu _{2}N_{2}+\ldokropki +\mu _{s}N_{s}-E}{kT}},}$

gdzie µ ₁ to potencjał chemiczny cząstek pierwszego rodzaju, N ₁ to liczba cząstek tego rodzaju w mikropaństwie, µ ₂ to potencjał chemiczny cząstek drugiego rodzaju itd. ( s to liczba różnych rodzaje cząstek). Te liczby cząstek stałych należy jednak dokładnie określić (zob. uwaga dotycząca zachowania liczby cząstek stałych poniżej).

Rozkład wielkiego zespołu kanonicznego jest nazywany przez niektórych autorów uogólnionym rozkładem Boltzmanna .

Wielkie zespoły są przydatne do opisywania układów, takich jak elektrony w przewodniku lub fotony we wnęce, gdzie kształt jest stały, ale energia i liczba cząstek mogą łatwo ulegać fluktuacjom w wyniku kontaktu ze zbiornikiem (np. ziemia lub ciemna powierzchnia , w takich przypadkach). Wielki zespół kanoniczny zapewnia naturalne ustawienie dla dokładnego wyprowadzenia statystyki Fermiego – Diraca lub statystyki Bosego – Einsteina dla układu nieoddziałujących cząstek kwantowych (patrz przykłady poniżej).

Uwaga dotycząca sformułowania

Alternatywne sformułowanie dla tego samego pojęcia zapisuje prawdopodobieństwo jako ${\ Displaystyle \ textstyle P = {\ Frac {1} {\ mathcal {Z}} } e ^ {(\ mu NE)/(kT)}}$ , używając funkcji wielkiego podziału ${\ Displaystyle \ textstyle {\ mathcal {Z}} = e ^ {- \ Omega /(kT)}}$ a nie wielki potencjał. Równania w tym artykule (pod względem wielkiego potencjału) można przekształcić w kategoriach funkcji wielkiego podziału za pomocą prostych manipulacji matematycznych.

Stosowalność

Wielki zespół kanoniczny to zespół opisujący możliwe stany układu izolowanego, który jest w równowadze termicznej i chemicznej ze zbiornikiem (wyprowadzenie przebiega wzdłuż linii analogicznych do wyprowadzenia w kąpieli cieplnej normalnego zespołu kanonicznego i można je znaleźć w Reif ). Wielki zespół kanoniczny odnosi się do systemów dowolnej wielkości, małych lub dużych; trzeba tylko założyć, że zbiornik, z którym się styka, jest znacznie większy (tj. przyjąć granicę makroskopową ).

Warunek, że system jest izolowany, jest konieczny, aby zapewnić, że ma on dobrze określone wielkości termodynamiczne i ewolucję. W praktyce jednak pożądane jest stosowanie wielkiego zespołu kanonicznego do opisu układów pozostających w bezpośrednim kontakcie ze zbiornikiem, ponieważ to właśnie kontakt zapewnia równowagę. Zastosowanie w tych przypadkach wielkiego zespołu kanonicznego jest zwykle uzasadnione albo 1) założeniem, że kontakt jest słaby, albo 2) włączeniem części połączenia złożowego do analizowanego układu, tak aby wpływ połączenia na rejon interes jest prawidłowo modelowany. Alternatywnie można zastosować podejścia teoretyczne do modelowania wpływu związku, uzyskując otwarty zespół statystyczny.

Innym przypadkiem, w którym pojawia się wielki zespół kanoniczny, jest rozważanie systemu, który jest duży i termodynamiczny (układ, który jest „w równowadze ze sobą”). Nawet jeśli dokładne warunki układu w rzeczywistości nie pozwalają na zmiany energii lub liczby cząstek, wielki zespół kanoniczny może być użyty do uproszczenia obliczeń niektórych właściwości termodynamicznych. Powodem tego jest to, że różne zespoły termodynamiczne ( mikrokanoniczny , kanoniczny ) stają się pod pewnymi względami równoważne wielkiemu zespołowi kanonicznemu, gdy system jest bardzo duży. Oczywiście w przypadku małych systemów różne zespoły nie są już równoważne nawet w średniej. W rezultacie wielki zespół kanoniczny może być bardzo niedokładny, gdy zastosuje się go do małych układów o stałej liczbie cząstek, takich jak jądra atomowe.

Nieruchomości

• Wyjątkowość : Wielki zespół kanoniczny jest jednoznacznie określony dla danego układu w danej temperaturze i przy danych potencjałach chemicznych i nie zależy od arbitralnych wyborów, takich jak wybór układu współrzędnych (mechanika klasyczna) lub podstawy (mechanika kwantowa). Wielki zespół kanoniczny jest jedynym zespołem ze stałymi $i$ V T , który odtwarza podstawową zależność termodynamiczną .
• Równowaga statystyczna (stan ustalony): Wielki zespół kanoniczny nie ewoluuje w czasie, pomimo faktu, że leżący u jego podstaw system jest w ciągłym ruchu. Rzeczywiście, zespół jest tylko funkcją zachowanych wielkości systemu (energia i liczba cząstek).
• Równowaga termiczna i chemiczna z innymi układami : Dwa układy, każdy opisany przez wielki zespół kanoniczny o równej temperaturze i potencjale chemicznym, doprowadzone do kontaktu termicznego i chemicznego pozostaną niezmienione, a powstały połączony układ zostanie opisany przez połączony wielki zespół kanoniczny te same temperatury i potencjały chemiczne.
• Maksymalna entropia : dla danych parametrów mechanicznych (ustalone $)$ ( zwana ” $E \ rangle}$ dowolnego zespołu (tj. rozkładu prawdopodobieństwa z samym itd . $Displaystyle \$ langle
• Minimalny potencjał wielki : Dla danych parametrów mechanicznych (ustalone V ) i danych wartości T , µ ₁ , …, µ _s , średnia zespołowa ${ \displaystyle \left\langle E+kT\log P-\mu _{1}N_{1}-\ldots \mu _{s}N_{s}\right\rangle } jest najniższym możliwym zespołem$ .

Wielki potencjał, średnie zespołowe i dokładne różnice

Pochodne cząstkowe funkcji Ω( µ ₁ , …, µ _s , V , T ) dają ważne wielkości średnie wielkiego zespołu kanonicznego:

• ${\ Displaystyle \ langle N_ {1} \ rangle = - {\ Frac {\$

  Ω
• średnie ciśnienie
  ${\ Displaystyle \ langle p \ rangle = - {\ Frac {\ częściowe \ Omega} {\ częściowe V}}}$
• entropia Gibbsa S
  $\ Displaystyle S = -k \ langle \ log P \ rangle = - {\ Frac {\ częściowe \ Omega} {\ częściowe T}} ,}$
• a średnia
  ${\ Displaystyle \ langle E \ rangle = \ Omega + \ langle N_ {1} \ rangle \ mu _ {1} \ ldots + \ langle N_ {s} \ rangle \ mu _ {s} + ST.}$

Dokładna różniczka : Z powyższych wyrażeń widać, że funkcja Ω ma dokładną różniczkę

${\ Displaystyle d \ Omega = -SdT- \ langle N_ {1} \ rangle d \ mu _ {1} \ ldots - \ langle N_ {s} \ rangle d \ mu _ {s} - \ langle p \ rangle dV .}$

Pierwsza zasada termodynamiki : Podstawiając powyższą zależność za ⟨ E ⟩ do dokładnej różniczki Ω , otrzymuje się równanie podobne do pierwszej zasady termodynamiki , z wyjątkiem średnich znaków niektórych wielkości:

${\ Displaystyle d \ langle E \ rangle = TdS + \ mu _ {1} d \ langle N_ {1} \ rangle \ ldots + \ mu _ {s} d \ langle N_ {s} \ rangle - \ langle p \ rangle dV.}$

Fluktuacje termodynamiczne : Różnice w energii i liczbie cząstek są

${\ Displaystyle \ langle E ^ {2} \ rangle - \ langle E \ rangle ^ {2} = kT ^ {2} {\ Frac {\ częściowy \ langle E \ rangle} {\ częściowy T}} + kT \ mu _{1}{\frac {\częściowy \langle E\rangle}{\częściowy \mu _{1}}}+kT\mu _{2}{\frac {\częściowy \langle E\rangle }{\częściowy \mu _ {2}}}+\ldots ,}$

${\ Displaystyle \ langle N_ {1} ^ {2} \ rangle - \ langle N_ {1} \ rangle ^ {2} = kT {\ Frac {\ częściowe \ langle N_ {1} \ rangle} {\ częściowe \ mu _{1}}}.}$

Korelacje fluktuacji : Kowariancje liczby cząstek i energii są

${\ Displaystyle \ langle N_ {1} N_ {2} \ rangle - \ langle N_ {1} \ rangle \ langle N_ {2} \ rangle = kT {\ Frac {\ częściowe \ langle N_ {2} \ rangle}} \częściowy \mu _{1}}}=kT{\frac {\częściowy \langle N_{1}\rangle }{\częściowy \mu _{2}}}}.}$

${\ Displaystyle \ langle N_ {1} E \ rangle - \ langle N_ {1} \ rangle \ langle E \ rangle = kT {\ Frac {\ częściowy \ langle E\rangle }{\częściowy \mu _{1}}},}$

Przykładowe zespoły

Przydatność wielkiego zespołu kanonicznego ilustrują poniższe przykłady. W każdym przypadku wielki potencjał obliczany jest na podstawie zależności

${\ Displaystyle \ Omega = -kT \ ln \ lewo (\ suma _ {\ tekst {mikrostany}} e ^ {\ Frac {\ mu NE }{kT}}\prawo)}$

co jest wymagane, aby prawdopodobieństwa mikrostanów sumowały się do 1.

Statystyki cząstek nieoddziałujących

Bozony i fermiony (kwantowe)

W szczególnym przypadku układu kwantowego wielu nieoddziałujących cząstek termodynamika jest łatwa do obliczenia. Ponieważ cząstki nie oddziałują ze sobą, można obliczyć szereg stanów stacjonarnych pojedynczych cząstek , z których każdy reprezentuje rozdzielną część, którą można włączyć do całkowitego stanu kwantowego układu. Na razie nazwijmy te jednocząstkowe stany stacjonarne orbitalami ( aby uniknąć mylenia tych „stanów” z całkowitym stanem wielu ciał), z zastrzeżeniem, że każda możliwa wewnętrzna właściwość cząstki ( spin lub polaryzacja ) liczy się jako oddzielny orbital. Każdy orbital może być zajęty przez cząstkę (lub cząstki) lub może być pusty.

Ponieważ cząstki nie oddziałują na siebie, możemy przyjąć, że każdy orbital tworzy oddzielny układ termodynamiczny . Zatem każdy orbital sam w sobie jest wielkim zespołem kanonicznym, tak prostym, że jego statystyki można tutaj natychmiast wyprowadzić. się tylko na jednym orbicie oznaczonym i , całkowita energia mikrostanu N cząstek na tym orbicie będzie wynosić Nϵ _i , gdzie ϵ _i jest charakterystycznym poziomem energii tego orbitalu. Wielki potencjał orbitalu jest określony przez jedną z dwóch postaci, w zależności od tego, czy orbital jest bozonowy, czy fermionowy:

• W przypadku fermionów zasada wykluczania Pauliego dopuszcza tylko dwa mikrostany dla orbitalu (zajęcie 0 lub 1), dając dwuczłonowy szereg

  ${\ Displaystyle {\ rozpocząć {wyrównane} \ Omega _ {i} & = - kT \ ln {\ Duży (} \ suma _ {N = 0} ^ {1} e ^ {\ Frac {N \ mu - N\epsilon _{i}}{kT}}{\Big )}\\&=-kT\ln {\Big (}1+e^{\frac {\mu -\epsilon _{i}}{kT }}{\Duży }}\end{wyrównany}}}$

• W przypadku bozonów N może być dowolną nieujemną liczbą całkowitą, a każda wartość N liczy się jako jeden mikrostan ze względu na nierozróżnialność cząstek , co prowadzi do szeregu geometrycznego :
  ${\ Displaystyle {\ rozpocząć {wyrównane} \ Omega _ {i} & = - kT \ ln {\ duży (} \ suma _ {N = 0} ^ {\ infty} e ^ {\ Frac {N \ mu -N \epsilon _{i}}{kT}}{\Big }}\\&=+kT\ln {\Big (}1-e^{\frac {\mu -\epsilon _{i}}{kT} }{\Duży )}.\end{wyrównany}}}$

W każdym przypadku wartość ${\ Displaystyle \ scriptstyle \ langle N_ {i} \ rangle = - {\ tfrac {\ częściowe \ Omega _ {i}} {\ częściowe \ mu} }}$ podaje średnią termodynamiczną liczbę cząstek na orbicie: rozkład Fermiego – Diraca dla fermionów i rozkład Bosego – Einsteina dla bozonów. Rozważając ponownie cały system, całkowity wielki potencjał można znaleźć, dodając Ω i _dla wszystkich orbitali.

Nieodróżnialne klasyczne cząstki

W mechanice klasycznej możliwe jest również rozważenie cząstek nierozróżnialnych (w rzeczywistości nierozróżnialność jest warunkiem wstępnym definiowania potencjału chemicznego w spójny sposób; wszystkie cząstki danego rodzaju muszą być wymienne). Ponownie rozważamy umieszczenie wielu cząstek tego samego rodzaju w tym samym mikrostanie przestrzeni fazowej pojedynczej cząstki, którą ponownie nazywamy „orbitalem”. Jednak w porównaniu z mechaniką kwantową przypadek klasyczny komplikuje fakt, że mikrostan w mechanice klasycznej nie odnosi się do pojedynczego punktu w przestrzeni fazowej, ale raczej do rozszerzonego obszaru w przestrzeni fazowej: jeden mikrostan zawiera nieskończoną liczbę stanów, wszystkie różne, ale o podobnym charakterze. W rezultacie, gdy wiele cząstek zostanie umieszczonych na tym samym orbicie, ogólny zbiór cząstek (w przestrzeni fazowej systemu) nie liczy się jako jeden cały mikrostan, ale raczej jako ułamek mikrostanu, ponieważ identycznych stanów (utworzonych przez permutację identycznych cząstek) nie należy przeliczać. Współczynnik korekcji przeliczenia jest silnią liczby cząstek.

Statystyki w tym przypadku mają postać wykładniczego szeregu potęgowego

${\ Displaystyle {\ rozpocząć {wyrównane} \ Omega _ {\ rm {orb}} & = - kT \ ln {\ duży (} \ suma _ {N = 0} ^ {\ infty }{\frac {1}{N!}}e^{\frac {N\mu -N\epsilon _{\rm {orb}}}{kT}}{\Big )}\\&=-kT \ln {\Big (}e^{e^{\frac {\mu -\epsilon _{\rm {orb}}}{kT}}}{\Big )}\\&=-kTe^{\frac {\mu -\epsilon _{\rm {kula}}}{kT}},\end{wyrównane}}}$

wartość ${\ Displaystyle \ scriptstyle \ langle N _ {\ rm {orb}} \ rangle = - {\ tfrac {\ częściowe \ Omega _ {\ rm {orb }}}{\partial \mu }}}$ odpowiadające statystyce Maxwella-Boltzmanna .

Jonizacja izolowanego atomu

Efekt jonizacji powierzchni w odparowanym atomie cezu w temperaturze 1500 K, obliczony przy użyciu metody opisanej w tej sekcji (z uwzględnieniem degeneracji ). oś Y: średnia liczba elektronów; atom jest neutralny, gdy ma 55 elektronów. Oś X: zmienna energii, która jest równa funkcji pracy powierzchni .

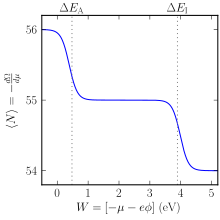
Wielki zespół kanoniczny może być użyty do przewidywania, czy atom woli być w stanie neutralnym, czy w stanie zjonizowanym. Atom może istnieć w stanie zjonizowanym z większą lub mniejszą liczbą elektronów w porównaniu do stanu neutralnego. Jak pokazano poniżej, stany zjonizowane mogą być preferowane termodynamicznie w zależności od środowiska. Rozważmy uproszczony model, w którym atom może znajdować się w stanie obojętnym lub w jednym z dwóch stanów zjonizowanych (szczegółowe obliczenia obejmują również współczynniki degeneracji stanów):

• stan neutralny pod względem ładunku, z N ₀ elektronami i energią E ₀ .
• stan utleniony ( ₀ N − 1 elektronów) o energii ₀ E + Δ E _I + qϕ
• stan zredukowany ( ₀ N + 1 elektrony) o energii ₀ E − Δ E _A − qϕ

Tutaj Δ E _I i Δ EA oznaczają odpowiednio _powinowactwo energię jonizacji atomu i elektronowe ; ϕ to lokalny potencjał elektrostatyczny w próżni w pobliżu atomu, a − q to ładunek elektronu .

Wielki potencjał w tym przypadku jest więc określony przez

${\ Displaystyle {\ rozpocząć {wyrównane} \ Omega & = - kT \ ln {\ duży (} e ^ {\ Frac {\ mu N_ {0} -E_ {0}} {kT}} + e ^ {\ frac {\mu N_{0}-\mu -E_{0}-\Delta E_{\rm {I}}-q\phi }{kT}}+e^{\frac {\mu N_{0}+\ mu -E_{0}+\Delta E_{\rm {A}}+q\phi }{kT}}{\Duży )}.\\&=E_{0}-\mu N_{0}-kT\ ln {\Big (}1+e^{\frac {-\mu -\Delta E_{\rm {I}}-q\phi }{kT}}+e^{\frac {\mu +\Delta E_ {\rm {A}}+q\phi }{kT}}{\Big )}.\\\end{wyrównane}}}$

Wielkość − qϕ − µ jest w tym przypadku krytyczna dla określenia równowagi między różnymi stanami. Ta wartość jest określana przez otoczenie wokół atomu.

Jeśli jeden z tych atomów zostanie umieszczony w skrzynce próżniowej, to − qϕ − µ = W , praca wyjścia materiału wyściełającego skrzynkę. Porównując tabele pracy pracy dla różnych materiałów stałych z tabelami powinowactwa elektronów i energii jonizacji dla rodzajów atomów, jasne jest, że wiele kombinacji skutkowałoby neutralnym atomem, jednak niektóre określone kombinacje skutkowałyby atomem preferującym stan zjonizowany: np. atom halogenu w iterbie pudełko lub atom cezu w pudełku wolframowym . W temperaturze pokojowej sytuacja ta nie jest stabilna, ponieważ atom ma tendencję do adsorpcji na odsłoniętej wyściółce pudełka zamiast swobodnego unoszenia się. Jednak w wysokich temperaturach atomy odparowują z powierzchni w postaci jonowej; ten spontaniczny jonizacji powierzchniowej został wykorzystany jako źródło jonów cezu .

W temperaturze pokojowej ten przykład znajduje zastosowanie w półprzewodnikach , gdzie jonizacja atomu domieszki jest dobrze opisana przez ten zespół. W półprzewodniku krawędź pasma przewodnictwa ϵ _C pełni rolę poziomu energii próżni (zastępując − qϕ ), a µ jest znane jako poziom Fermiego . Oczywiście energia jonizacji i powinowactwo elektronowe atomu domieszki są silnie modyfikowane w stosunku do ich wartości próżni. Typowa domieszka donorowa w krzemie, fosforze, ma Δ E _ja = 45 meV ; wartość ϵ _C − µ w samoistnym krzemie wynosi początkowo około 600 meV , gwarantując jonizację domieszki. Wartość ϵ _C − µ zależy jednak silnie od elektrostatyki, więc w pewnych warunkach możliwa jest dejonizacja domieszki.

Znaczenie potencjału chemicznego, uogólniona „liczba cząstek”

Zobacz też: Potencjał chemiczny

Aby liczba cząstek miała powiązany potencjał chemiczny, musi być zachowana podczas wewnętrznej dynamiki układu i może się zmieniać tylko wtedy, gdy układ wymienia cząstki z zewnętrznym zbiornikiem.

Jeśli cząstki mogą powstać z energii podczas dynamiki układu, to związany z nimi składnik µN nie może pojawić się w wyrażeniu prawdopodobieństwa dla wielkiego zespołu kanonicznego. W efekcie jest to to samo, co wymaganie, aby µ = 0 dla tego rodzaju cząstki. Tak jest w przypadku fotonów w czarnej wnęce , których liczba regularnie się zmienia w wyniku absorpcji i emisji na ścianach wnęki. (Z drugiej strony fotony w silnie odblaskowej wnęce mogą być zachowane i mogą mieć niezerową µ .)

W niektórych przypadkach liczba cząstek nie jest zachowana, a N reprezentuje bardziej abstrakcyjną ilość zachowaną:

• Reakcje chemiczne : Reakcje chemiczne mogą przekształcić jeden typ cząsteczki w inny; jeśli zachodzą reakcje, N _i muszą być określone w taki sposób, aby nie zmieniały się podczas reakcji chemicznej.
• Fizyka cząstek o wysokiej energii : Zwykłe cząstki mogą powstać z czystej energii, jeśli zostanie stworzona odpowiednia antycząstka . Jeśli tego rodzaju proces jest dozwolony, to ani liczba cząstek, ani antycząstki nie są zachowane. Zamiast tego N = (liczba cząstek - liczba antycząstek) jest zachowana. Wraz ze wzrostem energii cząstek jest więcej możliwości konwersji między typami cząstek, a więc jest mniej liczb, które są naprawdę zachowane. Przy najwyższych energiach jedynymi zachowanymi liczbami są ładunek elektryczny , słaba izospinowość i liczba barionowa − liczba leptonowa .

Z drugiej strony, w niektórych przypadkach jeden rodzaj cząstek może mieć wiele zachowanych liczb:

• Zamknięte przedziały : W systemie składającym się z wielu przedziałów, które współdzielą energię, ale nie dzielą cząstek, możliwe jest ustawienie potencjałów chemicznych oddzielnie dla każdego przedziału. Na przykład kondensator składa się z dwóch izolowanych przewodników i jest ładowany przez zastosowanie różnicy potencjału chemicznego elektronów .
• Powolna równowaga : W niektórych sytuacjach quasi-równowagi możliwe jest posiadanie dwóch różnych populacji tego samego rodzaju cząstek w tym samym miejscu, z których każda jest wewnętrznie zrównoważona, ale nie między sobą. Chociaż nie w ścisłej równowadze, przydatne może być nazwanie quasi-równowagowych potencjałów chemicznych, które mogą różnić się w różnych populacjach. Przykłady: ( fizyka półprzewodników ) odrębne poziomy quasi-Fermiego (potencjały chemiczne elektronów) w paśmie przewodnictwa i w paśmie walencyjnym ; ( spintronika ) różne potencjały chemiczne spin-up i spin-down; ( kriogenika ) różne potencjały chemiczne parawodoru i ortowodoru .

Precyzyjne wyrażenia dla zespołu

Dokładne wyrażenie matematyczne dla zespołów statystycznych ma różną postać w zależności od rodzaju rozważanej mechaniki (kwantowej lub klasycznej), ponieważ pojęcie „mikrostanu” jest znacznie różne. W mechanice kwantowej wielki zespół kanoniczny zapewnia prosty opis, ponieważ diagonalizacja zapewnia zestaw odrębnych mikrostanów układu, z których każdy ma dobrze zdefiniowaną energię i liczbę cząstek. Klasyczny przypadek mechaniczny jest bardziej złożony, ponieważ nie obejmuje stanów stacjonarnych, lecz całkę po kanonicznej przestrzeni fazowej .

Mechanika kwantowa

Dalsze informacje na temat reprezentacji zespołów w mechanice kwantowej: Zespół statystyczny (fizyka matematyczna)

Zespół statystyczny w mechanice kwantowej jest reprezentowany przez macierz gęstości , oznaczoną jako . $}$ } Wielki zespół kanoniczny to macierz gęstości

${\ Displaystyle {\ kapelusz {\ rho}} = \ exp {\ duży (} {\tfrac {1}{kT}}(\Omega +\mu _{1}{\hat {N}}_{1}+\ldots +\mu _{s}{\hat {N}}_{ s}-{\kapelusz {H}}){\duży )},}$

gdzie Ĥ jest operatorem całkowitej energii systemu ( hamiltonianem ), N̂ _{1 jest} operatorem całkowitej liczby cząstek w systemie dla cząstek typu 1, N̂ ₂ jest operatorem całkowitej liczby cząstek dla cząstek typu 2 i tak dalej. exp jest operatorem wykładniczym macierzy . Wielki potencjał Ω jest określony przez warunek normalizacji prawdopodobieństwa że ​​macierz gęstości ma ślad jeden, ${\ Displaystyle Tr {\ kapelusz {\ rho}} = 1}$ :

${\ Displaystyle e ^ {- {\ Frac {\ Omega} {kT}}} = \ nazwa operatora {Tr} \ exp {\ duży (}{\ tfrac {1} {kT}} (\ mu _ {1} \hat {N}}_{1}+\ldots +\mu _{s}{\kapelusz {N}}_{s}-{\kapelusz {H}}){\duży )}.}$

Zauważ, że dla wielkiego zespołu stany bazowe operatorów Ĥ , N̂ ₁ itd. to wszystkie stany z wieloma cząstkami w przestrzeni Focka , a macierz gęstości jest zdefiniowana na tej samej podstawie. Ponieważ energia i liczba cząstek są osobno zachowane, operatory te wzajemnie się dojeżdżają.

Wielki zespół kanoniczny można alternatywnie zapisać w prostej formie przy użyciu notacji nawiasowej , ponieważ możliwe jest (biorąc pod uwagę wzajemnie komutujący się charakter operatorów energii i liczby cząstek) znalezienie kompletnej bazy równoczesnych stanów własnych | ψ _ja ⟩ , indeksowane przez i , gdzie Ĥ | ψ _ja ⟩ = mi _ja | ψ _ja ⟩ , N̂ ₁ | ψ _ja ⟩ = N _{1, ja} | ψ _ja ⟩ i tak dalej. Biorąc pod uwagę taką podstawę własną, wielki zespół kanoniczny jest po prostu

${\ Displaystyle {\ kapelusz {\ rho}} = \ suma _ {i} e ^ {\ Frac {\ Omega + \ mu _ {1} N_ {1, i} + \ ldots + \ mu _ {s} N_ {s,i}-E_{i}}{kT}}|\psi _{i}\rangle \langle \psi _{i}|}$

${\ Displaystyle e ^ {- {\ Frac {\ Omega} {kT}}} = \ suma _ {i} e ^ {\ Frac {\ mu _ {1} N_ {1, i} + \ ldots + \ mu _{s}N_{s,i}-E_{i}}{kT}}.}$

gdzie suma jest nad całym zbiorem stanów ze stanem i o całkowitej energii E _{i ,} N _{1, i} cząstkach typu 1, N _{2, i} cząstkach typu 2 i tak dalej.

Klasyczny mechaniczny

Dalsze informacje na temat reprezentacji zespołów w mechanice klasycznej: Zespół statystyczny (fizyka matematyczna)

W mechanice klasycznej wielki zespół jest zamiast tego reprezentowany przez łączną funkcję gęstości prawdopodobieństwa zdefiniowaną w wielu przestrzeniach fazowych o różnych wymiarach, ρ ( N ₁ , … N _s , p ₁ , … p _n , q ₁ , … q _n ) , gdzie p q ₁ … p _{n 1} , … q n _, i są współrzędne kanoniczne (uogólnione pędy i uogólnione współrzędne) wewnętrznych stopni swobody układu. Wyrażenie dla wielkiego zespołu kanonicznego jest nieco delikatniejsze niż dla zespołu kanonicznego , ponieważ:

• Liczba cząstek, a tym samym liczba współrzędnych n, zmienia się w różnych przestrzeniach fazowych, a
• ważne jest, aby rozważyć, czy permutacja podobnych cząstek liczy się jako odrębny stan, czy nie.

W układzie cząstek liczba stopni swobody n zależy od liczby cząstek w sposób zależny od sytuacji fizycznej. Na przykład w trójwymiarowym gazie monoatomów n = 3 N , jednak w gazach molekularnych będą również obrotowe i wibracyjne stopnie swobody.

Funkcja gęstości prawdopodobieństwa dla wielkiego zespołu kanonicznego to:

${\ Displaystyle \ rho = {\ Frac {1} {h ^ {n} C}} e ^ {\ frac {\Omega +\mu _{1}N_{1}+\ldots +\mu _{s}N_{s}-E}{kT}},}$

Gdzie

• E jest energią układu, funkcją fazy ( N ₁ , … N _s , p ₁ , … p _n , q ₁ , … q _n ) ,
• h jest dowolną, ale z góry określoną stałą z jednostkami energia × czas , określającą zasięg jednego mikrostanu i zapewniającą prawidłowe wymiary ρ .
• C jest współczynnikiem korygującym przeliczenia (patrz poniżej), funkcją N ₁ , … N _s .

Ponownie, wartość Ω jest określana przez żądanie, aby ρ było znormalizowaną funkcją gęstości prawdopodobieństwa:

${\ Displaystyle e ^ {- {\ Frac {\ Omega} {kT}}} = \ suma _ {N_ {1} = 0} ^ {\ infty} \ ldots \ suma _ {N_ {s} = 0} ^ {\infty}\int \ldots \int {\frac {1}{h^{n}C}}e^{\frac {\mu _{1}N_{1}+\ldots +\mu _{s }N_{s}-E}{kT}}\,dp_{1}\ldots dq_{n}}$

Całka ta jest przejmowana przez całą dostępną przestrzeń fazową dla danej liczby cząstek.

Korekta przeliczenia

Dalsze informacje na temat przeliczania przestrzeni fazowej: zespół statystyczny (fizyka matematyczna)

Dobrze znanym problemem mechaniki statystycznej płynów (gazów, cieczy, plazmy) jest to, jak traktować cząstki, które mają podobny lub identyczny charakter: czy należy je uważać za rozróżnialne, czy nie? W równaniu ruchu systemu każda cząstka jest zawsze śledzona jako dająca się odróżnić jednostka, a jednak istnieją również ważne stany układu, w których pozycje każdej cząstki zostały po prostu zamienione: stany te są reprezentowane w różnych miejscach w przestrzeni fazowej, ale wydają się być równoważne.

Jeśli permutacje podobnych cząstek są uważane za odrębne stany, to powyższy czynnik C wynosi po prostu C = 1 . Z tego punktu widzenia zespoły obejmują każdy permutowany stan jako oddzielny mikrostan. Chociaż początkowo wydaje się to łagodne, prowadzi to do problemu bardzo nierozciągliwej entropii w zespole kanonicznym, znanego dziś jako paradoks Gibbsa . W wielkim zespole kanonicznym pojawia się kolejna logiczna niekonsekwencja: liczba rozróżnialnych permutacji zależy nie tylko od tego, ile cząstek znajduje się w układzie, ale także od tego, ile cząstek znajduje się w zbiorniku (ponieważ układ może wymieniać cząstki ze zbiornikiem). W tym przypadku entropia i potencjał chemiczny nie są ekstensywne, ale również źle zdefiniowane, w zależności od parametru (wielkości zbiornika), który powinien być nieistotny.

Aby rozwiązać te problemy, konieczne jest, aby wymiana dwóch podobnych cząstek (w systemie lub między systemem a zbiornikiem) nie była uważana za dającą odrębny stan systemu. Aby uwzględnić ten fakt, całki są nadal przenoszone przez pełną przestrzeń fazową, ale wynik jest dzielony przez

$\ Displaystyle C = N_ {1}! N_ {2}! \ ldots N_ {s}!,}$

czyli liczba różnych możliwych permutacji. Dzielenie przez C zgrabnie koryguje przeliczanie, które występuje w całce po całej przestrzeni fazowej.

Oczywiście możliwe jest włączenie rozróżnialnych typów cząstek do wielkiego zespołu kanonicznego - każdy rozróżnialny typ ${\ displaystyle i$$}$$przez$ oddzielny licznik cząstek $styl wyświetlania \mu _{i}}$ chemiczny . W rezultacie jedynym spójnym sposobem na włączenie „w pełni rozróżnialnych” cząstek do wielkiego zespołu kanonicznego jest rozważenie każdego możliwego do rozróżnienia typu tych cząstek i śledzenie każdego możliwego typu za pomocą oddzielnego licznika cząstek i oddzielnego potencjału chemicznego.