Wykres okresowy (krystalografia)

W przypadku innych zastosowań zobacz Wykres okresowy .
(Duża) komórka elementarna sieci kryształów diamentu ; kulki reprezentują węgla , a pałeczki reprezentują wiązania kowalencyjne
(Duża) komórka elementarna sieci kryształów kwarcu alfa ; czarne kulki to krzemu , a czerwone to tlen .

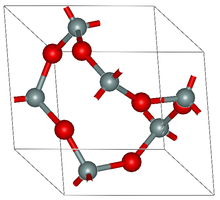
W krystalografii graf okresowy lub sieć krystaliczna jest trójwymiarowym grafem okresowym , tj. trójwymiarowym grafem euklidesowym , którego wierzchołki lub węzły są punktami w trójwymiarowej przestrzeni euklidesowej , a krawędzie (lub wiązania lub odstępy) są odcinkami linii łączące pary wierzchołków, okresowe w trzech liniowo niezależnych kierunkach osiowych. Zwykle przyjmuje się domniemane założenie, że zbiór wierzchołków jest jednostajnie dyskretny , tj. że istnieje ustalona minimalna odległość między dowolnymi dwoma wierzchołkami. Wierzchołki mogą reprezentować pozycje atomów lub kompleksów lub klastrów atomów, takich jak pojedyncze jony metali , molekularne bloki budulcowe lub drugorzędne jednostki budulcowe , podczas gdy każda krawędź reprezentuje wiązanie chemiczne lub ligand polimerowy .

Chociaż pojęcie wykresu okresowego lub sieci krystalicznej jest ostatecznie matematyczne (w rzeczywistości sieć krystaliczna to nic innego jak okresowa realizacja abelowego wykresu pokrywającego graf skończony) i jest ściśle związana z teselacją przestrzeni (lub plastra miodu ) w teorii polytopów i podobnych obszarów, większość współczesnych wysiłków w tej dziedzinie jest motywowana inżynierią kryształów i przewidywaniem (projektowaniem) , w tym szkieletami metaloorganicznymi (MOF) i zeolity .

Historia

Sieć krystaliczna to nieskończony molekularny model kryształu. Podobne modele istniały w starożytności , zwłaszcza teoria atomowa związana z Demokrytem , ​​którą krytykował Arystoteles , ponieważ taka teoria pociąga za sobą próżnię, którą według Arystotelesa natura brzydzi się . Nowoczesna teoria atomowa wywodzi się od Johannesa Keplera i jego pracy nad geometrycznymi problemami upakowania . Aż do XX wieku podobne do wykresów modele kryształów koncentrowały się na pozycjach składników (atomowych), a te modele sprzed XX wieku były przedmiotem dwóch kontrowersji w chemii i materiałoznawstwie.

Te dwie kontrowersje dotyczyły (1) kontrowersji wokół korpuskularnej teorii materii Roberta Boyle'a , według której wszystkie substancje materialne składają się z cząstek, oraz (2) kontrowersji dotyczących tego, czy kryształy są minerałami, czy też jakimś rodzajem zjawiska wegetatywnego. W XVIII wieku Kepler, Nicolas Steno , René Just Haüy i inni stopniowo powiązali upakowanie jednostek korpuskularnych typu Boyle'a w tablice z widocznym pojawieniem się w rezultacie struktur wielościennych przypominających kryształy. W XIX wieku wykonano znacznie więcej prac nad wielościanami a także struktury krystalicznej , zwłaszcza w wyprowadzaniu grup krystalograficznych w oparciu o założenie, że kryształ można uznać za regularny układ komórek elementarnych . Na początku XX wieku społeczność fizyków i chemików w dużej mierze akceptowała korpuskularną teorię materii Boyle'a — zwaną obecnie teorią atomową — a krystalografia rentgenowska była wykorzystywana do określania położenia składników atomowych lub molekularnych w komórkach elementarnych (przez początku XX wieku komórki elementarne uważano za mające znaczenie fizyczne).

Jednak pomimo rosnącego wykorzystania modeli molekularnych typu „stick-and-ball” , ostatnio popularne stało się stosowanie graficznych krawędzi lub segmentów linii do przedstawiania wiązań chemicznych w określonych kryształach, a także publikacje zachęcające do wysiłków w celu określenia graficznych struktur znanych kryształów, generować sieci krystaliczne z nieznanych jeszcze kryształów i syntetyzować kryształy tych nowych sieci krystalicznych. Jednoczesny wzrost zainteresowania tilingami i teselacjami , zwłaszcza modelującymi kwazikryształy , oraz rozwój nowoczesnej nanotechnologii , wszystko ułatwione przez dramatyczny wzrost mocy obliczeniowej, umożliwiło opracowanie algorytmów z geometrii obliczeniowej do budowy i analizy sieci krystalicznych. W międzyczasie starożytne powiązania między modelami kryształów i teselacji rozszerzyły się o topologię algebraiczną . W społeczności integracji na bardzo dużą skalę (VLSI) istnieje również wątek zainteresowania wykorzystaniem tych sieci kryształów jako projektów obwodów.

Podstawowy preparat

Graf euklidesowy w przestrzeni trójwymiarowej to para ( V , E ), gdzie V to zbiór punktów (czasami nazywanych wierzchołkami lub węzłami), a E to zbiór krawędzi (czasami nazywanych wiązaniami lub odstępnikami), gdzie każda krawędź łączy dwa wierzchołki. W literaturze wielościennej i chemicznej istnieje tendencja do określania grafów geometrycznych jako sieci (w przeciwieństwie do sieci wielościennych ), a nomenklatura w literaturze chemicznej różni się od nomenklatury w teorii grafów.

Symetrie i okresowość

Symetria wykresu euklidesowego jest izometrią podstawowej przestrzeni euklidesowej, której ograniczeniem do wykresu jest automorfizm ; grupa symetrii wykresu euklidesowego jest grupą jego symetrii. Graf euklidesowy w trójwymiarowej przestrzeni euklidesowej jest okresowy, jeśli istnieją trzy liniowo niezależne translacje , których ograniczeniami dla sieci są symetrie sieci. Często (i zawsze, jeśli mamy do czynienia z siecią krystaliczną) sieć okresowa ma skończoną liczbę orbit, a zatem jest jednostajnie dyskretna w tym, że istnieje minimalna odległość między dowolnymi dwoma wierzchołkami.

Rezultatem jest trójwymiarowy wykres okresowy jako obiekt geometryczny.

Powstała sieć krystaliczna będzie indukować siatkę wektorów tak, że mając trzy wektory generujące siatkę, te trzy wektory będą wiązać komórkę elementarną , czyli równoległościan , który umieszczony w dowolnym miejscu w przestrzeni obejmie powtarzający się w przestrzeni fragment sieci kierunkach trzech osi.

Symetria i rodzaje wierzchołków i krawędzi

Dwa wierzchołki (lub krawędzie) wykresu okresowego są symetryczne, jeśli znajdują się na tej samej orbicie grupy symetrii grafu; innymi słowy, dwa wierzchołki (lub krawędzie) są symetryczne, jeśli istnieje symetria sieci, która przesuwa się jeden na drugi. W chemii istnieje tendencja do określania orbit wierzchołków lub krawędzi jako „rodzajów” wierzchołków lub krawędzi, z uznaniem, że z dowolnych dwóch wierzchołków lub dowolnych dwóch krawędzi (podobnie zorientowanych) tej samej orbity graf geometryczny „wygląda ten sam". Można zastosować skończone kolory wierzchołków i krawędzi (gdzie symetrie mają zachować kolory).

Grupa symetrii sieci krystalicznej będzie (grupą ograniczeń a) krystalograficznej grupy przestrzennej , a wiele najpowszechniejszych kryształów ma bardzo wysoką symetrię, tj. bardzo mało orbit. Sieć krystaliczna jest jednowęzłowa, jeśli ma jedną orbitę wierzchołka (gdyby wierzchołki były kolorowe , a symetrie zachowywały kolory, wymagałoby to, aby odpowiedni kryształ miał atomy jednego pierwiastka lub molekularne elementy budulcowe jednego związku - ale nie odwrotnie, na przykład możliwe jest posiadanie kryształu jednego elementu, ale z kilkoma orbitami wierzchołków). Kryształy z jednowęzłowymi sieciami kryształów obejmują sześcienny diament i niektóre reprezentacje kryształów kwarcu . Jednowęzłowość odpowiada izogonalności w geometrii i przechodniości wierzchołków w teorii grafów i daje przykłady struktur obiektywnych. Sieć krystaliczna jest binodalna, jeśli ma dwie orbity o wierzchołkach; kryształy z binodalnymi sieciami krystalicznymi obejmują boracyt i anataz . Jest przechodni przez krawędź lub izotoksalny , jeśli ma jedną orbitę krawędzi; kryształy z sieciami kryształów przechodzącymi przez krawędź obejmują boracyt, ale nie anataz - który ma dwie orbity krawędzi.

Geometria sieci krystalicznych

W geometrii sieci krystalicznych krawędzie można traktować jako odcinki linii. Na przykład w sieci krystalicznej zakłada się, że krawędzie nie „zderzają się” w tym sensie, że traktując je jako odcinki linii, nie przecinają się. Z sieci krystalicznych można wyprowadzić kilka konstrukcji wielościennych. Na przykład figurę wierzchołka można uzyskać, dzieląc każdą krawędź (traktowaną jako odcinek linii) przez wstawienie punktów podziału, a wtedy figura wierzchołka danego wierzchołka jest wypukłą otoczką sąsiednich punktów podziału (tj . wielościan których wierzchołkami są sąsiednie punkty podziału).

Inną konstrukcją wielościenną jest wyznaczenie sąsiedztwa wierzchołka w sieci krystalicznej. Jednym z zastosowań jest zdefiniowanie funkcji energii jako (prawdopodobnie ważonej) sumy kwadratów odległości od wierzchołków do ich sąsiadów, a w odniesieniu do tej funkcji energii sieć jest w równowadze (w odniesieniu do tej funkcji energii), jeśli każdy wierzchołek jest umieszczony w środku ciężkości swojego sąsiedztwa, jest podstawą programu identyfikacji sieci kryształów SYSTRE. (matematycy używają terminu „realizacje harmoniczne” zamiast „sieci kryształów w pozycjach równowagi”, ponieważ pozycje charakteryzują się dyskretnym równaniem Laplace'a; wprowadzili także pojęcie realizacji standardowych, które są specjalnymi realizacjami harmonicznymi charakteryzującymi się pewną zasadą minimum też; patrz). Niektóre sieci krystaliczne są izomorficzne z sieciami krystalicznymi w pozycjach równowagi, a ponieważ pozycja równowagi to a postaci normalnej problem izomorfizmu sieci krystalicznej (tj. zapytanie , czy dwie dane sieci krystaliczne są izomorficzne jako wykresy; nie mylić z izomorfizmem krystalicznym ) jest łatwo obliczany, mimo że jako subsumpcja problemu izomorfizmu grafowego jest najwyraźniej obliczeniowo ogólnie trudne.

Aktywne obszary projektowania kryształów za pomocą sieci kryształów

Przypuszcza się, że sieci krystaliczne mogą minimalizować entropię w następującym sensie. Załóżmy, że dany jest zespół jednorodnie dyskretnych grafów euklidesowych, które wypełniają przestrzeń, z wierzchołkami reprezentującymi atomy lub cząsteczkowe bloki budulcowe i z krawędziami reprezentującymi wiązania lub ligandy, rozciągającymi się przez całą przestrzeń, aby reprezentować bryłę. W przypadku niektórych ograniczeń może istnieć unikalny wykres euklidesowy, który minimalizuje rozsądnie określoną energię funkcji, a przypuszczenie jest takie, że ten wykres euklidesowy może być koniecznie okresowy. To pytanie jest nadal otwarte, ale niektórzy badacze obserwują sieci krystaliczne o wysokiej symetrii, które mają tendencję do dominacji obserwowanych grafów euklidesowych pochodzących z niektórych klas materiałów.

Historycznie rzecz biorąc, kryształy były opracowywane w drodze eksperymentów, obecnie sformalizowane jako chemia kombinatoryczna , ale jednym ze współczesnych dezyderatów jest synteza wcześniej zaprojektowanych materiałów, a jedną z propozycji jest projektowanie kryształów (projektami są sieci krystaliczne, być może reprezentowane jako jedna komórka elementarna kryształu net), a następnie zsyntetyzować je z projektu. Ten wysiłek, w tym, co Omar Yaghi określił jako chemię siatkową, przebiega na kilku frontach, od teoretycznego do syntezy wysoce porowatych kryształów.

Jednym z głównych problemów związanych z wyżarzaniem kryształów jest kontrolowanie składników, co może być trudne, jeśli składnikami są pojedyncze atomy, np. w zeolitach , które są typowo porowatymi kryształami składającymi się głównie z krzemu i tlenu oraz okazjonalnych zanieczyszczeń. Synteza konkretnego zeolitu de novo z nowatorskiej sieci krystalicznej pozostaje jednym z głównych celów współczesnych badań. Podobne wysiłki podejmuje się w przypadku siarczków i fosforanów . [ potrzebne źródło ]

Kontrola jest łatwiejsza do opanowania, jeśli składniki są cząsteczkami budulcowymi, tj. stabilnymi cząsteczkami, które można łatwo zmusić do złożenia zgodnie z ograniczeniami geometrycznymi. [ Potrzebne źródło ] Zazwyczaj, chociaż może istnieć wiele gatunków składników, istnieją dwie główne klasy: nieco zwarte i często wielościenne drugorzędne jednostki budowlane (SBU) oraz łączące lub łączące jednostki budowlane. Popularną klasą przykładów są szkielety metaloorganiczne (MOF), w których (klasycznie) drugorzędnymi jednostkami budulcowymi są jony metali lub skupiska jonów i łączące je jednostki budulcowe są organicznymi ligandami . Te SBU i ligandy można stosunkowo kontrolować, a niektóre nowe kryształy zostały zsyntetyzowane przy użyciu projektów nowych sieci. Wariantem organicznym są kowalencyjne struktury organiczne (COF), w których SBU mogą (ale niekoniecznie) same być organiczne. [ potrzebne źródło ] Większą kontrolę nad SBU i ligandami można dostrzec w fakcie, że chociaż nie zsyntetyzowano żadnych nowych zeolitów według projektu, zsyntetyzowano kilka MOF z sieci krystalicznych zaprojektowanych do syntezy zeolitów, takich jak zeolitowe struktury metaloorganiczne (Z- MOF) [ potrzebne źródło ] i zeolitowy szkielet imidazolowy (ZIF).

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Periodic_graph_(crystallography)&oldid=1082301819 ”