W teorii prawdopodobieństwa i statystyce złożone zmienne losowe stanowią uogólnienie zmiennych losowych o wartościach rzeczywistych na liczby zespolone , tj. możliwe wartości, jakie może przyjąć złożona zmienna losowa, są liczbami zespolonymi . Złożone zmienne losowe można zawsze rozpatrywać jako pary rzeczywistych zmiennych losowych: ich część rzeczywistą i urojoną. Zatem rozkład jednej złożonej zmiennej losowej można interpretować jako łączny rozkład dwóch rzeczywistych zmiennych losowych.
Niektóre koncepcje rzeczywistych zmiennych losowych można łatwo uogólnić na złożone zmienne losowe — np. definicja średniej złożonej zmiennej losowej. Inne koncepcje są specyficzne dla złożonych zmiennych losowych.
Zastosowania złożonych zmiennych losowych można znaleźć w cyfrowym przetwarzaniu sygnałów , kwadraturowej modulacji amplitudy i teorii informacji .
Definicja
Złożona
zmienna
→
_ _
_
_ Z \ dwukropek \ Omega \rightarrow \ mathbb {C}}
jest
displaystyle
do {
funkcją Z
:
losowa
w
przestrzeni
Ω \ _ tak, że zarówno jego część rzeczywista
ℜ
( Z )
{\ Displaystyle \ Re {(Z)}}
ℑ
( Z )
{\ Displaystyle \ Im {(Z) )}}
zmiennymi losowymi na
( Ω ,
fa
, P )
{\ Displaystyle (\ Omega, {\ mathcal {F}}, P)}
Przykłady
Prosty przykład
Rozważmy zmienną losową
zespolone z prawdopodobieństwami
w tabeli .
, która może
Prawdopodobieństwo
P ( z )
{\ Displaystyle P (z)}
Wartość
z
{\ displaystyle z}
1 4
{\ Displaystyle {\ Frac {1} {4}}}
1 + ja
{\ displaystyle 1 + ja}
1 4
{\ Displaystyle {\ Frac {1} {4}}}
1 - ja
{\ Displaystyle 1-i}
1 2
{\ Displaystyle {\ Frac {1} {2}}}
2
{\ displaystyle 2}
Oczekiwanie tej
mi [ Z ] =
1 4
( 1
ja ) +
1 4
( 1 - ja ) +
1 2
2 =
3 2
.
zmiennej
{\ Displaystyle \ operatorname {E} [Z] = {\ Frac {1} {4}} (1 + i) + {\ Frac {1} {4}} (1-i) + {\ Frac {1} {2}}2={\frac {3}{2}}.}
+
Równomierna dystrybucja
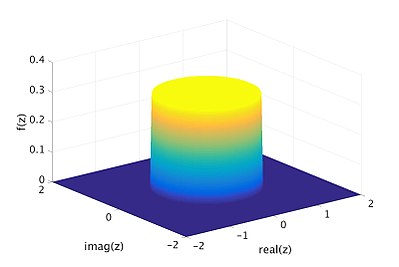
Innym przykładem złożonej zmiennej losowej jest rozkład równomierny po wypełnionym okręgu jednostkowym, czyli zbiór
{ z ∈
C
∣
|
z
|
≤ 1 }
{\ Displaystyle \ {z \ in \ mathbb {C} \ środek | z | \ równoważnik 1 \}
funkcję gęstości prawdopodobieństwa . Na poniższym rysunku funkcja gęstości jest pokazana jako żółty krążek i ciemnoniebieska podstawa.
Złożony rozkład normalny
W aplikacjach często spotyka się złożone zmienne losowe Gaussa. Są prostym uogólnieniem rzeczywistych zmiennych losowych Gaussa. Poniższy wykres przedstawia przykład rozkładu takiej zmiennej.
Dystrybuanta
Uogólnienie funkcji rozkładu skumulowanego z rzeczywistych na złożone zmienne losowe nie
.
jest oczywiste , ponieważ wyrażenia
postaci nie mają
w
P. ( ℜ
( Z )
≤ 1 , ℑ
( Z )
≤ 3 )
{\ Displaystyle P (\ Re {(Z)} \ równoważnik 1, \ Im {(Z)} \ równoważnik 3)}
łączny
ich
rozkład
rzeczywistych
i
0
złożonych zmiennych losowych
Dlatego
poprzez
rozkład _ części urojone:
fa
z
( z ) =
fa
ℜ
( z )
, ℑ
( z )
( ℜ
( z )
, ℑ
( z )
) = P ( ℜ
( z )
≤ ℜ
( z )
, ℑ
( Z )
≤ ℑ
( z )
)
{\ Displaystyle F_ {Z} (z) = F _ {\ Re {(Z)}, \ Im {(Z)}} (\ Re {(z)}, \ Im {(z)}) = P (\ Re {(Z)}\leq \Re {(z)},\Im {(Z)}\leq \Im {(z)})}
()
Funkcja gęstości prawdopodobieństwa
Funkcja gęstości prawdopodobieństwa złożonej zmiennej losowej jest zdefiniowana jako
fa
Z
( z ) =
fa
ℜ
( Z )
, ℑ
( Z )
( ℜ
( z )
, ℑ
( z )
)
{\ Displaystyle f_ {Z} (z) = f_{\Re {(Z)},\Im {(Z)}}(\Re {(z)},\Im {(z)})} , czyli wartość funkcji gęstości w
z ∈
C
{\ Displaystyle z \ in \ mathbb {C}}
( ℜ
( z )
, ℑ
( z )
)
{\ Displaystyle (\ Re {(z)}, \ Jestem {(z)})}
Równoważną definicję podaje
fa
Z
( z ) =
∂
2
∂ x ∂ y
P ( ℜ
( Z )
≤ x , ℑ
( Z )
≤ y )
{\ Displaystyle f_ {Z} (z) = {\ Frac {\ częściowy ^ {2}} {\ częściowy x \ częściowy y}} P (\ Re {(Z)} \ równoważnik x, \ Im {(Z)} \ równoważnik y)} gdzie x
ℜ ( z
) { \
displaystyle x=\Re {(z)}}
y
= ℑ
( z )
{\ Displaystyle y = \ Im {(z)}}
Podobnie jak w rzeczywistym przypadku funkcja gęstości może nie istnieć.
Oczekiwanie
Oczekiwanie złożonej zmiennej losowej definiuje się w oparciu o definicję oczekiwania rzeczywistej zmiennej losowej:
mi [ Z ] = mi [ ℜ
( Z )
] + ja mi [ ℑ
( Z )
]
{\ Displaystyle \ nazwa operatora {E} [Z] = \ nazwa operatora {E} [\ Re {(Z)}] +i\nazwa operatora {E} [\Im {(Z)}]}
()
Należy zauważyć, że oczekiwanie złożonej zmiennej losowej nie istnieje, jeśli
mi [ ℜ
( Z )
]
{\ displaystyle \ nazwa operatora {E} [\ Re {(Z)}]}
mi [ ℑ
( Z )
]
{\ displaystyle \operatorname {E} [\Im {(Z)}]}
złożona
]
mi [ Z
zmienna
ma
∬
do
z
to
Z
oczekiwanie
( z ) re x re y
{\ displaystyle \ nazwa operatora {E} [Z] = \ iint _ {\ mathbb {C}} z \ cdot f_ {Z} (z) \, dx \, dy}
,
=
⋅ fa
jest
przez
określone
zmienna
Z ] =
∑
Jeśli
∈
wówczas
funkcję
⋅
p
Z
( z )
{\ Displaystyle \ nazwa operatora {E} [Z] = \ suma _ {z \ in \ mathbb {Z}} z \ cdot p_ {Z} (z)}
[
złożona
masy
przez
z
Z z
mi
prawdopodobieństwa , oczekiwanie jest .
Nieruchomości Ilekroć istnieje oczekiwanie złożonej zmiennej losowej, przyjmując oczekiwanie i złożoną koniugację dojeżdżamy:
mi [ Z ]
¯
= mi [
Z ¯
] .
{\ Displaystyle {\ overline {\ nazwa operatora {E} [Z]}} = \ nazwa operatora {E} [{\ overline {Z}}].}
Operator wartości oczekiwanej jest liniowy w tym sensie, że
mi [ ⋅ ]
{\ displaystyle \ operatorname {E} [\ cdot]}
mi [ za Z + b W ] = za mi [ Z ] + b mi [ W ]
{\ displaystyle \ nazwa operatora {E} [aZ + bW] = a \ nazwa operatora {E} [Z] + b \ nazwa operatora {E} [W]}
dla
dowolnych
,
.
złożonych
niezależne
współczynników
nie
nawet
_ _
Wariancja i pseudowariancja
Wariancję definiuje się w kategoriach bezwzględnych kwadratów jako:
K
Z Z
= Var [ Z ] = mi
[
|
Z - mi [ Z ]
|
2
]
= mi [
|
Z
|
2
] −
|
E [ Z ]
|
2
{\ Displaystyle \ nazwa operatora {K} _ {ZZ} = \ nazwa operatora {Var} [Z] = \ nazwa operatora {E} \ lewo [\ lewo | Z- \ nazwa operatora {E} [Z] \ prawo | ^ {2 }\right]=\nazwa operatora {E} [|Z|^{2}]-\left|\nazwa operatora {E} [Z]\right|^{2}}
()
Nieruchomości Wariancja jest zawsze nieujemną liczbą rzeczywistą. Jest równa sumie wariancji części rzeczywistej i urojonej złożonej zmiennej losowej:
Var [ Z ] = Var [ ℜ
( Z )
] + Var [ ℑ
( Z )
] .
{\ Displaystyle \ nazwa operatora {Var} [Z] = \ nazwa operatora {Var} [\ Re {(Z)}] + \ nazwa operatora {Var} [\ Im {(Z)}].}
Wariancję kombinacji liniowej złożonych zmiennych losowych można obliczyć za pomocą następującego wzoru:
Var
[
∑
k = 1
N
za
k
Z
k
]
=
∑
ja = 1
N
∑
jot = 1
N
za
ja
jot
za
¯
.
Cov [
Z
ja
,
Z
jot
]
{\ Displaystyle \ operatorname {Var} \ lewo [\ suma _ {k = 1} ^ {N} a_ {k} Z_ {k} \ prawo] = \ suma _ {i = 1} ^ {N} \ suma _ {j=1}^{N}a_{i}{\overline {a_{j}}}\operatorname {Cov} [Z_{i},Z_{j}].}
Pseudo-wariancja
Pseudo -wariancja jest szczególnym przypadkiem pseudokowariancji i jest definiowana w kategoriach zwykłych zespolonych kwadratów , podanych wzorem:
jot
Z Z =
mi [ ( Z - mi [ Z ] )
2
]
= mi [ Z
2
]
- ( mi [ Z ] )
2
{
\ Displaystyle \ nazwa operatora {J} _ {ZZ} = \ nazwa operatora { E} [(Z-\nazwa operatora {E} [Z])^{2}]=\nazwa operatora {E} [Z^{2}]-(\nazwa operatora {E} [Z])^{2}}
()
pseudo
W przeciwieństwie
do
.
Macierz kowariancji części rzeczywistych i urojonych
W przypadku ogólnej złożonej zmiennej losowej para ma macierz kowariancji w postaci:
( ℜ
( Z )
, ℑ
( Z )
)
{\ Displaystyle (\ Re {(Z)}, \ Im {(Z)})}
[
Var [ ℜ
( Z )
]
Cov [ ℑ
( Z )
, ℜ
( Z )
]
Cov [ ℜ
( Z )
, ℑ
( Z )
]
Var [ ℑ
( Z )
]
]
{\ Displaystyle {\ początek {bmatrix} \ operatorname {Var} [\ Re {(Z)}] i \ operatorname {Cov} [\ Im {(Z)}, \ Re {(Z)}] \\\ nazwa operatora {Cov} [\Re {(Z)},\Im {(Z)}]&\operatorname {Var} [\Im {(Z)}]\end{bmatrix}}}
Macierz jest symetryczna, więc
Cov [ ℜ
( Z )
, ℑ
( Z )
] = Cov [ ℑ
( Z )
, ℜ
( Z )
]
{\ Displaystyle \ nazwa operatora {Cov} [\ Re {(Z)}, \Im {(Z)}]=\nazwa operatora {Cov} [\Im {(Z)},\Re {(Z)}]}
Jego elementy są równe:
Var [ ℜ
( Z )
] =
1 2
Re (
K
Z Z
+
jot
Z Z
)
Var [ ℑ
( Z )
] =
1 2
Re (
K
Z Z
-
jot
Z Z
)
Cov [ ℜ
( Z )
, ℑ
( Z )
] =
1 2
Im (
jot
Z Z
)
{\ Displaystyle {\ rozpocząć {wyrównane} i \ operatorname {Var} [\ Re {(Z)}] = {\ tfrac {1} {2}} \ nazwa operatora {Re} (\nazwa operatora {K} _{ZZ}+\nazwa operatora {J} _{ZZ})\\&\nazwa operatora {Var} [\Im {(Z)}]={\tfrac {1} 2}}\nazwa operatora {Re} (\nazwa operatora {K} _{ZZ}-\nazwa operatora {J} _{ZZ})\\&\nazwa operatora {Cov} [\Re {(Z)},\Im {( Z)}]={\tfrac {1}{2}}\nazwa operatora {Im} (\nazwa operatora {J} _{ZZ})\\\end{aligned}}}
Odwrotnie:
K
Z Z
= Var [ ℜ
( Z )
] + Var [ ℑ
( Z )
]
jot
Z Z
= Var [ ℜ
( Z )
] - Var [ ℑ
( Z )
] + ja 2 Cov [ ℜ
( Z )
,
ℑ
( Z )
]
{\ Displaystyle {\ początek {wyrównane} i \ nazwa operatora {K} _ {ZZ} = \ nazwa operatora {Var} [\ Re {(Z)}] + \ nazwa operatora {Var} [\ Im {( Z)}]\\&\nazwa operatora {J} _{ZZ}=\nazwa operatora {Var} [\Re {(Z)}]-\nazwa operatora {Var} [\Im {(Z)}]+i2\nazwa operatora {Cov} [\Re {(Z)},\Im {(Z)}]\end{aligned}}}
Kowariancja i pseudokowariancja
Kowariancję między dwiema
definiuje
złożonymi zmiennymi
jako
K
Z W
= Cov [ Z , W ] = mi [ ( Z - mi [ Z ] )
( W - mi [ W ] )
¯
] = mi [ Z
W ¯
] - mi [ Z ] mi [
W
¯
]
{\ Displaystyle \ nazwa operatora {K} _ {ZW} = \ nazwa operatora {Cov} [Z, W] = \ nazwa operatora {E} [(Z- \ nazwa operatora {E} [Z]) {\ overline {(W -\nazwa operatora {E} [W])}}]=\nazwa operatora {E} [Z{\overline {W}}]-\nazwa operatora {E} [Z]\nazwa operatora {E} [{\overline {W} }]}
()
Zwróć uwagę na złożoną koniugację drugiego czynnika w definicji.
( zwaną także wariancją komplementarną ):
jot
Z W
= Cov [ Z ,
W ¯
] = mi [ ( Z - mi [ Z ] ) ( W - mi [ W ] ) ] = mi [ Z W ] - mi [ Z ] mi [ W ]
{\ Displaystyle \ nazwa operatora {J} _ {ZW} = \ nazwa operatora {Cov} [Z, {\ overline {W}}] = \ nazwa operatora {E} [(Z- \ nazwa operatora {E} [Z]) (W -\nazwa operatora {E} [W])]=\nazwa operatora {E} [ZW]-\nazwa operatora {E} [Z]\nazwa operatora {E} [W]}
()
Statystyki drugiego rzędu w pełni charakteryzują się kowariancją i pseudokowariancją.
Nieruchomości Kowariancja ma następujące właściwości:
Cov [ Z , W ] =
Cov [ W , Z ]
¯
{\ Displaystyle \ operatorname {Cov} [Z, W] = {\ overline {\ operatorname {Cov} [W, Z]}}}
Cov [ α Z , W ] = α Cov [ Z , W ]
{\ Displaystyle \ operatorname {Cov} [\ alfa Z, W] = \ alfa \ operatorname {Cov} [Z, W]}
Cov [ Z , α W ] =
α ¯
Cov [ Z , W ]
{\ Displaystyle \ operatorname {Cov} [Z, \ alfa W] = {\ overline {\ alfa}} \ operatorname {Cov} [Z, W]}
Cov [
Z
1
+
Z
2
, W ] = Cov [
Z
1
, W ] + Cov [
Z
2
, W ]
{\ Displaystyle \ operatorname {Cov} [Z_ {1} + Z_ {2}, W] =\nazwa operatora {Cov} [Z_{1},W]+\nazwa operatora {Cov} [Z_{2},W]}
Cov [ Z ,
W
1
+
W
2
] = Cov [ Z ,
W
1
] + Cov [ Z ,
W
2
]
{\ Displaystyle \ operatorname {Cov} [Z, W_ {1} + W_ {2}] =\nazwa operatora {Cov} [Z,W_{1}]+\nazwa operatora {Cov} [Z,W_{2}]}
Cov [ Z , Z ] =
Var [ Z ]
{\ Displaystyle \ operatorname {Cov} [Z, Z] = {\ nazwa operatora {Var} [Z]}}
Nieskorelacja: dwie złożone zmienne losowe i
W.
operatora
nieskorelowanymi
\ nazwa
,
K
Z W
=
jot
Z W
= {\ displaystyle \ nazwa operatora {K} _ {ZW} =
0
{J} _ {ZW}=0}
nieskorelacja (teoria prawdopodobieństwa) ).
{ E }
Z
dwie złożone zmienne losowe i nazywane są ortogonalnymi, jeśli mi [ Z W
=
¯ ]
overline
0
0}
\ operatorname
[
\
{
=
{W}}]
Symetria kołowa
Symetria kołowa złożonych zmiennych losowych jest powszechnym założeniem stosowanym w dziedzinie komunikacji bezprzewodowej. Typowym przykładem kołowo-symetrycznej złożonej zmiennej losowej jest złożona zmienna losowa Gaussa z zerową średnią i zerową macierzą pseudokowariancji.
losowa
Złożona
determinizmu rozkład e
ϕ Z
symetryczna ,
jest
ja
dla
dowolnego
kołowo
_
jest
Z
{\ displaystyle Z}
Nieruchomości Z definicji zmienna losowa zespolona kołowo symetryczna ma
mi [ Z ] = mi [
mi
ja
ϕ
Z ] =
mi
ja
ϕ
mi [ Z ]
{\ Displaystyle \ nazwa operatora {E} [Z] = \ nazwa operatora {E} [e ^ {\ operatorname {i} \ phi }Z]=e^{\mathrm {i} \phi }\nazwa operatora {E} [Z]}
dla
dowolnego
_
.
Zatem oczekiwanie kołowo symetrycznej złożonej zmiennej losowej może wynosić tylko zero lub być nieokreślone.
Dodatkowo,
mi [ Z Z ] = mi [
mi
ja
ϕ
Z
mi
ja
ϕ
Z ] =
mi
2
ja ϕ
mi [ Z Z ]
{\ displaystyle \ nazwa operatora {E} [ZZ] = \ nazwa operatora {E} [e ^ {\mathrm {i} \phi }Ze^{\mathrm {i} \phi }Z]=e^{\mathrm {2} i\phi }\operatorname {E} [ZZ]}
dla
dowolnego
_
.
Zatem pseudowariancja kołowo symetrycznej złożonej zmiennej losowej może wynosić tylko zero.
Jeśli
i
mi
ϕ
rozłożona
displaystyle e ^ {\ operatorname {i} \ phi} Z}
Z
\
{
mają
[ - π
niezależnie od amplitudy
_
.
_
Właściwe złożone zmienne losowe
Pojęcie właściwych zmiennych losowych jest specyficzne dla złożonych zmiennych losowych i nie ma odpowiedniego pojęcia z rzeczywistymi zmiennymi losowymi.
Złożoną zmienną losową nazywa się właściwą, jeśli spełnione są wszystkie następujące trzy warunki:
Z
{\ displaystyle Z}
mi [ Z ] =
0
{\ Displaystyle \ nazwa operatora {E} [Z] = 0}
Var [ Z ] < ∞
{\ Displaystyle \ operatorname {Var} [Z] <\ infty}
mi [
Z
2
] =
0
{\ Displaystyle \ nazwa operatora {E} [Z ^ {2}] = 0}
Definicja ta jest równoważna następującym warunkom. Oznacza to, że złożona zmienna losowa jest właściwa wtedy i tylko wtedy, gdy:
mi [ Z ] =
0
{\ Displaystyle \ nazwa operatora {E} [Z] = 0}
mi [ ℜ
( Z )
2
] = mi [ ℑ
( Z )
2
] ≠ ∞
{\ Displaystyle \ nazwa operatora {E} [\ Re {(Z)} ^ {2}] = \ nazwa operatora {E} [\ Jestem {(Z)}^{2}]\neq \infty }
mi [ ℜ
( Z )
ℑ
( Z )
] =
0
{\ Displaystyle \ nazwa operatora {E} [\ Re {(Z)} \ Im {(Z)}] = 0}
Twierdzenie — Każda zmienna losowa zespolona kołowo symetryczna o skończonej wariancji jest właściwa.
W przypadku odpowiedniej złożonej zmiennej losowej macierz kowariancji pary ma następującą prostą postać
( ℜ
( Z )
, ℑ
( Z )
)
{\ Displaystyle (\ Re {(Z)}, \ Im {(Z)})}
[
1 2
Var [ Z ]
0
0
1 2
Var [ Z ]
]
{\ Displaystyle {\ początek {bmatrix} {\ Frac {1} {2}} \ operatorname {Var} [Z] i 0 \\ 0 i {\ Frac {1}{2}}\operatorname {Var} [Z]\end{bmatrix}}}
Tj:
Var [ ℜ
( Z )
] = Var [ ℑ
( Z )
] =
1 2
Var [ Z ]
Cov [ ℜ
( Z )
, ℑ
( Z )
] =
0
{\ Displaystyle {\ rozpocząć {wyrównane} i \ operatorname {Var} [\ Re {(Z)}] = \ operatorname {Var} [\ Im {(Z)}] = {\ tfrac {1} {2}} \operatorname {Var} [Z]\\&\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=0\\\end{aligned}}}
Nierówność Cauchy'ego-Schwarza
Cauchy'ego -Schwarza dla złożonych zmiennych losowych, którą można wyprowadzić za pomocą nierówności Trójkąta i nierówności Höldera , wynosi
|
mi
[
Z
W ¯
]
|
2
≤
|
E
[
|
Z
W ¯
|
]
|
2
≤ mi
[
|
Z
|
2
]
mi
[
|
W
|
2
]
{\ Displaystyle \ lewo | \ nazwa operatora {E} \ lewo [Z {\ overline {W}} \ prawo] \ prawo | ^ {2} \ równoważnik \ lewo | \ nazwa operatora {E} \ lewo [\ lewo | Z { \overline {W}}\right|\right]\right|^{2}\leq \operatorname {E} \left[|Z|^{2}\right]\operatorname {E} \left[|W| ^{2}\right]}
Funkcja charakterystyczna
Funkcja charakterystyczna złożonej zmiennej losowej to funkcja zdefiniowana przez
do
→ do
{
\ displaystyle \ mathbb {C} \ do \ mathbb {C}}
φ
Z
( ω ) = mi
[
mi
ja ℜ
(
ω ¯
Z )
]
= mi
[
mi
ja ( ℜ
( ω )
ℜ
( Z )
+ ℑ
( ω )
ℑ
( Z )
)
]
.
{\ Displaystyle \ Varphi _ {Z} (\ omega) = \ operatorname {E} \ lewo [e ^ {i \ Re {{\ overline {\ omega}} Z)}} \ prawo] = \ operatorname {E } \left[e^{i(\Re {(\omega )}\Re {(Z)}+\Im {(\omega )}\Im {(Z)})}\right].}
Zobacz też














![{\displaystyle \operatorname {E} [Z]={\frac {1}{4}}(1+i)+{\frac {1}{4}}(1-i)+{\frac {1}{2}}2={\frac {3}{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c524ba54cdf76d00057ff202c9ef13d276797808)




![{\displaystyle F_{Z}:\mathbb {C} \to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a49f4f55d06b18465dbc269884ebf7747b9156f3)







![{\displaystyle \operatorname {E} [Z]=\operatorname {E} [\Re {(Z)}]+i\operatorname {E} [\Im {(Z)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e1ff26c4d56190d3bcbbc0f5aaede2132ea4de)
![{\displaystyle \operatorname {E} [\Re {(Z)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e844e16f165052318326c84418f6f397eef22c61)
![{\displaystyle \operatorname {E} [\Im {(Z)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db17b20ce3199ef25f805f27c8473a08d3753378)
![{\displaystyle \operatorname {E} [Z]=\iint _{\mathbb {C} }z\cdot f_{Z}(z)\,dx\,dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce36d7e5aca36e4baed05d1ce7eb8be351a3da68)

![{\displaystyle \operatorname {E} [Z]=\sum _{z\in \mathbb {Z} }z\cdot p_{Z}(z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bd6feced28ac4cb07956d41e9b0476422f8b168)

![{\displaystyle {\overline {\operatorname {E} [Z]}}=\operatorname {E} [{\overline {Z}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0f389d24b8d094d5cbcfe0587f73462936d18ff)
![\operatorname {E}[\cdot ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a71518eb57ffaf54c0c31bf94de5ac9d7ab11a1)
![{\displaystyle \operatorname {E} [aZ+bW]=a\operatorname {E} [Z]+b\operatorname {E} [W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e642bbe3e97314e03a0804a0bcfeaaf4a49c7bc)


![{\displaystyle \operatorname {K} _{ZZ}=\operatorname {Var} [Z]=\operatorname {E} \left[\left|Z-\operatorname {E} [Z]\right|^{2}\right]=\operatorname {E} [|Z|^{2}]-\left|\operatorname {E} [Z]\right|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20d080a97d05f3891fad48566952956c8bc33616)
![{\displaystyle \operatorname {Var} [Z]=\operatorname {Var} [\Re {(Z)}]+\operatorname {Var} [\Im {(Z)}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/add16b3176754caaa4cf67a75a16b4ac92b34c76)
![{\displaystyle \operatorname {Var} \left[\sum _{k=1}^{N}a_{k}Z_{k}\right]=\sum _{i=1}^{N}\sum _{j=1}^{N}a_{i}{\overline {a_{j}}}\operatorname {Cov} [Z_{i},Z_{j}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f99e419701670b4886082740417b566f5c3f3123)
![{\displaystyle \operatorname {J} _{ZZ}=\operatorname {E} [(Z-\operatorname {E} [Z])^{2}]=\operatorname {E} [Z^{2}]-(\operatorname {E} [Z])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ff6bdd87afbafd84fa355854e5d4d7884b7cb5f)

![{\displaystyle {\begin{bmatrix}\operatorname {Var} [\Re {(Z)}]&\operatorname {Cov} [\Im {(Z)},\Re {(Z)}]\\\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]&\operatorname {Var} [\Im {(Z)}]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac330d152bea21f53db8f3ff194d894157b6fc3c)
![{\displaystyle \operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=\operatorname {Cov} [\Im {(Z)},\Re {(Z)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c2fd64c83c920bd9f44dfcb5281682245f7d103)
![{\displaystyle {\begin{aligned}&\operatorname {Var} [\Re {(Z)}]={\tfrac {1}{2}}\operatorname {Re} (\operatorname {K} _{ZZ}+\operatorname {J} _{ZZ})\\&\operatorname {Var} [\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Re} (\operatorname {K} _{ZZ}-\operatorname {J} _{ZZ})\\&\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Im} (\operatorname {J} _{ZZ})\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/660a39d44691cd1f64d313944c0046eeaa5fe2cc)
![{\displaystyle {\begin{aligned}&\operatorname {K} _{ZZ}=\operatorname {Var} [\Re {(Z)}]+\operatorname {Var} [\Im {(Z)}]\\&\operatorname {J} _{ZZ}=\operatorname {Var} [\Re {(Z)}]-\operatorname {Var} [\Im {(Z)}]+i2\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82090510b637bbd7629cffdef53b712e564ec908)

![{\displaystyle \operatorname {K} _{ZW}=\operatorname {Cov} [Z,W]=\operatorname {E} [(Z-\operatorname {E} [Z]){\overline {(W-\operatorname {E} [W])}}]=\operatorname {E} [Z{\overline {W}}]-\operatorname {E} [Z]\operatorname {E} [{\overline {W}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a961696e5eb2780adc679459b7cf2c5000dd1e)
![{\displaystyle \operatorname {J} _{ZW}=\operatorname {Cov} [Z,{\overline {W}}]=\operatorname {E} [(Z-\operatorname {E} [Z])(W-\operatorname {E} [W])]=\operatorname {E} [ZW]-\operatorname {E} [Z]\operatorname {E} [W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0850e20d08a280f61bd0e8db2c108656c09f163)
![{\displaystyle \operatorname {Cov} [Z,W]={\overline {\operatorname {Cov} [W,Z]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6c45f52a23a45d8c0489113054f2899fc7abe05)
![{\displaystyle \operatorname {Cov} [\alpha Z,W]=\alpha \operatorname {Cov} [Z,W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36d563b3f4a69e63da7c74774262faa56e9d8dbb)
![{\displaystyle \operatorname {Cov} [Z,\alpha W]={\overline {\alpha }}\operatorname {Cov} [Z,W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdae2df03771a6783a07fce94daafe717183d542)
![{\displaystyle \operatorname {Cov} [Z_{1}+Z_{2},W]=\operatorname {Cov} [Z_{1},W]+\operatorname {Cov} [Z_{2},W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58046998dba3171529973d2cea6df46bd55cd24b)
![{\displaystyle \operatorname {Cov} [Z,W_{1}+W_{2}]=\operatorname {Cov} [Z,W_{1}]+\operatorname {Cov} [Z,W_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21ba4eef59808fe6d651f74824fa7354b63de613)
![{\displaystyle \operatorname {Cov} [Z,Z]={\operatorname {Var} [Z]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d0dd5a038210af5d291b2baf8d6f5f4017130ba)

![{\displaystyle \operatorname {E} [Z{\overline {W}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9158c9d3364ee6a00a491d275b5aaa59fb06b08)
![{\displaystyle \phi \in [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd67c7af835707a32f70e8ceb8388953705d2ab3)

![{\displaystyle \operatorname {E} [Z]=\operatorname {E} [e^{\mathrm {i} \phi }Z]=e^{\mathrm {i} \phi }\operatorname {E} [Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a0c0eaaf719d6a7f539ee634a8ada78a25fb814)

![{\displaystyle \operatorname {E} [ZZ]=\operatorname {E} [e^{\mathrm {i} \phi }Ze^{\mathrm {i} \phi }Z]=e^{\mathrm {2} i\phi }\operatorname {E} [ZZ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d399819a5ae5dbfd8d504a1771a23da9424712fe)
![[-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)
![{\displaystyle \operatorname {E} [Z]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6c80bd7c75894b696a91f03059d601eed06827f)
![{\displaystyle \operatorname {Var} [Z]<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9598b3723f10a6af6b01d1a9e70dac49eaa054e)
![{\displaystyle \operatorname {E} [Z^{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0142e4405a348fd70966a8f62d4c260f5b30498)
![{\displaystyle \operatorname {E} [\Re {(Z)}^{2}]=\operatorname {E} [\Im {(Z)}^{2}]\neq \infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a24c7509a56aab23c94a541282cc12c0f2793e70)
![{\displaystyle \operatorname {E} [\Re {(Z)}\Im {(Z)}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38f594a6d61e9568109957798cff69ca1239516b)
![{\displaystyle {\begin{bmatrix}{\frac {1}{2}}\operatorname {Var} [Z]&0\\0&{\frac {1}{2}}\operatorname {Var} [Z]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/409bedd03d9fcbd63fb8d7338d6dc4ad4fe69e86)
![{\displaystyle {\begin{aligned}&\operatorname {Var} [\Re {(Z)}]=\operatorname {Var} [\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Var} [Z]\\&\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=0\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cc188b8b1273b1a3c41d381002ba1095ce961ec)
![{\displaystyle \left|\operatorname {E} \left[Z{\overline {W}}\right]\right|^{2}\leq \left|\operatorname {E} \left[\left|Z{\overline {W}}\right|\right]\right|^{2}\leq \operatorname {E} \left[|Z|^{2}\right]\operatorname {E} \left[|W|^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d22338d330f3e5c32c1fb25b14de2d80569cac86)

![{\displaystyle \varphi _{Z}(\omega )=\operatorname {E} \left[e^{i\Re {({\overline {\omega }}Z)}}\right]=\operatorname {E} \left[e^{i(\Re {(\omega )}\Re {(Z)}+\Im {(\omega )}\Im {(Z)})}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88cf0381ac2f47d34cdf5a23923e0699a8b6515d)