Zagrożona wartość entropiczna

W matematyce finansowej i optymalizacji stochastycznej koncepcja miary ryzyka służy do ilościowego określenia ryzyka związanego z losowym wynikiem lub pozycją ryzyka. Dotychczas zaproponowano wiele miar ryzyka, z których każda ma określone cechy. Entropiczna wartość zagrożona ( EVaR ) jest spójną miarą ryzyka wprowadzoną przez Ahmadi-Javida, która jest górną granicą wartości zagrożonej (VaR) i warunkowej wartości zagrożonej (CVaR), otrzymanej z nierówności Chernoffa . EVaR można również przedstawić za pomocą pojęcia entropii względnej . Ze względu na związek z VaR i względną entropią, ta miara ryzyka nazywana jest „entropiczną wartością ryzyka”. EVaR został opracowany w celu wyeliminowania pewnych nieefektywności obliczeniowej ^{[ wymagane wyjaśnienie ]} CVaR. Czerpiąc inspirację z podwójnej reprezentacji EVaR, Ahmadi-Javid opracował szeroką klasę spójnych miar ryzyka , zwanych g-entropicznymi miarami ryzyka . Zarówno CVaR, jak i EVaR są członkami tej klasy.

Definicja

Niech ${F}}, P)}$ $\ mathcal {F}}}$ będzie przestrzenią prawdopodobieństwa ze zbiorem wszystkich prostych zdarzeń, $}$ ${\ displaystyle {$ za ${\ Displaystyle \ sigma}$ $displaystyle$ podzbiorów ${\ Displaystyle \ Omega}$ i miary prawdopodobieństwa na ${\ mathcal {F}}}$ . Niech $będzie$ zmienną losową i $będzie$ zbiorem wszystkich mierzalnych funkcji Borela ${R}}$ X $: \ Omega \ do \$ $,$ którego funkcja generująca moment wszystkich $Z \ geq 0}$ . Entropiczna wartość zagrożona (EVaR) $}$ poziomem ufności $alpha$ jest następująco:

{\ Displaystyle {\ tekst {EVaR}} _ {1-\ alfa} (X): = \ inf _ {z> 0} \ lewo \ {z ^ {-1} \ ln \ lewo ({\ frac {M_ {X}(z)}{\alfa}}\prawo)\prawo\}.}

()

W finansach $używana$ losowa równaniu jest portfela .

Rozważ nierówność Chernoffa

{\ Displaystyle \ Pr (X \ geq a) \ równoważnik e ^ {- za} M_ {X} (z), \ quad \forall z>0.}

()

mi $Displaystyle e ^ {- za} M_ {X} (z) = \ alfa}$ \ dla za $\ Displaystyle a}$

{\ Displaystyle a_ {X} (\ alfa, z): = z ^ {-1} \ ln \ lewo ({\ Frac {M_ {X} (z)} {\ alfa}} \ prawo).}

Rozważając równanie ( 1 ), widzimy to

{\ Displaystyle {\ tekst {EVaR}} _ {1- \ alfa} (X): = \ inf _ {z> 0}\{a_{X}(\alfa ,z)\},}

co pokazuje związek między EVaR a nierównością Chernoffa. Warto zauważyć, że $jest$ miarą lub premią , która odpowiednio w finansach i ubezpieczeniach

Niech $} _ {M}}$ $których$ będzie zbiorem wszystkich mierzalnych funkcji Borela funkcja ${\ Displaystyle M_ {X} (z)}$ istnieje dla wszystkich ${\ Displaystyle Z}$ . Podwójna reprezentacja (lub solidna reprezentacja) EVaR jest następująca:

{\ Displaystyle {\ tekst {EVaR}} _ {1- \ alfa} (X) = \ sup _ {Q \ w \ im }(E_{Q}(X)),}

()

gdzie i $\$ $Displaystyle$ $miar$ prawdopodobieństwa na z ${\ Displaystyle \ Im = \ {Q \ ll P: D_ {KL} ( Q||P)\leq -\ln \alpha \}}$ . Zauważ to

{\ Displaystyle D_ {KL} (Q | | P): = \ int {\ Frac {dQ} dP}}\lewo(\ln {\frac {dQ}{dP}}\prawo)dP}

jest względną entropią w odniesieniu $.$ $_$ Kullbacka – Podwójna reprezentacja EVaR ujawnia powód jego nazewnictwa.

Nieruchomości

EVaR jest spójną miarą ryzyka.

Funkcja generująca moment $\$ być reprezentowana przez EVaR: dla wszystkich $mathbf {L} _ {M ^ {+}}}$ i ${\ displaystyle z> 0}$

{\ Displaystyle M_ {X} (z) = \ sup _ {0 <\ alfa \ równoważnik 1} \ {\ alfa \ exp (z {\ tekst {EVaR}} _ {1- \ alfa} (X)) \ }.}

()

dla ${\ Displaystyle X, Y \ in \ mathbf {L} _ {M}}$ , $= {\ tekst {EVaR}} _ {1- \ alfa} (Y)}$ ${\ Displaystyle {\ tekst {EVaR} } _ {1- \ alfa} (X$ ${\ Displaystyle \ alfa \ w] 0,1] }$ dla wszystkich $wszystkich$ i tylko wtedy, $} }$ ∈ $b$ .

Miarę ryzyka entropicznego z parametrem $za$ pomocą EVaR: dla wszystkich ${\ Displaystyle X \ in \ mathbf {L} _ {M ^ {+}} }$ i ${\ Displaystyle \ teta > 0}$

{\ Displaystyle \ teta ^ {-1} \ ln M_ {X} (\ teta) = a_ {X} (1, \ teta) = \ sup _ {0 <\ alfa \ równoważnik 1} \ {{\ tekst { EVaR}}_{1-\alpha}(X)+\theta ^{-1}\ln \alpha \}.}

()

EVaR z $\ displaystyle 1-\$ ufności $}$ ;

{\ Displaystyle {\ tekst {VaR}} (X) \ równoważnik {\ tekst {CVaR}} (X) \ równoważnik {\ tekst {EVaR}} (X).}

()

Następująca nierówność zachodzi dla EVAR:

{\ Displaystyle {\ tekst {E}} (X) \ równoważnik {\ tekst {EVaR}} _ {1- \ alfa} (X) \ leq {\text{esssup}}(X)}

()

gdzie

\ Displaystyle {\ tekst {E}} (X)}

{\ tekst {esssup}} (X)}

jest oczekiwaną wartością i jest esssup

Displaystyle

zasadnicze supremum X

{\ Displaystyle X}

, tj.

{\ Displaystyle \ inf _ {t \ in \ mathbb {R}} \ {t:

. Więc trzymaj

{\ Displaystyle {\ tekst {EVaR}} _ {0} (X) = {\ tekst {E}} (X)}

i

{\ Displaystyle \ lim _ {\ alfa \ do 0} {\ tekst {EVaR}} _ {1- \ alfa} (X) = {\ tekst {esssup}} (X)}

.

Przykłady

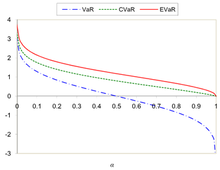
Porównanie VaR, CVaR i EVaR dla standardowego rozkładu normalnego

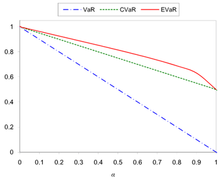
Porównanie VaR, CVaR i EVaR dla rozkładu jednorodnego w przedziale (0,1)

dla ${\ Displaystyle X \ sim N (\ mu, \ sigma ^ {2}),}$

{\ Displaystyle {\ tekst {EVaR}} _ {1- \ alfa} (X) = \ mu + \ sigma {\ sqrt {-2 \ ln \ alfa}}.}

()

dla ${\ Displaystyle X \ sim U (a, b)}$

{\ Displaystyle {\ tekst {EVaR}} _ {1- \ alfa} (X) = \ inf _ {t> 0} \ lewo \ lbrace t \ ln \ lewo (t {\ frac {e ^ {t ^ { -1}b}-e^{t^{-1}a}}{ba}}\right)-t\ln \alpha \right\rbrace .}

()

$0,1)}$ porównanie VaR, CVaR i EVaR dla i $U$ .

Optymalizacja

Niech $miarą$ ryzyka. Rozważ problem optymalizacji

{\ Displaystyle \ min _ {{\ pogrubiony symbol {w}} \ w {\ pogrubiony symbol {W}}} \ rho (G ({\ pogrubiony symbol {w}} , {\boldsymbol {\psi}}}),}

()

gdzie ${\ Displaystyle {\ boldsymbol {w}} \ in {\ boldsymbol {W}} \ subseteq \ mathbb {R} ^ {n}} jest -wymiarową rzeczywistą decyzją n {$ \ displaystyle $}$ wektor jest $-wymiarowym$ rzeczywistym wektorem losowym $o$ znanym rozkładzie prawdopodobieństwa funkcji $\ Displaystyle G({\boldsymbol {w}},.):\mathbb {R} ^{m}\to \mathbb {R} } jest$ mierzalną funkcją Borela dla wszystkich wartości ${\ Displaystyle {\ boldsymbol {w}} \ in {\ boldsymbol {W}}.}$ Jeśli ${\ Displaystyle \ rho = {\ tekst {EVaR}}},$ to problem optymalizacji ( 10 ) zamienia się w :

{\ Displaystyle \ min _ {{\ boldsymbol {w}} \ w {\ boldsymbol {W}}, t> 0} \ lewo \ {t \ ln M_ {G ({\ boldsymbol {w}}, {\ boldsymbol {\psi}})}(t^{-1})-t\ln \alpha \right\}.}

()

Niech $.$ wsparciem ${\ Displaystyle {\ boldsymbol {\ psi}}.}$ Jeśli ${\ Displaystyle G (., {\ boldsymbol {s}})}$ jest wypukła dla wszystkich ${\ Displaystyle {\ boldsymbol {s}}\in {\boldsymbol {S}}_{\boldsymbol {\psi}}}$ , to funkcja celu problemu ( 11 ) jest również wypukła. Jeśli ${\ Displaystyle G ({\ boldsymbol {w}}, {\ boldsymbol {\ psi}})}$ ma postać

{\ Displaystyle G ({\ boldsymbol {w}},{\boldsymbol {\psi}})=g_{0}({\boldsymbol {w}})+\sum _{i=1}^{m}g_{i}({\boldsymbol { w}})\psi _{i},\qquad g_{i}:\mathbb {R} ^{n}\to \mathbb {R} ,i=0,1,\ldots ,m,}

()

i są niezależnymi zmiennymi losowymi w $\ mathbf {L} _$ ${M}} ,$ a następnie ( 11 ) staje się

{\ Displaystyle \ min _ {{\ boldsymbol {w}} \ in {\ boldsymbol {W}}, t> 0} \ lewo \ lbrace g_ {0} ({\ boldsymbol {w}}) + t \ suma _ {i=1}^{m}\ln M_{g_{i}({\boldsymbol {w}})\psi _{i}}(t^{-1})-t\ln \alpha \right\ nawias klamrowy .}

()

który jest obliczeniowo traktowalny . Ale w tym przypadku, jeśli użyje się CVaR w problemie ( 10 ), wynikowy problem wygląda następująco:

{\ Displaystyle \ min _ {{\ boldsymbol {w}} \ in {\ boldsymbol {W}}, t \ in \ mathbb {R}} \ lewo \ lbrace t + {\ frac {1} {\ alfa}} \text{E}}\left[g_{0}({\boldsymbol {w}})+\sum _{i=1}^{m}g_{i}({\boldsymbol {w}})\psi _{i}-t\prawo]_{+}\prawo\rbrace .}

()

Można pokazać, że zwiększając wymiar $,$ ( 14 ) jest trudny obliczeniowo nawet w prostych przypadkach. $Załóżmy$ $różne$ że niezależnymi zmiennymi losowymi przyjmują wartości Dla ustalonych wartości i ${\ displaystyle mk}$ obliczania funkcji celu podanej w problemie ( ) jest rzędu m $mk}$ , podczas gdy m $k$ displaystyle czas obliczania funkcji celu problemu ( 14 ) jest uporządkowany ${\ displaystyle k ^ {m}}$ . Dla ilustracji załóżmy, że $sumowanie$ dwóch liczb zajmuje $-12$ sekund Do obliczenia funkcji celu problemu ( 14 ) potrzeba około $-$ ${\ displaystyle 10^{-10}}$ ocena funkcji celu problemu ( ) zajmuje około sekund. Pokazuje to, że formuła z EVaR przewyższa formułę z CVaR (więcej informacji znajduje się w artykule).

Uogólnienie (miary ryzyka g-entropowego)

Czerpiąc inspirację z podwójnej reprezentacji EVaR podanej w ( 3 ), można zdefiniować szeroką klasę spójnych miar ryzyka opartych na teorii informacji, które są wprowadzone w. Niech $funkcją$ wypukłą właściwą z $) = 0}$ $.$ i być liczbą nieujemną Miara $g }$ entropicznego z poziomem dywergencji jest zdefiniowana jako $sol$

{\ Displaystyle {\ tekst {ER}} _ {g, \ beta} (X): = \ sup _ {Q \ in \ Im} {\text{E}}_{Q}(X)}

()

w $_$ _ $g} (P, Q)}$ $P}$ { jest uogólnioną względną entropią względem $Displaystyle$ . Pierwotną reprezentację klasy -entropowych miar ryzyka można uzyskać w następujący sposób: sol {\ displaystyle $}$

{\ Displaystyle {\ tekst {ER}} _ {g, \beta }(X)=\inf _{t>0,\mu \in \mathbb {R}}\left\lbrace t\left[\mu +{\text{E}}_{P}\left( g^{*}\left({\frac {X}{t}}-\mu +\beta \right)\right)\right]\right\rbrace }

()

gdzie jest koniugatem ${\ displaystyle g ^ {*}}$ $∗ {\ displaystyle g }$ . rozważając

{\ Displaystyle g (x) = {\ rozpocząć {przypadki} x \ ln x & x> 0 \\ 0 i x = 0 \\ + \ infty & x < 0\end{przypadków}}}

()

sol ${\ Displaystyle g ^ {*} (x) = e ^ {x-1}}$ β $\ Displaystyle \ beta = - \ ln \ alfa}$ , można wydedukować formułę EVAR. CVaR jest również $ryzyka$ , którą można uzyskać z ( 16 ) ustawiając

{\ Displaystyle g (x) = {\ rozpocząć {przypadki} 0 i 0 \ równoważnik x \ równoważnik {\ Frac {1} {\ alfa}} \\ + \ infty &{\text{inaczej}}\end{przypadki}}}

()

z ${\ Displaystyle g ^ {*} (x) = {\ tfrac {1} {\ alfa}} \ max \ {0, x \}}$ i ${\ displaystyle \ beta = 0}$ (zobacz więcej szczegółów).

Aby uzyskać więcej wyników dotyczących -entropowych miar ryzyka, zobacz ${\ displaystyle g} .$

Zdyscyplinowane ramy programowania wypukłego

Ramy zdyscyplinowanego programowania wypukłego próbki EVaR zostały zaproponowane przez Cajasa i mają następującą postać:

{\ Displaystyle {\ rozpocząć {wyrównane}} {\ tekst {EVaR}} _ {\ alfa} (X) & = \ lewo \ {{\ rozpocząć {tablica} {ll} {\ underset {z, \,t,\,u}{\text{min}}}&t+z\ln \left({\frac {1}{\alpha T}}\right)\\{\text{st}}&z\ geq \sum _{j=1}^{T}u_{j}\\&(X_{j}-t,z,u_{j})\in K_{\text{exp}}\;\forall \ ;j=1,\ldots ,T\\\end{tablica}}\right.\end{wyrównane}}}

()

gdzie ${\ displaystyle z}$ , ${\ displaystyle t}$ i ${\ displaystyle u}$ są zmiennymi; ${\ Displaystyle K _ {\ tekst {exp}}}$ jest stożkiem wykładniczym; a $obserwacji$ . Jeśli zdefiniujemy $\$ wektor wag dla $w$ $}$ macierz $displaystyle$ i średni wektor aktywów, możemy postawić w { minimalizacja oczekiwanego EVaR przy danym poziomie oczekiwanego zwrotu z portfela $następujący$ sposób

{\ Displaystyle {\ rozpocząć {wyrównane} i {\ underset {w, \, z, \, t, \, u} {\ tekst {min}}} & & t + z \ ln \ left({\frac {1}{\alpha T}}\right)\\&{\text{st}}&&\mu w^{\tau}\geq {\bar {\mu}}\\&&&\ suma _{i=1}^{N}w_{i}=1\\&&&z\geq \sum _{j=1}^{T}u_{j}\\&&&(-r_{j}w^{ \tau }-t,z,u_{j})\in K_{\text{exp}}\;\forall \;j=1,\ldots ,T\\&&&w_{i}\geq 0\;\ ;\forall \;i=1,\ldots ,N\\\end{wyrównane}}}

()

Stosując ramy zdyscyplinowanego programowania wypukłego EVaR do niezłożonego skumulowanego rozkładu zysków, Cajas zaproponował entropiczny problem optymalizacji ryzyka ( EDaR ). Możemy postawić minimalizację oczekiwanego EDaR przy danym poziomie oczekiwanego zwrotu w następujący sposób: ${\ displaystyle {\ bar {\ mu}}}$

{\ Displaystyle {\ rozpocząć {wyrównane} i {\ underset {w, \, z, \, t, \, u, \, d} {\ tekst {min}}} & & t + z\ln \left({\frac {1}{\alpha T}}\right)\\&{\text{st}}&&\mu w^{\tau}\geq {\bar {\mu}} \\&&&\sum _{i=1}^{N}w_{i}=1\\&&&z\geq \sum _{j=1}^{T}u_{j}\\&&&(d_{j} -R_{j}w^{\tau }-t,z,u_{j})\in K_{\text{exp}}\;\forall \;j=1,\ldots ,T\\&&&d_{j }\geq R_{j}w^{\tau }\;\forall \;j=1,\ldots ,T\\&&&d_{j}\geq d_{j-1}\;\forall \;j=1 ,\ldots ,T\\&&&d_{j}\geq 0\;\forall \;j=1,\ldots ,T\\&&&d_{0}=0\\&&&w_{i}\geq 0\;;\; \forall \;i=1,\ldots ,N\\\end{wyrównane}}}

()

gdzie $jest$ zmienną reprezentującą niezłożone skumulowane zwroty z portfela, a $macierzą$ niezłożonych skumulowanych zwrotów z aktywów

W przypadku innych problemów, takich jak parytet ryzyka, maksymalizacja stosunku zwrotu do ryzyka lub ograniczenia maksymalnego poziomu ryzyka dla EVaR i EDaR, możesz zobaczyć więcej szczegółów.

Zaletą modelu EVaR i EDaR przy użyciu zdyscyplinowanej struktury programowania wypukłego jest to, że możemy używać oprogramowania takiego jak CVXPY lub MOSEK do modelowania problemów optymalizacji portfela. EVaR i EDaR są zaimplementowane w pakiecie Pythona Riskfolio-Lib.

Zobacz też