Zasada samokonsystencji Nowikowa

Zasada samokonsystencji Nowikowa , znana również jako hipoteza samokonsystencji Nowikowa i prawo zachowania historii Larry'ego Nivena , jest zasadą opracowaną przez rosyjskiego fizyka Igora Dmitrijewicza Nowikowa w połowie lat 80. Novikov zamierzał rozwiązać problem paradoksów w podróżach w czasie , co jest teoretycznie dozwolone w niektórych rozwiązaniach ogólnej teorii względności , które zawierają tak zwane zamknięte krzywe czasopodobne . Zasada głosi, że jeśli istnieje zdarzenie, które spowodowałoby paradoks lub jakąkolwiek „zmianę” w przeszłości, to prawdopodobieństwo tego zdarzenia wynosi zero. Nie byłoby więc możliwe tworzenie paradoksów czasowych .

Historia

Fizycy od dawna wiedzą, że niektóre rozwiązania ogólnej teorii względności zawierają zamknięte krzywe podobne do czasu — na przykład metryka Gödla . Nowikow omawiał możliwość istnienia zamkniętych krzywych podobnych do czasu (CTC) w książkach, które napisał w 1975 i 1983 roku, przedstawiając opinię, że dozwolone byłyby tylko samospójne podróże w przeszłość. W artykule Novikova i kilku innych z 1990 roku „ Problem Cauchy'ego w czasoprzestrzeniach z zamkniętymi krzywymi podobnymi do czasu” autorzy stwierdzają:

Jedyny rodzaj naruszenia przyczynowości, który autorzy uznaliby za niedopuszczalny, to ten zawarty w koncepcji science-fiction, polegającej na cofnięciu się w czasie i zabiciu młodszego siebie („zmiana przeszłości”). Kilka lat temu jeden z nas (Nowikow) pokrótce rozważał możliwość istnienia CTC i argumentował, że nie mogą one pociągać za sobą tego typu naruszenia przyczynowości: zdarzenia w CTC mają już gwarancję, że są spójne, argumentował Nowikow; wpływają na siebie nawzajem wokół zamkniętej krzywej w samoregulujący się, cykliczny, samospójny sposób. Inni autorzy niedawno doszli do tego samego punktu widzenia.

Ucieleśnimy ten punkt widzenia w zasadzie samozgodności, która mówi, że jedynymi rozwiązaniami praw fizyki, które mogą wystąpić lokalnie w rzeczywistym Wszechświecie, są te, które są globalnie samospójne. Zasada ta pozwala na zbudowanie lokalnego rozwiązania równań fizyki tylko wtedy, gdy to lokalne rozwiązanie można rozszerzyć na część (niekoniecznie unikalnego) globalnego rozwiązania, które jest dobrze zdefiniowane w nieosobliwych obszarach czasoprzestrzeni.

Wśród współautorów tego artykułu z 1990 roku byli Kip Thorne , Mike Morris i Ulvi Yurtsever, którzy w 1988 roku wzbudzili ponowne zainteresowanie tematem podróży w czasie w ogólnej teorii względności swoim artykułem „Tuleje czasoprzestrzenne, wehikuły czasu i słaba energia”. Warunek”, który pokazał, że nowe rozwiązanie ogólnej teorii względności znane jako przejezdny tunel czasoprzestrzenny mogło prowadzić do zamkniętych krzywych czasopodobnych iw przeciwieństwie do poprzednich rozwiązań zawierających CTC, nie wymagało nierealistycznych warunków dla wszechświata jako całości. Po dyskusjach z głównym autorem artykułu z 1990 roku, Johnem Friedmanem, przekonali się, że podróże w czasie nie muszą prowadzić do nierozwiązywalnych paradoksów, niezależnie od obiektu przesłanego przez tunel czasoprzestrzenny.

„Paradoks Polczyńskiego”
Rezolucja Echeverrii i Klinkhammera

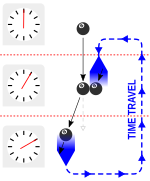
W odpowiedzi fizyk Joseph Polchinski napisał do nich list, w którym argumentował, że można uniknąć problemu wolnej woli, stosując potencjalnie paradoksalny eksperyment myślowy z kulą bilardową wysłaną w przeszłość przez tunel czasoprzestrzenny. W scenariuszu Polchinskiego kula bilardowa jest wystrzeliwana do tunelu czasoprzestrzennego pod takim kątem, że jeśli będzie dalej podążać swoją ścieżką, wyjdzie w przeszłości pod odpowiednim kątem, zderzając się ze swoim wcześniejszym ja, wytrącając go z toru i uniemożliwiając mu od wejścia do tunelu czasoprzestrzennego w pierwszej kolejności. Thorne odniósłby się do tego scenariusza jako „ Paradoks Polczyńskiego ” w 1994 roku.

Po rozważeniu scenariusza Fernando Echeverria i Gunnar Klinkhammer, dwaj studenci Caltech (gdzie wykładał Thorne), doszli do rozwiązania problemu, w którym udało się uniknąć wszelkich niespójności. W poprawionym scenariuszu piłka z przyszłości wyłania się pod innym kątem niż ten, który generuje paradoks, i zadaje młodszemu ja spojrzenie, zamiast całkowicie odrzucić ją od tunelu czasoprzestrzennego. Ten cios zmienia jego trajektorię o odpowiedni stopień, co oznacza, że ​​cofnie się w czasie pod kątem wymaganym do zadania młodszemu sobie niezbędnego ciosu. Echeverria i Klinkhammer faktycznie odkryli, że istnieje więcej niż jedno spójne rozwiązanie, z nieco innymi kątami uderzenia w każdej sytuacji. Późniejsza analiza przeprowadzona przez Thorne'a i Robert Forward zilustrował, że dla pewnych początkowych trajektorii kuli bilardowej może istnieć nieskończona liczba samospójnych rozwiązań.

Echeverria, Klinkhammer i Thorne opublikowali artykuł omawiający te wyniki w 1991 roku; ponadto poinformowali, że próbowali sprawdzić, czy mogą znaleźć jakiekolwiek warunki początkowe dla kuli bilardowej, dla których nie było samospójnych rozszerzeń, ale nie byli w stanie tego zrobić. Zatem jest prawdopodobne, że istnieją samospójne rozszerzenia dla każdej możliwej trajektorii początkowej, chociaż nie zostało to udowodnione. Dotyczy to tylko warunków początkowych poza obszarem czasoprzestrzeni naruszającym chronologię, który jest ograniczony horyzontem Cauchy'ego . Może to oznaczać, że zasada samospójności Novikova w rzeczywistości nie nakłada żadnych ograniczeń na systemy poza obszarem czasoprzestrzeni, w którym możliwe są podróże w czasie, tylko wewnątrz niego.

Nawet jeśli można znaleźć rozszerzenia samospójne dla dowolnych warunków początkowych poza horyzontem Cauchy'ego, odkrycie, że może istnieć wiele różnych rozszerzeń samospójnych dla tego samego warunku początkowego - w rzeczywistości Echeverria i in. znaleźli nieskończoną liczbę spójnych rozszerzeń dla każdej początkowej trajektorii, którą analizowali – może być postrzegane jako problematyczne, ponieważ klasycznie wydaje się, że nie ma sposobu, aby zdecydować, które rozszerzenie wybiorą prawa fizyki. Aby obejść tę trudność, Thorne i Klinkhammer przeanalizowali scenariusz kuli bilardowej za pomocą mechaniki kwantowej, wykonując sumę kwantowo-mechaniczną po historiach ( całka po trajektorii ) używając tylko spójnych rozszerzeń i stwierdził, że skutkowało to dobrze zdefiniowanym prawdopodobieństwem dla każdego spójnego rozszerzenia. Autorzy „Problemu Cauchy'ego w czasoprzestrzeniach z zamkniętymi krzywymi czasopodobnymi” piszą:

Najprostszym sposobem narzucenia zasady samozgodności w mechanice kwantowej (w klasycznej czasoprzestrzeni) jest sformułowanie sumy po historiach, w którym uwzględnia się wszystkie i tylko te historie, które są wewnętrznie spójne. Okazuje się, że przynajmniej formalnie (modulo takie kwestie jak zbieżność sumy), dla każdego wyboru początkowej, nierelatywistycznej funkcji falowej kuli bilardowej przed horyzontem Cauchy'ego , taka suma po historiach daje unikalne, samozgodne prawdopodobieństwa dla wyników wszystkich zestawów kolejnych pomiarów. ... Podejrzewamy, bardziej ogólnie, że dla dowolnego układu kwantowego w klasycznej czasoprzestrzeni tunelu czasoprzestrzennego ze stabilnym horyzontem Cauchy'ego suma wszystkich samozgodnych historii da unikalne, samozgodne prawdopodobieństwa dla wyników wszystkich zestawów pomiarów, które ktoś mógłby się zdecydować.

Założenia

Zasada spójności Novikova zakłada pewne warunki dotyczące tego, jaki rodzaj podróży w czasie jest możliwy. W szczególności zakłada, że ​​albo istnieje tylko jedna oś czasu , albo że żadne alternatywne osie czasu (takie jak te postulowane przez wieloświatową interpretację mechaniki kwantowej ) nie są dostępne.

Biorąc pod uwagę te założenia, ograniczenie, zgodnie z którym podróże w czasie nie mogą prowadzić do niespójnych wyników, można postrzegać jedynie jako tautologię , oczywistą prawdę, która nie może być fałszywa. Jednak zasada samokonsystencji Nowikowa ma wykraczać poza samo stwierdzenie, że historia musi być spójna, przyjmując dodatkowe nietrywialne założenie, że wszechświat podlega tym samym lokalnym prawom fizyki w sytuacjach związanych z podróżami w czasie, co w regionach przestrzeni - czas, którym brakuje zamkniętych krzywych czasopodobnych. Wyjaśnia to wspomniany wyżej „Problem Cauchy'ego w czasoprzestrzeniach z zamkniętymi krzywymi podobnymi do czasu”, gdzie autorzy piszą:

To, że zasada samozgodności nie jest całkowicie tautologiczna, staje się jasne, gdy rozważy się następującą alternatywę: prawa fizyki mogą dopuszczać CTC; a kiedy wystąpią CTC, mogą wywołać nowe rodzaje lokalnej fizyki, których wcześniej nie spotkaliśmy. ... Zasada samokonsekwencji ma na celu wykluczenie takiego zachowania. Upiera się, że lokalną fizyką rządzą te same rodzaje praw fizycznych, z którymi mamy do czynienia w przypadku braku CTC: prawa, które pociągają za sobą spójną, pojedynczą wartość dla pól. Zasadniczo zasada samospójności jest zasadą żadnej nowej fizyki. Jeśli ktoś jest skłonny od samego początku ignorować lub lekceważyć możliwość nowej fizyki, to uzna samospójność za trywialną zasadę.

Implikacje dla podróżników w czasie

Założenia zasady samospójności można rozszerzyć na hipotetyczne scenariusze z udziałem inteligentnych podróżników w czasie, a także nieinteligentnych obiektów, takich jak kule bilardowe. Autorzy „Problemu Cauchy'ego w czasoprzestrzeniach z zamkniętymi krzywymi podobnymi do czasu ” skomentowali tę kwestię w zakończeniu pracy, pisząc:

Jeśli CTC są dozwolone i jeśli powyższa wizja dostosowania się do nich fizyki teoretycznej okaże się mniej więcej poprawna, to co to będzie oznaczało dla filozoficznego pojęcia wolnej woli ludzi i innych istot inteligentnych? Z pewnością będzie to sugerować, że inteligentne istoty nie mogą zmienić przeszłości. Taka zmiana jest niezgodna z zasadą samospójności. W konsekwencji każda istota, która przeszła przez tunel czasoprzestrzenny i próbowała zmienić przeszłość, zostałaby powstrzymana przez prawo fizyczne przed dokonaniem zmiany; tj. „wolna wola” istoty byłaby ograniczona. Chociaż to ograniczenie ma charakter bardziej globalny niż ograniczenia wolnej woli, które wynikają ze standardowych, lokalnych praw fizyki, nie jest dla nas oczywiste, że to ograniczenie jest surowsze niż te, które nakładają standardowe prawa fizyczne.

Podobnie fizyk i astronom J. Craig Wheeler dochodzi do wniosku, że:

Zgodnie z hipotezą spójności wszelkie złożone interakcje międzyludzkie muszą przebiegać samoistnie, tak aby nie było paradoksu. Taka jest rezolucja. Oznacza to, jeśli wziąć to dosłownie, że jeśli istnieją wehikuły czasu, nie może być wolnej woli. Nie możesz zmusić się do zabicia młodszego siebie, jeśli cofniesz się w czasie. Można koegzystować, wychodzić na piwo, świętować razem urodziny, ale jakoś okoliczności podpowiadają, że nie można zachowywać się w sposób, który prowadzi do paradoksu w czasie. Nowikow wspiera ten punkt widzenia innym argumentem: fizyka już każdego dnia ogranicza twoją wolną wolę. Możesz zmusić się do latania lub przejścia przez betonową ścianę, ale grawitacja i fizyka materii skondensowanej podpowiadają, że nie możesz. Dlaczego, pyta Novikov, ograniczenie spójności nałożone na podróżnika w czasie jest inne?

Logika pętli czasowej

Główny artykuł: Pętla czasu

Logika pętli czasowej, ukuta przez robotyka i futurystę Hansa Moraveca , jest hipotetycznym systemem obliczeniowym, który wykorzystuje zasadę samokonsystencji Novikova do obliczania odpowiedzi znacznie szybciej niż jest to możliwe przy standardowym modelu złożoności obliczeniowej przy użyciu maszyn Turinga . W tym systemie komputer przesyła wynik obliczeń wstecz w czasie i opiera się na zasadzie samospójności, aby wymusić poprawność wysłanego wyniku, pod warunkiem, że maszyna może niezawodnie odbierać informacje z przyszłości i pod warunkiem, że algorytm i leżący u jego podstaw mechanizm są formalnie poprawne . Nieprawidłowy wynik lub brak wyniku może być nadal uzyskany, jeśli mechanizm lub algorytm podróży w czasie nie gwarantuje dokładności.

Prostym przykładem jest algorytm metody iteracyjnej . Morawiec stwierdza:

Stwórz skrzynkę obliczeniową, która przyjmuje dane wejściowe, które reprezentują przybliżone rozwiązanie jakiegoś problemu, i generuje wynik, który jest ulepszonym przybliżeniem. Konwencjonalnie zastosowałbyś takie obliczenie wielokrotnie skończoną liczbę razy, a następnie zadowalałbyś się lepszym, ale wciąż przybliżonym wynikiem. Przy odpowiednim ujemnym opóźnieniu możliwe jest coś innego: [...] wynik każdej iteracji funkcji jest cofany w czasie, aby służył jako „pierwsze” przybliżenie. Gdy tylko maszyna zostanie uruchomiona, tak zwany „punkt stały” F, wejście, które daje identyczne wyjście, zwykle sygnalizujące doskonałą odpowiedź, pojawia się (niezwykłym zbiegiem okoliczności!) natychmiast i stabilnie. [...] Jeśli iteracja nie jest zbieżna, to znaczy, jeśli F nie ma stałego punktu, wyjścia i wejścia komputera zostaną wyłączone lub zawisną w mało prawdopodobnym stanie pośrednim.

Obliczenia kwantowe z ujemnym opóźnieniem

Fizyk David Deutsch wykazał w 1991 roku, że ten model obliczeniowy może rozwiązywać problemy NP w czasie wielomianowym , a Scott Aaronson rozszerzył później ten wynik, aby pokazać, że model ten może być również użyty do rozwiązania PSPACE problemy w czasie wielomianowym. Deutsch pokazuje, że obliczenia kwantowe z ujemnym opóźnieniem — cofanie się w czasie — dają tylko rozwiązania spójne wewnętrznie, a obszar naruszający chronologię nakłada ograniczenia, które nie są widoczne w klasycznym rozumowaniu. Naukowcy opublikowali w 2014 roku symulację, w której twierdzą, że potwierdzili model Deutscha za pomocą fotonów. Jednak w artykule Tolksdorfa i Vercha wykazano, że warunek samokonsystencji Deutscha może być spełniony z dowolną precyzją w dowolnym układzie kwantowym opisanym zgodnie z relatywistyczną kwantową teorią pola nawet w czasoprzestrzeniach, które nie dopuszczają zamkniętych krzywych czasopodobnych, budząc wątpliwości, czy model Deutscha jest rzeczywiście charakterystyczny dla procesów kwantowych symulujących zamknięte krzywe czasopodobne w sensie ogólnej teorii względności . W późniejszym artykule ci sami autorzy pokazują, że warunek punktu stałego CTC Deutscha może być również spełniony w dowolnym systemie podlegającym prawom klasycznej mechaniki statystycznej , nawet jeśli nie jest zbudowany przez systemy kwantowe. Autorzy dochodzą do wniosku, że zatem warunek Deutscha nie jest specyficzny dla fizyki kwantowej ani nie zależy od kwantowej natury układu fizycznego, aby mógł zostać spełniony. W konsekwencji Tolksdorf i Verch argumentują, że warunek Deutscha nie jest wystarczająco konkretny, aby umożliwić stwierdzenie o scenariuszach podróży w czasie lub ich hipotetycznej realizacji przez fizykę kwantową.

Recepta Lloyda

Alternatywna propozycja została później przedstawiona przez Setha Lloyda, oparta na post-selekcji i całkach po trajektoriach. W szczególności całka po ścieżce jest po polach jednowartościowych, co prowadzi do samozgodnych historii.

W kulturze popularnej

  • The Final Countdown (1980): Film science-fiction o podróżach w czasie, w którym lotniskowiec USS Nimitz przechodzi przez tunel czasoprzestrzenny z powrotem do przedednia Pearl Harbor. Anomalia powraca i wysyła ją z powrotem do teraźniejszości, zanim będzie miała szansę wpłynąć na wynik.
  • Historia The Merchant and the Alchemist's Gate (2007) Teda Chianga bada wzajemne oddziaływanie między wolną wolą a konsekwentnymi podróżami w czasie
  • Steins; Gate (2009): Cytowane przez Makise Kurisu podczas jej prezentacji na temat podróży w czasie.
  • Harry Potter i metody racjonalności : W wykładzie Eliezera Yudkowsky'ego na temat racjonalności, ujętym w ramy fanfiction o Harrym Potterze, Harry próbuje użyć swojego Zmieniacza Czasu, aby wpłynąć na przeszłość i dochodzi do wniosku, że zasada samokonsekwencji Nowikowa ma zastosowanie.
  • Orthogonal : seria powieści science-fiction, która stosuje tę zasadę.
  • Seria Netflix Dark jest w dużej mierze oparta na założeniu, że możliwość podróży w czasie kusi bohaterów do próby zmiany przeszłości, co prowadzi ich tylko do spowodowania wydarzeń, którym starali się przede wszystkim zapobiec.
  • Outer Wilds (2019): gra wideo polegająca na podróżach w czasie, która nie jest zgodna z zasadą, powodując koniec gry, jeśli gracz eksperymentuje, aby to przetestować.

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Novikov_self-consistency_principle&oldid=1142353115 ”