epitrochoidalny

Epitrochoid z

R = 3

,

r = 1

i

d = 1/2

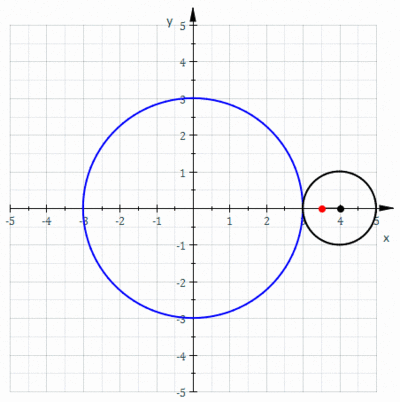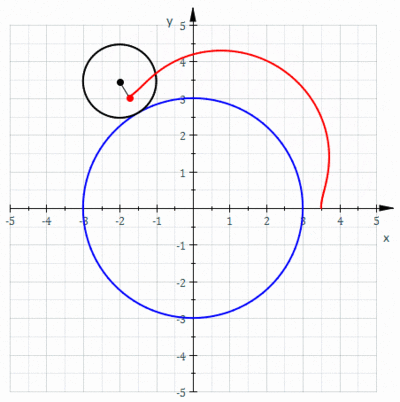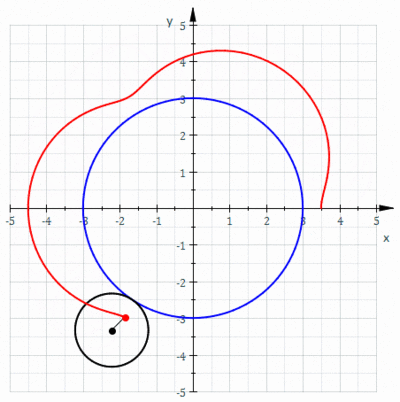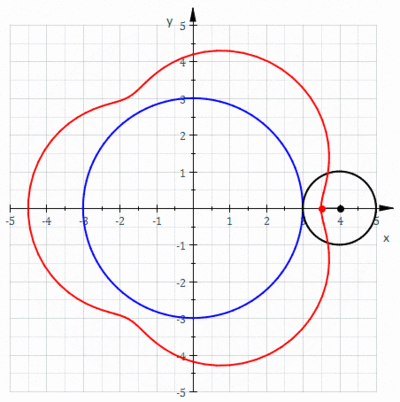
W geometrii epitrochoid ( / promieniu ɛ p ɪ t r ɒ k ɔɪ d / lub / d / ɛ p ɪ t r oʊ k to ) ɔɪ ruletka $śledzona$ przez punkt przymocowany do okręgu o r toczącego się po zewnętrznej stronie stałego okręgu o promieniu $R$ , którego punkt znajduje się w odległości $d$ od środka zewnętrznego okręgu.

Równania parametryczne dla epitrochoidy to

{\ displaystyle {\begin{wyrównane}&x(\theta )=(R+r)\cos \theta -d\cos \left({R+r \over r}\theta \right)\\&y(\theta)= (R+r)\sin \theta -d\sin \left({R+r \over r}\theta \right)\end{wyrównane}}}

Parametr $θ$ jest geometrycznie kątem biegunowym środka zewnętrznego koła. $_$ Jednak $θ$ kątem _

Szczególne przypadki obejmują limaçon z $R = r$ i epicykloidę z $d = r$ .

Klasyczna zabawka Spirograph śledzi krzywe epitrochoidalne i hipotrochoidalne .

Orbity planet w niegdyś popularnym geocentrycznym układzie Ptolemeusza to epitrochoidy (patrz deferent i epicykl ).

Orbita księżyca, gdy jest wyśrodkowana wokół słońca, jest zbliżona do epitrochoidy.

Komora spalania silnika Wankla jest epitrochoidą.

Zobacz też