Limaçon

Konstrukcja limaçon r = 2 + cos(π – θ) o początku współrzędnych biegunowych w ( x , y ) = ( 1 / 2 , 0)

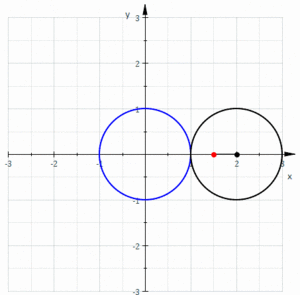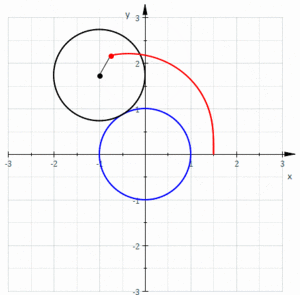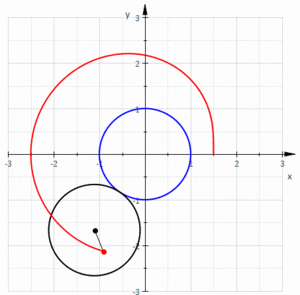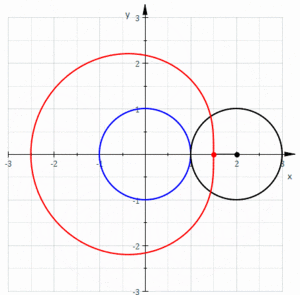
W geometrii limaçon lub limacon / toczy l ɪ m ə s ɒ n / , znany również jako limaçon Pascala lub Ślimaka Pascala , jest definiowany jako krzywa ruletki utworzona przez ścieżkę punktu przymocowanego do koła , gdy to koło się wokół zewnętrznej strony okręgu o równym promieniu. Można to również zdefiniować jako ruletkę, która powstaje, gdy koło toczy się po okręgu o połowie swojego promienia, tak że mniejszy okrąg znajduje się wewnątrz większego koła. Należą zatem do rodziny krzywych zwanych trochoidami centrowanymi ; dokładniej, są to epitrochoidy . Kardioida to szczególny przypadek, w którym punkt generujący ruletkę leży na toczącym się kole ; wynikowa krzywa ma wierzchołek .

W zależności od położenia punktu generującego krzywą, może mieć wewnętrzne i zewnętrzne pętle (stąd nazwa rodziny), może mieć kształt serca lub może być owalny.

Limaçon jest dwukolistą krzywą algebraiczną płaszczyzny wymiernej stopnia 4 .

Trzy limaçony: z wgłębieniami, z guzkiem (kardioida ) i zapętlone. Nie pokazano: wypukła limaçon

Historia

Najwcześniejsze formalne badania nad limaçonami przypisuje się na ogół Étienne Pascalowi , ojcu Blaise'a Pascala . Jednak niektóre wnikliwe badania na ich temat zostały podjęte wcześniej przez niemieckiego artystę renesansu Albrechta Dürera . Dürer's Underweysung der Messung (Instrukcja pomiaru) zawiera określone geometryczne metody produkcji limaçonów. Krzywa została nazwana przez Gillesa de Robervala, kiedy użył jej jako przykładu znajdowania linii stycznych.

równania

Równanie (do translacji i obrotu) limaçonu we współrzędnych biegunowych ma postać

${\ displaystyle r = b + a \ cos \ theta.}$

Można to przekonwertować na współrzędne kartezjańskie , mnożąc przez r (wprowadzając w ten sposób punkt na początku, który w niektórych przypadkach jest fałszywy) i podstawiając ${\ displaystyle r ^ {2} = x ^ {2 } + y ^ {2}}$ i ${\ Displaystyle r \ cos \ theta = x},$ aby uzyskać

${\ Displaystyle \ lewo (x ^ {2} + y ^ {2} -ax \ prawo) ^ {2} = b ^ {2} \ lewo (x ^ {2} + y ^ {2} \ prawo). }$

Stosując parametryczną formę konwersji polarnej na kartezjańską, mamy również

${\ Displaystyle x = (b + a \ cos \ teta) \ sałata \ teta = {a \over 2}+b\cos \theta +{a \over 2}\cos 2\theta ,}$

${\ Displaystyle y = (b + a \ cos \ teta) \ sin \ teta = b \ sin \ teta + {a \ ponad 2} \ grzech 2 \ teta;}$

podczas ustawiania

${\ Displaystyle z = x + iy = (b + a \ cos \ teta) (\ cos \ teta + i \sin \theta )}$

daje tę parametryzację jako krzywą na płaszczyźnie zespolonej :

${\ Displaystyle z = {a \ ponad 2} + być ^ {i \ teta} + {a \ ponad 2} e ^ {2i \ teta}.}$

Gdybyśmy przesunęli się w poziomie o ${\ textstyle - {\ Frac {1}{2}} a}$ , tj.

${\ Displaystyle z = być ^ {to} + {a \ ponad 2} e ^ {2it}}$ ,

zmienilibyśmy położenie początku układu współrzędnych, przechodząc do zwykłej postaci równania wyśrodkowanej trochoidy. Zwróć uwagę $na zmianę zmiennej niezależnej w tym momencie$ jasne, że nie używamy już domyślnej .

Przypadki specjalne

W szczególnym przypadku równanie biegunowe to ${\ displaystyle a = b}$

${\ Displaystyle r = b (1 + \ sałata \ teta) = 2b \ sałata ^ {2} {\ Frac {\ teta} {2} }}$

Lub

${\ Displaystyle R ^ {1 \ ponad 2} = (2b) ^ {1 \ ponad 2} \ sałata {\ Frac {\ teta} {2}} ,}$

co czyni go członkiem rodziny sinusoidalnych spirali krzywych. Ta krzywa jest kardioidalna .

W szczególnym przypadku wyśrodkowana postać trochoidalna równania staje się za $= 2b}$

${\ Displaystyle z = b \ lewo (e ^ {to} + e ^ {2 to} \ prawo) = być ^ {3 to \ ponad 2} \ lewo (e ^ {to \ ponad 2} + e ^ {- to \ ponad 2}\right)=2be^{3it \over 2}\cos {t \over 2},}$

lub we współrzędnych biegunowych,

${\ Displaystyle R = 2b \ sałata {\ teta \ ponad 3}}$

co czyni go członkiem różowej rodziny krzywych. Ta krzywa jest trisectrixem i jest czasami nazywana trisectrixem limaçon .

Formularz

Kiedy ${\ displaystyle b> a}$ limaçon jest prostą zamkniętą krzywą. Jednak początek spełnia równanie kartezjańskie podane powyżej, więc wykres tego równania ma anodę lub punkt izolowany.

Kiedy , $.$$gdy$ jest wypukły, krzywa wcięcie . $Displaystyle b$ za { \ 2a $jest$ punkt is a point of 0

Gdy $się$$w$ stosunku do $punkcie$ wcięcie staje się bardziej wyraźne, aż w staje się kardioidalna, a wcięcie się wierzchołkiem Dla $wewnętrznej pętli$ krzywa przecina się w początku jak ${\ displaystyle b}$ zbliża się do 0, pętla wypełnia zewnętrzną krzywą, aw granicy limaçon staje się kołem przebytym dwukrotnie.

Pomiar

${\ Displaystyle r = b + a \ cos \ theta}$ za sałata $+ { {a^{2}} \over 2}\right)\pi }$ π . Gdy ${\ displaystyle b <a}$ to dwukrotnie liczy obszar otoczony wewnętrzną pętlą. W tym przypadku krzywa przecina początek pod kątem ${\textstyle \pi \pm \arccos {b \over a}}$ , obszar objęty wewnętrzną pętlą to

${\ Displaystyle \ lewo (b ^ {2} + {{a ^ {2}} \ ponad 2} \ prawo)$

obszar objęty zewnętrzną pętlą wynosi

${\ Displaystyle \ lewo (b ^ {2} + {{a ^ {2}} \ ponad 2} \right)\left(\pi -\arccos {b \over a}\right)+{3 \over 2}b{\sqrt {a^{2}-b^{2}}},}$

a obszar między pętlami wynosi

${\ Displaystyle \ lewo (b ^ {2} + {{a ^ {2}} \ ponad 2} \ prawo) \ lewo (\ pi -2 \ arccos {b \ nad a} \ prawo) + 3b {\ sqrt {a^{2}-b^{2}}}.}$

Obwód limaçon jest określony przez całkowitą całkę eliptyczną drugiego rodzaju :

${\ Displaystyle 4 (a + b) E \ lewo ({{2 {\ sqrt {ab}}} \ nad a + b} \ prawo).}$

Stosunek do innych krzywych

• Niech będzie $punktem$ i będzie okręgiem, którego środkiem nie jest $P}$$displaystyle$ . $to limaçon$ obwiednia tych okręgów, których środek leży na $które$ przechodzą przez .

Limaçon — krzywa pedału koła

• Pedał koła to limaçon . W rzeczywistości pedał w odniesieniu do początku koła o promieniu $Displaystyle$ środku $(a, 0)}$ ma równanie biegunowe ${\ displaystyle r=b+a\cos \theta }$ .

• Odwrotność względem koła = $\ theta}$ jest

${\ Displaystyle r = {1 \ ponad {b + a \ cos \ theta}}},$

co jest równaniem a przekrój stożkowy z mimośrodem ${\ Displaystyle {\ tfrac {a} {b}}}$ i skup się na początku. Zatem limaçon można zdefiniować jako odwrotność stożka, w którym środek inwersji jest jednym z ognisk. Jeśli stożek jest parabolą, to odwrotność będzie kardioidą, jeśli stożek jest hiperbolą, to odpowiednia limakon będzie miała wewnętrzną pętlę, a jeśli stożek jest elipsą, to odpowiednia limakon nie będzie miała pętli.

• Muszla koła w stosunku do punktu na okręgu to limaçon.

• Szczególnym przypadkiem owalu kartezjańskiego jest limaçon.

Zobacz też

• Ruletka
• Wyśrodkowany trochoid
• Lista funkcji okresowych

Dalsza lektura

• Jane Grossman i Michaela Grossmana. „Dołek czy brak dołka” , The Two-Year College Mathematics Journal , styczeń 1982, strony 52–55.
• Howarda Antona. Rachunek różniczkowy , wydanie 2, strona 708, John Wiley & Sons, 1984.
• Howarda Antona. [1] s. 725 – 726.
• Howard Ewy. A Survey of Geometry , tom 2 (strony 51,56,273), Allyn and Bacon, 1965.

Linki zewnętrzne

• „Limacon of Pascal” w archiwum The MacTutor History of Mathematics
• „Limaçon” na stronie www.2dcurves.com
• „Limaçon of Pascal” w MathCurve
• „Limacon of Pascal” w Visual Dictionary of Special Plane Curves
• „Limacon of Pascal” na PlanetPTC (Mathcad)