Eksperyment Kennedy'ego-Thorndike'a

Rysunek 1. Eksperyment Kennedy'ego-Thorndike'a

Eksperyment Kennedy'ego-Thorndike'a , po raz pierwszy przeprowadzony w 1932 roku przez Roya J. Kennedy'ego i Edwarda M. Thorndike'a, jest zmodyfikowaną formą procedury eksperymentalnej Michelsona-Morleya , testującej szczególną teorię względności . Modyfikacja polega na tym, aby jedno ramię klasycznego aparatu Michelsona-Morleya (MM) było krótsze od drugiego. Podczas gdy eksperyment Michelsona-Morleya wykazał, że prędkość światła jest niezależna od orientacji aparatu , eksperyment Kennedy'ego-Thorndike'a wykazał, że jest również niezależny od prędkości urządzenia w różnych układach inercjalnych. Służył również jako test do pośredniej weryfikacji dylatacji czasu - podczas gdy negatywny wynik eksperymentu Michelsona-Morleya można wytłumaczyć samym skróceniem długości , negatywny wynik eksperymentu Kennedy'ego-Thorndike'a wymaga dylatacji czasu oprócz skrócenia długości, aby wyjaśnić, dlaczego żadne przesunięcia fazowe nie zostaną wykryte, gdy Ziemia porusza się wokół Słońca. Pierwsze bezpośrednie potwierdzenie dylatacji czasu uzyskano w eksperymencie Ivesa – Stilwella . Łącząc wyniki tych trzech eksperymentów, można wyprowadzić pełną transformację Lorentza .

Ulepszone warianty eksperymentu Kennedy'ego-Thorndike'a zostały przeprowadzone przy użyciu wnęk optycznych lub Lunar Laser Ranging . Aby zapoznać się z ogólnym przeglądem testów niezmienności Lorentza , zobacz Testy szczególnej teorii względności .

Eksperyment

Oryginalny eksperyment Michelsona-Morleya był przydatny tylko do testowania hipotezy skurczu Lorentza-FitzGeralda . Kennedy stworzył już kilka coraz bardziej wyrafinowanych wersji eksperymentu MM w latach dwudziestych XX wieku, kiedy wpadł na sposób testowania również dylatacji czasu . Własnymi słowami:

Zasada, na której opiera się ten eksperyment, polega na prostym twierdzeniu, że jeśli wiązkę jednorodnego światła podzielimy […] na dwie wiązki, które po przejściu dróg o różnych długościach ponownie się połączą, to względne fazy […] będą zależały [… ] na prędkość aparatu, chyba że częstotliwość światła zależy […] od prędkości w sposób wymagany przez teorię względności.

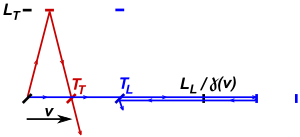
Nawiązując do rys. 1, kluczowe elementy optyczne zamontowano w komorze próżniowej V na podstawie z topionego kwarcu o wyjątkowo niskim współczynniku rozszerzalności cieplnej . Płaszcz wodny W utrzymywał temperaturę regulowaną z dokładnością do 0,001 °C. Monochromatyczne zielone światło ze źródła rtęci Hg przeszło przez polaryzacyjny pryzmat Nicol N przed wejściem do komory próżniowej i zostało rozszczepione przez rozdzielacz wiązki B ustawiony pod kątem Brewstera aby zapobiec niepożądanym odbiciom tylnej powierzchni. Dwie wiązki były skierowane w stronę dwóch zwierciadeł M1 _jak i M2 , które zostały ustawione w odległościach tak rozbieżnych, _długość to możliwe, biorąc pod uwagę koherencji linii rtęci 5461 Å (≈32 cm, dopuszczając różnicę w długości ramion Δ L ≈ 16 cm). Odbite promienie ponownie połączyły się, tworząc koliste prążki interferencyjne , które sfotografowano w punkcie P . Rozcięcie S umożliwił rejestrację wielokrotnych ekspozycji na średnicy pierścieni na jednej płycie fotograficznej w różnych porach dnia.

Dzięki temu, że jedno ramię eksperymentu byłoby znacznie krótsze od drugiego, zmiana prędkości Ziemi spowodowałaby zmiany w czasie przemieszczania się promieni świetlnych, z czego wynikałoby przesunięcie prążków, chyba że częstotliwość źródła światła zmieniłaby się na taką samą stopień. Aby ustalić, czy takie przesunięcie prążków miało miejsce, interferometr ustabilizowano, a wzory interferencyjne sfotografowano w celu późniejszego porównania. Testy trwały przez wiele miesięcy. Ponieważ nie stwierdzono znaczącego przesunięcia prążków (odpowiadającego prędkości 10 ± 10 km/s w granicach błędu), eksperymentatorzy doszli do wniosku, że dylatacja czasu zachodzi zgodnie z przewidywaniami szczególnej teorii względności.

Teoria

Podstawowa teoria eksperymentu

Rysunek 2. Ścieżka światła Kennedy'ego-Thorndike'a przy użyciu prostopadłych ramion

Chociaż skrócenie Lorentza-FitzGeralda (skurcz Lorentza) samo w sobie jest w stanie w pełni wyjaśnić zerowe wyniki eksperymentu Michelsona-Morleya, samo w sobie nie jest w stanie wyjaśnić zerowych wyników eksperymentu Kennedy'ego-Thorndike'a. Skrócenie Lorentza – FitzGeralda wyraża wzór:

${\ Displaystyle L = L_ {0} {\ sqrt {1-v ^ {2} / c ^ {2}}} = L_ {0} /{\gamma (v)}}$

Gdzie

${\ displaystyle L_ {0}}$ to właściwa długość (długość obiektu w jego układzie spoczynkowym), to długość obserwowana przez obserwatora

$displaystyle$ ruchu względnym względem obiektu, L {

$\$

$displaystyle v \,}$ to względna prędkość między obserwatorem a poruszającym się obiektem, tj. między hipotetycznym eterem a poruszającym się obiektem

$}$ prędkość światła do {\ displaystyle c \ ,

a czynnik Lorentza jest zdefiniowany jako

${\ Displaystyle \ gamma (v) \ równoważnik {\ Frac {1} {\ sqrt {1-v ^ {2} / c ^ {2}}}} \ }$ .

Ryc. 2 ilustruje aparat Kennedy'ego-Thorndike'a z prostopadłymi ramionami i zakłada ważność skurczu Lorentza. Jeśli aparat jest nieruchomy względem hipotetycznego eteru, różnica w czasie, w jakim światło przechodzi przez ramię podłużne i poprzeczne, jest dana wzorem:

${\ Displaystyle T_ {L} -T_ {T} = {\ Frac {2 (L_ {L} -L_ {T})} {c}}}$

Czas potrzebny światłu na przejście tam iz powrotem wzdłuż skróconej Lorentza długości ramienia podłużnego jest określony wzorem:

${\ Displaystyle T_ {L} = T_ {1} + T_ {2} = {\ Frac {L_ {L} / \ gamma (v)} {cv}} + {\ Frac {L_ {L} / \gamma (v)}{c+v}}={\frac {2L_{L}/\gamma (v)}{c}}{\frac {1}{1-{\frac {v^{2} }{c^{2}}}}}={\frac {2L_{L}\gamma (v)}{c}}}$

gdzie T ₁ to czas przemieszczania się w kierunku ruchu, T ₂ w kierunku przeciwnym, v to składowa prędkości względem świecącego eteru, c to prędkość światła, a L _L to długość podłużnego ramienia interferometru. Czas potrzebny światłu na przejście w poprzek i z powrotem ramienia poprzecznego jest określony wzorem:

${\ Displaystyle T_ {T} = {\ Frac {2L_ {T}} { \sqrt {c^{2}-v^{2}}}}={\frac {2L_{T}}{c}}{\frac {1}{\sqrt {1-{\frac {v^{ 2}}{c^{2}}}}}}={\frac {2L_{T}\gamma (v)}{c}}}$

Różnica w czasie, w jakim światło przechodzi przez ramię podłużne i poprzeczne, jest wyrażona wzorem:

${\ Displaystyle T_ {L} -T_ {T} = {\ Frac {2 (L_ {L} -L_ {T}) \ gamma (v)}{c}}}$

Ponieważ Δ L=c(T _L - T _T ) podane są następujące różnice długości ruchu (Δ LA _to początkowa różnica długości ruchu, a v _A to prędkość początkowa urządzenia, a Δ L _B i v _B po obrocie lub zmiana prędkości spowodowana własnym obrotem Ziemi lub jej obrotem wokół Słońca):

${\ Displaystyle \ Delta L_ {A} = {\ Frac {2 \ lewo (L_ {L} -L_ {T} \ prawej)} {\ sqrt {1-v_ {A} ^ {2} / c ^ {2 }}}},\qquad \Delta L_{B}={\frac {2\left(L_{L}-L_{T}\right)}{\sqrt {1-v_{B}^{2}/ c^{2}}}}}$ .

Aby otrzymać wynik ujemny, powinniśmy mieć Δ L _A −Δ L _B =0. Można jednak zauważyć, że oba wzory znoszą się tylko wtedy, gdy prędkości są takie same ( v _A = v _B ). Ale jeśli prędkości są różne, to Δ LA _B i Δ L _{. (Na} nie są już równe _{eksperyment Michelsona-Morleya nie mają wpływu zmiany prędkości ,} ponieważ różnica między LL i LT wynosi zero. Dlatego eksperyment MM sprawdza tylko, czy prędkość światła zależy od orientacji aparatu.) Ale w eksperymencie Kennedy'ego-Thorndike'a długości L _L i L _T są różne od samego początku, więc można również zmierzyć zależność prędkości światła od prędkości aparatu.

Zgodnie z poprzednim wzorem różnica długości podróży Δ L _A − Δ L _B i w konsekwencji oczekiwane przesunięcie prążków Δ N są wyrażone wzorem (λ jest długością fali):

${\ Displaystyle \ Delta N = {\ Frac {\ Delta L_ {A} - \ Delta L_ {B}} {\ lambda}} = {\ Frac {2 \ lewo (L_ {L} -L_ {T} \ prawo )}{\lambda }}\left({\frac {1}{\sqrt {1-v_{A}^{2}/c^{2}}}}-{\frac {1}{\sqrt { 1-v_{B}^{2}/c^{2}}}}\right)}$ .

Pomijając wielkości większe niż drugiego rzędu w v/c :

${\ Displaystyle \ około {\ Frac {L_ {L} -L_ {T}} {\ lambda}} \ lewo ({\ Frac {v_ {A}^{2}-v_{B}^{2}}{c^{2}}}\prawo)}$

Aby stała Δ N , tj. aby przesunięcie prążków było niezależne od prędkości lub orientacji aparatu, konieczne jest, aby częstotliwość, a tym samym długość fali λ, była modyfikowana przez współczynnik Lorentza. Tak jest w rzeczywistości, gdy bierze się pod uwagę wpływ dylatacji czasu na częstotliwość. Dlatego zarówno skrócenie długości, jak i dylatacja czasu są wymagane, aby wyjaśnić negatywny wynik eksperymentu Kennedy'ego-Thorndike'a.

Znaczenie dla teorii względności

Henri Poincaré i Albert Einstein wykazali, że transformacja Lorentza musi tworzyć grupę , aby spełnić zasadę względności (patrz Historia transformacji Lorentza ). Wymaga to, aby skrócenie długości i dylatacja czasu miały dokładne wartości relatywistyczne. Kennedy i Thorndike argumentowali teraz, że mogą wyprowadzić pełną transformację Lorentza wyłącznie z danych eksperymentalnych z eksperymentu Michelsona-Morleya i eksperymentu Kennedy'ego-Thorndike'a. Ale to nie jest do końca poprawne, ponieważ skrócenie długości i dylatacja czasu mające swoje dokładne wartości relatywistyczne są wystarczające, ale nie konieczne do wyjaśnienia obu eksperymentów. Dzieje się tak, ponieważ skrócenie długości wyłącznie w kierunku ruchu jest tylko jedną z możliwości wyjaśnienia eksperymentu Michelsona-Morleya. Ogólnie rzecz biorąc, jego wynik zerowy wymaga, aby stosunek między długościami poprzecznymi i podłużnymi odpowiada współczynnik Lorentza – który obejmuje nieskończenie wiele kombinacji zmian długości w kierunku poprzecznym i wzdłużnym. Wpływa to również na rolę dylatacji czasu w eksperymencie Kennedy'ego-Thorndike'a, ponieważ jej wartość zależy od wartości skrócenia długości zastosowanej w analizie eksperymentu. Dlatego konieczne jest rozważenie trzeciego eksperymentu, eksperymentu Ivesa-Stilwella , aby wyprowadzić transformację Lorentza z samych danych eksperymentalnych.

Dokładniej: W ramach teorii testu Robertsona-Mansouriego-Sexla do opisu eksperymentów można zastosować następujący schemat: α oznacza zmiany w czasie, β zmiany długości w kierunku ruchu, a δ zmiany długości prostopadłe do kierunku ruch. Eksperyment Michelsona-Morleya testuje związek między β i δ, podczas gdy eksperyment Kennedy'ego-Thorndike'a testuje związek między α i β. Tak więc α zależy od β, które samo zależy od δ, iw tych dwóch eksperymentach można zmierzyć tylko kombinacje tych wielkości, ale nie ich indywidualne wartości. Kolejny eksperyment jest konieczny, aby bezpośrednio zmierzyć wartość jednej z tych wielkości. W rzeczywistości osiągnięto to w eksperymencie Ivesa-Stilwella, w którym zmierzono, że α ma wartość przewidzianą przez relatywistyczną dylatację czasu. Połączenie tej wartości dla α z wynikiem zerowym Kennedy'ego-Thorndike'a pokazuje, że β koniecznie musi przyjąć wartość relatywistycznego skrócenia długości. A połączenie tej wartości dla β z wynikiem zerowym Michelsona-Morleya pokazuje, że δ musi wynosić zero. Tak więc niezbędne składniki transformacji Lorentza są dostarczane przez eksperyment, zgodnie z teoretycznymi wymaganiami teorii grup .

Ostatnie eksperymenty

Dalsze informacje: Nowoczesne wyszukiwania naruszenia Lorentza

Testy ubytkowe

Rycina 3. Uproszczony diagram Braxmaiera i in. 2002

W ostatnich latach eksperymenty Michelsona-Morleya oraz eksperymenty typu Kennedy-Thorndike zostały powtórzone ze zwiększoną precyzją przy użyciu laserów , maserów i kriogenicznych rezonatorów optycznych . Znacznie poprawiono granice zależności prędkości zgodnie z teorią testu Robertsona-Mansouri-Sexla (RMS), która wskazuje na zależność między dylatacją czasu a skróceniem długości. Na przykład oryginalny eksperyment Kennedy'ego-Thorndike'a ustalił granice zależności prędkości RMS na ~ 10-2 ^, ale obecne ograniczenia mieszczą się w ~ 10 zakres ^{−8 .}

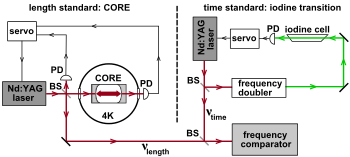
Ryc. 3 przedstawia uproszczony schematyczny diagram powtórzenia eksperymentu Kennedy'ego-Thorndike'a z 2002 roku przez Braxmaiera i in . Po lewej stronie fotodetektory (PD) monitorują rezonans standardu długości szafirowego kriogenicznego rezonatora optycznego (CORE) utrzymywanego w temperaturze ciekłego helu w celu ustabilizowania częstotliwości lasera Nd:YAG do 1064 nm. Po prawej linia absorbancji 532 nm niskociśnieniowego wzorca jodu jest używana jako wzorzec czasu do stabilizacji (podwojonej) częstotliwości drugiego lasera Nd:YAG.

Autor	Rok	Opis	Maksymalna zależność prędkości
Hilsa i Halla	1990	Porównanie częstotliwości optycznej wnęki Fabry'ego-Pérota z częstotliwością lasera stabilizowanego do linii odniesienia I2 .	${\ Displaystyle \ mniej 10 ^ {- 5}}$
Braxmaiera i in.	2002	I2 Porównanie częstotliwości kriogenicznego rezonatora optycznego ze standardem częstotliwości przy użyciu dwóch laserów Nd:YAG .
Wilk i in.	2003	Częstotliwość stacjonarnego kriogenicznego oscylatora mikrofalowego, składającego się z szafirowego kryształu pracującego w trybie szeptanej galerii , jest porównywana z maserem wodorowym , którego częstotliwość porównywano z atomowymi zegarami fontannowymi z cezu i rubidu . Poszukiwano zmian podczas obrotu Ziemi. Przeanalizowano dane z lat 2001–2002.	${\ Displaystyle \ mniej 10 ^ {- 7}}$
Wilk i in.	2004	Patrz Wilk i in. (2003). Zaimplementowano aktywną kontrolę temperatury. Przeanalizowano dane z lat 2002–2003.
Tobar i in.	2009	Patrz Wilk i in. (2003). Dane z lat 2002–2008 przeanalizowano zarówno pod kątem wahań gwiazdowych, jak i rocznych.	${\ Displaystyle \ mniej 10 ^ {- 8}}$

Księżycowy zasięg lasera

Oprócz pomiarów naziemnych, eksperymenty Kennedy'ego-Thorndike'a przeprowadzili Müller & Soffel (1995) oraz Müller i in. (1999) używając Lunar Laser Ranging , w których odległość Ziemia-Księżyc jest oceniana z dokładnością do centymetrów. Jeśli istnieje preferowany układ odniesienia, a prędkość światła zależy od prędkości obserwatora, to anomalne oscylacje powinny być obserwowane w pomiarach odległości Ziemia-Księżyc. Ponieważ dylatacja czasu została już potwierdzona z dużą precyzją, obserwacja takich oscylacji wykazałaby zależność prędkości światła od prędkości obserwatora, a także kierunkową zależność skrócenia długości. Jednak w żadnym z badań nie zaobserwowano takich oscylacji, przy prędkości RMS ograniczonej do ~10 ⁻⁵ , porównywalne z granicami wyznaczonymi przez Hilsa i Halla (1990). Dlatego zarówno skrócenie długości, jak i dylatacja czasu muszą mieć wartości przewidziane przez teorię względności.