Dynamiczny prostokąt
Dynamiczny prostokąt to prostokątna, czworoboczna figura ( prostokąt ) o dynamicznej symetrii , co w tym przypadku oznacza, że współczynnik kształtu (szerokość podzielona przez wysokość) jest wartością wyróżniającą dynamiczną symetrię , system proporcji i naturalny projekt metodologia opisana w książkach Jaya Hambidge'a . Te dynamiczne prostokąty rozpoczynają się od kwadratu , który jest przedłużany (za pomocą szeregu łuków i punktów przecięcia) w celu uzyskania pożądanej figury, którą może być złoty prostokąt (1 : 1,618...), prostokąt 2:3, podwójny kwadrat (1:2) lub pierwiastek prostokątny (1: √ φ , 1: √ 2 , 1: √ 3 , 1: √ 5 itd.).
Prostokąty korzeni
Prostokąt pierwiastkowy to prostokąt , w którym stosunek dłuższego boku do krótszego jest pierwiastkiem kwadratowym liczby całkowitej , takiej jak √ 2 , √ 3 itd.
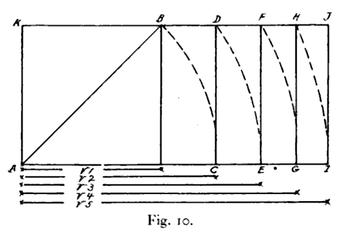
Prostokąt pierwiastkowy 2 (ACDK na ryc. 10) jest konstruowany przez wydłużenie dwóch przeciwległych boków kwadratu do długości przekątnej kwadratu. Prostokąt pierwiastkowy 3 jest konstruowany przez wydłużenie dwóch dłuższych boków prostokąta pierwiastkowego 2 do długości przekątnej prostokąta pierwiastkowego 2. Każdy kolejny prostokąt główny jest tworzony przez wydłużenie dłuższych boków prostokąta głównego, aby były równe długości przekątnej tego prostokąta.
Nieruchomości
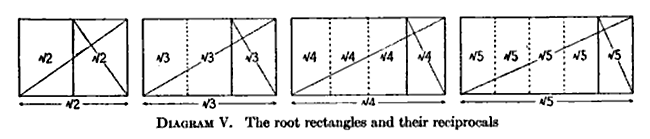
- Kiedy prostokąt o pierwiastku N jest dzielony na N przystających prostokątów przez podzielenie dłuższej krawędzi na N segmentów, otrzymane figury zachowują proporcję pierwiastka- N (jak pokazano powyżej).
- Prostokąt pierwiastkowy 3 jest również nazywany sześciokątem , a jego krótszy i dłuższy bok są proporcjonalnie równoważne z bokiem i średnicą sześciokąta .
- Ponieważ 2 jest pierwiastkiem kwadratowym z 4, prostokąt pierwiastkowy z 4 ma proporcje 1:2, co oznacza, że odpowiada dwóm kwadratom ułożonym obok siebie.
- Prostokąt pierwiastkowy 5 jest powiązany ze złotym podziałem (φ). Dłuższy bok jest równy jeden plus dwa razy 1/φ (0,618...).
Prostokąt pierwiastkowy φ

Prostokąt root-φ jest prostokątem dynamicznym, ale nie prostokątem głównym. Jego przekątna jest równa φ razy długości krótszego boku. Jeśli prostokąt o pierwiastku φ zostanie podzielony przez przekątną, otrzymamy dwa przystające trójkąty Keplera .
Jaya Hambidge'a
Jay Hambidge , jako część swojej teorii dynamicznej symetrii, zawiera pierwiastki prostokątne w tym, co nazywa dynamicznymi prostokątami , które mają niewymierne i geometryczne ułamki jako proporcje, takie jak złoty podział lub pierwiastki kwadratowe. Hambidge odróżnia je od prostokątów o wymiernych proporcjach, które nazywa prostokątami statycznymi . Według niego prostokąty o pierwiastkach 2, 3, 4 i 5 są często spotykane w gotyckiej i klasycznej greckiej i rzymskiej sztuce, przedmiotach i architekturze, podczas gdy prostokąty o proporcjach większych niż pierwiastek 5 są rzadko spotykane w projektach ludzkich.
Według Matila Ghyka , dynamiczne prostokąty Hambidge'a
może wytworzyć najbardziej zróżnicowane i zadowalające harmoniczne (spółgłoski, powiązane symetrią) podziały i kombinacje, a to przez bardzo prosty proces [...] rysowania wewnątrz wybranego prostokąta przekątnej i prostopadłej do niej z jednego z dwóch pozostałych wierzchołków (podział powierzchni na prostokąt odwrotny i jego gnomon) oraz rysowanie dowolnej sieci równoleżników i prostopadłych do boków i przekątnych. Tworzy to automatycznie powierzchnie skorelowane z charakterystyczną proporcją początkowego prostokąta, a także pozwala uniknąć (ponownie automatycznie) mieszania antagonistycznych motywów, takich jak √ 2 i √ 3 lub √ 5 . √ 5 i Φ przeciwnie, nie są antagonistyczne, ale zgodne, także z √ Φ , Φ 2 , itd.
12 ortogonów Wersina
Według Wolfganga von Wersina The Book of Rectangles, Spatial Law and Gestures of The Orthogons Described (1956), zestaw 12 specjalnych ortogonów (z gr. ορθος , orthos , „prosty” i γονια , gonia , „kąt” ; „figura pod kątem prostym”, która w konsekwencji jest prostokątna i czworokątna ) była historycznie używana przez artystów, architektów i kaligrafów do kierowania rozmieszczeniem i interakcją elementów w projekcie. Te ortogonony to:
- Kwadrat (1:1 lub 1: √ 1 )
- Przekątna (1: √ 2 )
- Hekton lub sześćton (1: √ 3 )
- Doppelquadrat (1:2 lub 1: √ 4 )
- Hemiolion (2:3)
- Auron ( złoty prostokąt , 1: φ )
- Hemidiagon (1:½ √ 5 )
- Pentona (1: √ φ )
- Trion (1:⅔ √ 3 )
- Czworokąt (1:(1+ √ 2 )/2)
- Biauron (1:2φ)
- Bipenton (1:2 √ 5-2 √ 5 )
Książka Wolfganga von Wersina zawiera niezwykłą kopię tekstu z roku 1558 ( Renesans ), z diagramami siedmiu z 12 ortogonów i zaproszeniem z tego fragmentu do zwrócenia bacznej uwagi, ponieważ „starożytni” architekci wierzyli, że „nic nie przewyższa tych proporcji”, jak „rzecz najczystszej abstrakcji”.
Wszystkie 12 ortogonów, gdy są uformowane razem, tworzą całą jednostkę: kwadrat, który rozwinął się w podwójny kwadrat.
Być może najbardziej popularnym wśród ortogonów jest auron lub złoty prostokąt , który jest tworzony przez rzutowanie przekątnej biegnącej od środkowego punktu boku kwadratu do jednego z przeciwległych wierzchołków, aż do wyrównania z punktem środkowym.
Cztery z tych ortogonów to harmoniczne prostokąty: przekątna lub pierwiastek 2 jest tworzony przez rzutowanie przekątnej kwadratu; sześciokąt , hekton lub pierwiastek 3 jest tworzony przez rzutowanie przekątnej przekątnej; podwójny kwadrat lub prostokąt pierwiastkowy 4 jest tworzony przez rzutowanie przekątnej hektonu; prostokąt pierwiastkowy 5 jest tworzony przez rzutowanie przekątnej podwójnego kwadratu (lub rzutowanie o 180 ° obu przekątnych, które biegną od środkowego punktu boku kwadratu do przeciwległych wierzchołków).
Dwie z najbardziej skomplikowanych z tych liczb to; penton , o proporcjach 1: √ φ odnosi się do przekroju złotej piramidy , dłuższy bok bipentonu jest równy krótszemu pomnożonemu przez dwie trzecie pierwiastka kwadratowego z trzech, dłuższy bok biauronu to √ 5 - 1 lub 2τ razy krótszy.
Czworokąt jest powiązany z przekątną w tym sensie, że jego dłuższy bok jest tworzony przez rzutowanie przekątnej ćwiartki kwadratu. Trion i szerokość boku. Hemidiagon (1:½ √ 5 ) dłuższy bok jest połową boku pierwiastka z 5 prostokąta i jest tworzony przez rzutowanie przekątnej połowy kwadratu, aż będzie prostopadła do początku układu współrzędnych .
Oprócz kwadratu i podwójnego kwadratu jedynym innym statycznym prostokątem zawartym na liście jest hemiolion , który jest tworzony przez rzutowanie połowy boku kwadratu pod kątem 90° lub 180°.
Konstruowanie ortogonu
Wymiary ortogonów odnoszą się do siebie nawzajem i do ortogonu jako całości. Z tego powodu wykorzystanie Orthogonów jako szablonu lub podkonstrukcji jest przedmiotem zainteresowania artystów, architektów i projektantów.
Ortogony zawsze zaczynają się od kwadratu, dowolnego kwadratu. Po zbudowaniu indywidualnego ortogonu określane są dodatkowe powiązane pomiary (mały, średni, duży). Pomiary te można następnie wykorzystać do prowadzenia projektu (malarstwo, architektura, ceramika, meble, kaligrafia, auto itp.).
Dostępne są diagramy dla wszystkich dwunastu ortogonów.
Książka Wersina zawiera bardzo szczegółowe wyjaśnienia dotyczące tworzenia poszczególnych ortogonów. Uzyskane pomiary są następnie stosowane w projekcie. Grafika Giorgio Morandiego jest przykładem tego, jak pomiary różnych rozmiarów (pochodzące z ortogonu) mogą tworzyć wizualną harmonię.
Ortogony i projektowanie
Użycie wymiarów związanych z ortogonem jako systemu podkonstrukcji (lub szablonu projektu) gwarantuje, że różne części będą odnosić się do projektu jako całości. Marcus Vitruvius Pollio w trzeciej księdze „ De Architectura ” (znanej obecnie jako „Dziesięć ksiąg architektury”) wyjaśnia:
„Dlatego, ponieważ natura tak zaprojektowała ludzkie ciało, aby jego człony były odpowiednio proporcjonalne do szkieletu jako całości, wydaje się, że starożytni mieli dobry powód, by rządzić, że w doskonałych budynkach różne człony muszą być w dokładnych symetrycznych stosunkach, aby cały ogólny schemat. Stąd, przekazując nam odpowiednie aranżacje dla wszelkiego rodzaju budynków, byli szczególnie ostrożni, aby to zrobić w przypadku świątyń bogów, budynków, w których zalety i wady zwykle trwają wiecznie.
Rysunek Leonarda przedstawiający Człowieka witruwiańskiego jest ilustracją koncepcji części odnoszących się do dzieła jako całości.
Dalsza lektura
- Hemenway, Priya; Boska proporcja, Phi w sztuce, przyrodzie i nauce; 2005, Sterling Publishing Co., Inc, NY, NY.