IEEE 754-1985

IEEE 754-1985 był branżowym standardem reprezentacji liczb zmiennoprzecinkowych w komputerach , oficjalnie przyjętym w 1985 roku i zastąpionym w 2008 roku przez IEEE 754-2008 , a następnie ponownie w 2019 roku przez niewielką poprawkę IEEE 754-2019 . Przez 23 lata był to najczęściej używany format obliczeń zmiennoprzecinkowych. bibliotek zmiennoprzecinkowych , oraz sprzętowo, w instrukcjach wielu CPU i FPU . Pierwszy układem scalonym do realizacji projektu tego, co miało stać się IEEE 754-1985, był Intel 8087 .

IEEE 754-1985 przedstawia liczby w systemie binarnym , dostarczając definicje dla czterech poziomów dokładności, z których dwa najczęściej używane to:

Poziom Szerokość Zasięg z pełną precyzją Precyzja
Pojedyncza precyzja 32 bity ±1,18 × 10 −38 do ±3,4 × 10 38 Około 7 cyfr dziesiętnych
Podwójna precyzja 64 bity ±2,23 × 10 −308 do ±1,80 × 10 308 Około 16 cyfr dziesiętnych

Norma definiuje również reprezentacje dodatniej i ujemnej nieskończoności , „ ujemne zero ”, pięć wyjątków do obsługi nieprawidłowych wyników, takich jak dzielenie przez zero , specjalne wartości zwane NaN do reprezentowania tych wyjątków, liczby denormalne do reprezentowania liczb mniejszych niż pokazano powyżej oraz cztery zaokrąglenia tryby.

Reprezentacja liczb

Liczba 0,15625 reprezentowana jako liczba zmiennoprzecinkowa pojedynczej precyzji IEEE 754-1985. Zobacz tekst w celu wyjaśnienia.
Trzy pola w 64-bitowym zmiennoprzecinkowym IEEE 754

Liczby zmiennoprzecinkowe w formacie IEEE 754 składają się z trzech pól: bitu znaku , obciążonego wykładnika i ułamka. Poniższy przykład ilustruje znaczenie każdego z nich.

Liczba dziesiętna 0,15625 10 reprezentowana w systemie binarnym to 0,00101 2 (czyli 1/8 + 1/32). (Indeksy dolne oznaczają podstawę liczby .) Analogicznie do notacji naukowej , gdzie liczby są zapisywane z pojedynczą cyfrą różną od zera po lewej stronie przecinka dziesiętnego, przepisujemy tę liczbę tak, aby miała pojedynczy 1 bit na lewo od „ punkt binarny". Po prostu mnożymy przez odpowiednią potęgę liczby 2, aby zrekompensować przesunięcie bitów w lewo o trzy pozycje:

Teraz możemy odczytać ułamek i wykładnik: ułamek to 0,01 2 , a wykładnik to −3.

Jak pokazano na rysunkach, trzy pola w reprezentacji IEEE 754 tej liczby to:

znak = 0, ponieważ liczba jest dodatnia. (1 oznacza ujemne).
Wykładnik obciążony = −3 + „odchylenie”. W pojedynczej precyzji odchylenie wynosi 127 , więc w tym przykładzie obciążony wykładnik wynosi 124; w przypadku podwójnej precyzji obciążenie wynosi 1023 , więc wykładnik obciążony w tym przykładzie wynosi 1020.
ułamek = 0,01000… 2 .

IEEE 754 dodaje odchylenie do wykładnika, dzięki czemu liczby można w wielu przypadkach wygodnie porównywać za pomocą tego samego sprzętu, który porównuje liczby całkowite z dopełnieniem do dwóch ze znakiem . Używając obciążonego wykładnika, mniejsza z dwóch dodatnich liczb zmiennoprzecinkowych wyjdzie „mniejsza niż” większa, zgodnie z tym samym uporządkowaniem, co w przypadku znaku i wielkości liczby całkowite. Jeśli dwie liczby zmiennoprzecinkowe mają różne znaki, porównanie znaku i wielkości działa również z obciążonymi wykładnikami. Jeśli jednak obie liczby zmiennoprzecinkowe o odchylonym wykładniku są ujemne, kolejność musi zostać odwrócona. Gdyby wykładnik był reprezentowany jako, powiedzmy, liczba dopełniona do 2, porównanie w celu sprawdzenia, która z dwóch liczb jest większa, nie byłoby tak wygodne.

Początkowy bit 1 jest pomijany, ponieważ wszystkie liczby z wyjątkiem zera zaczynają się od wiodącej cyfry 1; wiodąca 1 jest niejawna i tak naprawdę nie musi być przechowywana, co daje dodatkową odrobinę precyzji dla „darmowego”.

Zero

Liczba zero jest reprezentowana specjalnie:

znak = 0 dla dodatniego zera , 1 dla ujemnego zera .
obciążony wykładnik = 0.
ułamek = 0.

Liczby zdenormalizowane

Opisane powyżej reprezentacje liczb są nazywane znormalizowanymi, co oznacza, że ​​niejawną wiodącą cyfrą binarną jest 1. Aby zmniejszyć utratę precyzji w przypadku wystąpienia niedomiaru , IEEE 754 zawiera możliwość reprezentowania ułamków mniejszych niż jest to możliwe w znormalizowanej reprezentacji, poprzez niejawna cyfra wiodąca a 0. Takie liczby nazywane są denormalnymi . Nie zawierają tylu cyfr znaczących , co liczba znormalizowana, ale umożliwiają stopniową utratę precyzji, gdy wynik operacji nie jest dokładnie zerem, ale jest zbyt bliski zeru, aby można go było przedstawić za pomocą znormalizowanej liczby.

Liczba denormalna jest reprezentowana przez obciążony wykładnik wszystkich bitów 0, co reprezentuje wykładnik -126 w pojedynczej precyzji (nie -127) lub -1022 w podwójnej precyzji (nie -1023). Natomiast najmniejszy obciążony wykładnik reprezentujący liczbę normalną to 1 (patrz przykłady poniżej).

Reprezentacja liczb niebędących liczbami

Pole odchylonego wykładnika jest wypełnione wszystkimi bitami 1, aby wskazać nieskończoność lub nieprawidłowy wynik obliczeń.

Nieskończoność dodatnia i ujemna

Dodatnia i ujemna nieskończoność są reprezentowane w następujący sposób:

znak = 0 dla dodatniej nieskończoności, 1 dla ujemnej nieskończoności.
obciążony wykładnik = wszystkie 1 bity.
ułamek = wszystkie 0 bitów.

NaN

Niektóre operacje arytmetyki zmiennoprzecinkowej są nieprawidłowe, na przykład pierwiastek kwadratowy z liczby ujemnej. Osiągnięcie nieprawidłowego wyniku jest nazywane wyjątkiem zmiennoprzecinkowym. Wyjątkowy wynik jest reprezentowany przez specjalny kod o nazwie NaN, oznaczający „ Not a Number ”. Wszystkie NaN w IEEE 754-1985 mają ten format:

znak = albo 0 albo 1.
obciążony wykładnik = wszystkie 1 bity.
ułamek = wszystko oprócz wszystkich bitów 0 (ponieważ wszystkie bity 0 reprezentują nieskończoność).

Zasięg i precyzja

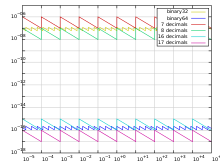
Względna precyzja liczb o pojedynczej (binary32) i podwójnej precyzji (binary64) w porównaniu z reprezentacjami dziesiętnymi przy użyciu stałej liczby cyfr znaczących . Precyzja względna jest tutaj zdefiniowana jako ulp( x )/ x , gdzie ulp ( x ) jest jednostką na ostatnim miejscu w reprezentacji x , czyli odstępem między x a następną reprezentowalną liczbą.

Precyzja jest definiowana jako minimalna różnica między dwoma kolejnymi reprezentacjami mantysy; jest to zatem funkcja tylko w mantysie; podczas gdy przerwa jest definiowana jako różnica między dwiema kolejnymi liczbami.

Pojedyncza precyzja

pojedynczej precyzji zajmują 32 bity. W pojedynczej precyzji:

  • Liczby dodatnie i ujemne najbliższe zeru (reprezentowane przez zdenormalizowaną wartość ze wszystkimi zerami w polu wykładnika i wartością binarną 1 w polu ułamka) to
    ±2 −23 × 2 −126 ≈ ± 1,40130 × 10 −45
  • Dodatnie i ujemne znormalizowane liczby najbliższe zeru (reprezentowane przez wartość binarną 1 w polu wykładnika i 0 w polu ułamka) to
    ± 1 × 2 −126 ≈ ± 1,17549 × 10 −38
  • Skończone liczby dodatnie i skończone ujemne najbardziej oddalone od zera (reprezentowane przez wartość z 254 w polu wykładnika i same jedynki w polu ułamka) to
    ±(2−2 −23 ) × 2 127 ≈ ±3,40282 × 10 38

Niektóre przykładowe wartości zakresu i przerwy dla danych wykładników w pojedynczej precyzji:

Rzeczywisty wykładnik (nieobciążony) Exp (stronniczy) Minimum Maksymalny Luka
−1 126 0,5 ≈ 0,999999940395 ≈ 5,96046e-8
0 127 1 ≈ 1,999999880791 ≈ 1.19209e-7
1 128 2 ≈ 3,999999761581 ≈ 2,38419e-7
2 129 4 ≈ 7,999999523163 ≈ 4,76837e-7
10 137 1024 ≈ 2047.999877930 ≈ 1,22070e-4
11 138 2048 ≈ 4095,999755859 ≈ 2,44141e-4
23 150 8388608 16777215 1
24 151 16777216 33554430 2
127 254 ≈ 1,70141e38 ≈ 3,40282e38 ≈ 2,02824e31

Na przykład 16 777 217 nie może być zakodowane jako 32-bitowa liczba zmiennoprzecinkowa, ponieważ zostanie zaokrąglona do 16 777 216. To pokazuje, dlaczego arytmetyka zmiennoprzecinkowa jest nieodpowiednia dla oprogramowania księgowego. Jednak wszystkie liczby całkowite w reprezentowalnym zakresie, które są potęgą 2, mogą być przechowywane w 32-bitowej liczbie zmiennoprzecinkowej bez zaokrąglania.

Podwójna precyzja

podwójnej precyzji zajmują 64 bity. W podwójnej precyzji:

  • Liczby dodatnie i ujemne najbliższe zeru (reprezentowane przez zdenormalizowaną wartość z samymi zerami w polu Exp i wartością binarną 1 w polu Ułamek) to
    ±2 −52 × 2 −1022 ≈ ±4,94066 × 10 −324
  • Dodatnie i ujemne znormalizowane liczby najbliższe zeru (reprezentowane przez wartość binarną 1 w polu Exp i 0 w polu ułamka) to
    ±1 × 2 −1022 ≈ ±2,22507 × 10 −308
  • Skończone dodatnie i skończone liczby ujemne najbardziej oddalone od zera (reprezentowane przez wartość z 2046 w polu Exp i same jedynki w polu ułamka) to
    ±(2−2 −52 ) × 2 1023 ≈ ± 1,79769 × 10 308

Niektóre przykładowe wartości zakresu i przerwy dla danych wykładników w podwójnej precyzji:

Rzeczywisty wykładnik (nieobciążony) Exp (stronniczy) Minimum Maksymalny Luka
−1 1022 0,5 ≈ 0,999999999999999888978 ≈ 1.11022e-16
0 1023 1 ≈ 1,999999999999999777955 ≈ 2,22045e-16
1 1024 2 ≈ 3,999999999999999555911 ≈ 4,44089e-16
2 1025 4 ≈ 7,999999999999999111822 ≈ 8,88178e-16
10 1033 1024 ≈ 2047.999999999999772626 ≈ 2,27374e-13
11 1034 2048 ≈ 4095,999999999999545253 ≈ 4,54747e-13
52 1075 4503599627370496 9007199254740991 1
53 1076 9007199254740992 18014398509481982 2
1023 2046 ≈ 8,98847e307 ≈ 1,79769e308 ≈ 1,99584e292

Rozszerzone formaty

Norma zaleca również stosowanie formatów rozszerzonych do wykonywania obliczeń wewnętrznych z większą precyzją niż wymagana dla wyniku końcowego, aby zminimalizować błędy zaokrągleń: norma określa jedynie wymagania dotyczące minimalnej precyzji i wykładników dla takich formatów. 80-bitowy rozszerzony format x87 jest najczęściej wdrażanym formatem rozszerzonym, który spełnia te wymagania .

Przykłady

Oto kilka przykładów reprezentacji pojedynczej precyzji IEEE 754:

Typ Podpisać Rzeczywisty wykładnik Exp (stronniczy) Pole wykładnika Pole ułamkowe Wartość
Zero 0 −126 0 0000 0000 000 0000 0000 0000 0000 0000 0,0
Ujemne zero 1 −126 0 0000 0000 000 0000 0000 0000 0000 0000 −0,0
Jeden 0 0 127 0111 1111 000 0000 0000 0000 0000 0000 1.0
Minus jeden 1 0 127 0111 1111 000 0000 0000 0000 0000 0000 −1,0
Najmniejsza liczba zdenormalizowana * −126 0 0000 0000 000 0000 0000 0000 0000 0001 ±2 −23 × 2 −126 = ±2 −149 ≈ ±1,4 × 10 −45
„Środkowa” liczba zdenormalizowana * −126 0 0000 0000 100 0000 0000 0000 0000 0000 ±2 −1 × 2 −126 = ±2 −127 ≈ ±5,88 × 10 −39
Największa liczba zdenormalizowana * −126 0 0000 0000 111 1111 1111 1111 1111 1111 ±(1−2 −23 ) × 2 −126 ≈ ±1,18 × 10 −38
Najmniejsza liczba znormalizowana * −126 1 0000 0001 000 0000 0000 0000 0000 0000 ±2 −126 ≈ ±1,18 × 10 −38
Największa znormalizowana liczba * 127 254 1111 1110 111 1111 1111 1111 1111 1111 ±(2−2 −23 ) × 2 127 ≈ ±3,4 × 10 38
Pozytywna nieskończoność 0 128 255 1111 1111 000 0000 0000 0000 0000 0000 +∞
Ujemna nieskończoność 1 128 255 1111 1111 000 0000 0000 0000 0000 0000 −∞
Nie liczba * 128 255 1111 1111 niezerowe NaN
* Bit znaku może mieć wartość 0 lub 1 .

Porównywanie liczb zmiennoprzecinkowych

Każda możliwa kombinacja bitów jest albo NaN, albo liczbą o unikalnej wartości w afinicznie rozszerzonym systemie liczb rzeczywistych wraz z powiązanym porządkiem, z wyjątkiem dwóch kombinacji bitów dla ujemnego zera i dodatniego zera, które czasami wymagają szczególnej uwagi (patrz poniżej) . Reprezentacja binarna ma tę specjalną właściwość, że z wyłączeniem NaN dowolne dwie liczby można porównać jako liczby całkowite znaku i wielkości ( obowiązują problemy z endianizmem ). Porównując jako uzupełnienie do 2 liczby całkowite: Jeśli bity znaku są różne, liczba ujemna poprzedza liczbę dodatnią, więc uzupełnienie do 2 daje prawidłowy wynik (z wyjątkiem tego, że ujemne zero i dodatnie zero należy uznać za równe). Jeśli obie wartości są dodatnie, porównanie uzupełnienia do 2 ponownie daje poprawny wynik. W przeciwnym razie (dwie liczby ujemne) prawidłowe uporządkowanie FP jest przeciwieństwem uporządkowania uzupełnienia do 2.

Błędy zaokrągleń nieodłącznie związane z obliczeniami zmiennoprzecinkowymi mogą ograniczać użycie porównań do sprawdzania dokładnej równości wyników. Wybór akceptowalnego zakresu to złożony temat. Powszechną techniką jest użycie wartości porównania epsilon do przeprowadzenia przybliżonych porównań. W zależności od tego, jak łagodne są porównania, wspólne wartości obejmują 1e-6 lub 1e-5 dla pojedynczej precyzji i 1e-14 dla podwójnej precyzji. Inną powszechną techniką jest ULP, która sprawdza, jaka jest różnica w cyfrach ostatniego miejsca, skutecznie sprawdzając, o ile kroków dzielą te dwie wartości.

Chociaż ujemne zero i dodatnie zero są ogólnie uważane za równe dla celów porównawczych, niektóre operatory relacyjne języka programowania i podobne konstrukcje traktują je jako różne. Zgodnie ze Java , operatory porównania i równości traktują je jako równe, ale rozróżniają je Math.min() i Math.max() (oficjalnie począwszy od Javy w wersji 1.1, ale w rzeczywistości od 1.1.1), podobnie jak metody porównawcze equals() , CompareTo() a nawet Compare() klas Float i podwójny .

Zaokrąglanie liczb zmiennoprzecinkowych

Standard IEEE ma cztery różne tryby zaokrąglania; pierwsza jest domyślna; inne nazywane są zaokrągleniami skierowanymi .

  • Round to Nearest – zaokrągla do najbliższej wartości; jeśli liczba wypada w połowie, jest zaokrąglana do najbliższej wartości z parzystym (zerem) najmniej znaczącym bitem, co oznacza, że ​​jest zaokrąglana w górę w 50% przypadków (w IEEE 754-2008 ten tryb nazywa się roundTiesToEven , aby odróżnić go od innej rundy -do najbliższego trybu)
  • Zaokrąglenie do 0 – zaokrąglenie skierowane do zera
  • Zaokrąglenie w kierunku +∞ – zaokrąglenie skierowane w kierunku dodatniej nieskończoności
  • Zaokrąglenie w kierunku −∞ – zaokrąglenie skierowane w kierunku ujemnej nieskończoności.

Rozszerzanie liczb rzeczywistych

Standard IEEE wykorzystuje (i rozszerza) afinicznie rozszerzony system liczb rzeczywistych , z oddzielnymi dodatnimi i ujemnymi nieskończonościami. Podczas opracowywania pojawiła się propozycja, aby standard obejmował rozszerzony projektowo system liczb rzeczywistych z pojedynczą nieskończonością bez znaku, poprzez zapewnienie programistom opcji wyboru trybu. Jednak w celu zmniejszenia złożoności ostatecznego standardu zrezygnowano z trybu projekcyjnego. Koprocesory zmiennoprzecinkowe Intel 8087 i Intel 80287 obsługują ten tryb projekcyjny .

Funkcje i predykaty

Operacje standardowe

Należy zapewnić następujące funkcje:

Zalecane funkcje i predykaty

  • copysign(x,y) zwraca x ze znakiem y, więc abs(x) równa się copysign(x,1.0) . Jest to jedna z niewielu operacji, które działają na NaN w sposób przypominający arytmetykę. Funkcja copysign jest nowością w standardzie C99.
  • −x zwraca x z odwróconym znakiem. W niektórych przypadkach różni się to od 0-x, zwłaszcza gdy x wynosi 0. Zatem −(0) wynosi −0, ale znak 0−0 zależy od trybu zaokrąglania.
  • skala(y, N)
  • logb(x)
  • finite(x) predykat dla „ x jest wartością skończoną”, odpowiednik −Inf < x < Inf
  • isnan(x) predykat dla „x to NaN”, odpowiednik „x ≠ x”
  • x <> y , co okazuje się mieć inne zachowanie niż NOT(x = y) z powodu NaN.
  • unordered(x, y) jest prawdziwe, gdy „x jest nieuporządkowane z y”, tj. x lub y jest NaN.
  • klasa(x)
  • nextafter(x,y) zwraca następną reprezentowalną wartość od x w kierunku y

Historia

W 1976 roku Intel rozpoczął prace nad koprocesorem zmiennoprzecinkowym . Intel miał nadzieję, że będzie w stanie sprzedać układ zawierający dobre implementacje wszystkich operacji występujących w bardzo różnych bibliotekach oprogramowania matematycznego.

John Palmer, który kierował projektem, uważał, że wysiłki powinny być wspierane przez standardowe ujednolicenie operacji zmiennoprzecinkowych na różnych procesorach. Skontaktował się z Williamem Kahanem z Uniwersytetu Kalifornijskiego , który pomógł poprawić dokładność kalkulatorów firmy Hewlett-Packard . Kahan zasugerował, aby Intel użył liczby zmiennoprzecinkowej VAX firmy Digital Equipment Corporation (DEC). Pierwszy VAX, VAX-11/780 pojawił się dopiero pod koniec 1977 roku, a jego zmiennoprzecinkowy był wysoko ceniony. Jednak starając się wprowadzić swój chip na jak najszerszy rynek, Intel chciał możliwie najlepszego zmiennoprzecinkowego, a Kahan przystąpił do sporządzenia specyfikacji. Kahan początkowo zalecał, aby podstawa zmiennoprzecinkowa była dziesiętna [ niewiarygodne źródło? ] , ale projekt sprzętu koprocesora był zbyt zaawansowany, aby wprowadzić tę zmianę.

Praca w firmie Intel zaniepokoiła innych dostawców, którzy podjęli działania standaryzacyjne, aby zapewnić „równe szanse”. Kahan wziął udział w drugim spotkaniu grupy roboczej ds. standardów IEEE 754, które odbyło się w listopadzie 1977 r. Następnie otrzymał pozwolenie od firmy Intel na przedstawienie projektu propozycji opartej na jego pracy dla ich koprocesora; pozwolono mu wyjaśnić szczegóły formatu i jego uzasadnienie, ale nie cokolwiek związanego z architekturą implementacji Intela. Szkic został napisany wspólnie z Jerome'em Coonenem i Haroldem Stone'em i początkowo był znany jako „propozycja Kahan-Coonen-Stone” lub „format KCS”.

Ponieważ 8-bitowy wykładnik nie był wystarczająco szeroki dla niektórych operacji pożądanych dla liczb podwójnej precyzji, np. Do przechowywania iloczynu dwóch liczb 32-bitowych, zarówno propozycja Kahana, jak i kontrpropozycja DEC wykorzystywały 11 bitów, podobnie jak czas -przetestowany 60-bitowy format zmiennoprzecinkowy CDC 6600 z 1965 roku. Propozycja Kahana przewidywała również nieskończoności, przydatne przy dzieleniu przez zero; wartości nieliczbowe, które są przydatne w przypadku niepoprawnych operacji; liczby denormalne , które pomagają złagodzić problemy spowodowane niedomiarem; i lepiej zrównoważone odchylenie wykładnicze , co może pomóc uniknąć przepełnienia i niedomiaru podczas obliczania odwrotności liczby.

Jeszcze przed zatwierdzeniem projekt normy został wdrożony przez wielu producentów. Intel 8087, który został ogłoszony w 1980 roku, był pierwszym chipem, który zaimplementował projekt standardu.

Koprocesor zmiennoprzecinkowy Intel 8087

W 1980 roku chip Intel 8087 został już wypuszczony, ale DEC pozostał przeciwny, w szczególności liczbom odbiegającym od normalnych, ze względu na obawy dotyczące wydajności i ponieważ dałoby to DEC przewagę konkurencyjną w standaryzacji formatu DEC.

Spór o stopniowy niedostatek trwał do 1981 r., kiedy to ekspert zatrudniony przez DEC do jego oceny stanął po stronie dysydentów. DEC zlecił wykonanie badania, aby wykazać, że stopniowy niedopływ był złym pomysłem, ale badanie wykazało coś przeciwnego i DEC się poddał. W 1985 r. standard został ratyfikowany, ale de facto stał się już standardem rok wcześniej, wdrażane przez wielu producentów.

Zobacz też

Notatki

Dalsza lektura

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=IEEE_754-1985&oldid=1124829664 ”