Natychmiastowy środek obrotu

Szkic 1: Chwilowy środek P poruszającej się płaszczyzny

środek obrotu (również chwilowy środek prędkości , chwilowy środek lub chwilowy środek ) to punkt zamocowany na ciele poruszającym się po płaszczyźnie, które ma zerową prędkość w określonej chwili. W tej chwili wektory prędkości innych punktów ciała generują wokół tego punktu pole kołowe, które jest identyczne z polem generowanym przez czysty obrót.

Płaski ruch ciała jest często opisywany za pomocą płaskiej figury poruszającej się po dwuwymiarowej płaszczyźnie . Chwilowe centrum to punkt na ruchomej płaszczyźnie, wokół którego obracają się wszystkie inne punkty w określonej chwili.

Ciągły ruch płaszczyzny ma natychmiastowe centrum dla każdej wartości parametru czasu. Generuje to krzywą zwaną ruchomym środkiem ciężkości . Punkty na ustalonej płaszczyźnie odpowiadające tym chwilowym środkom tworzą stałą centrodę.

Uogólnienie tej koncepcji na przestrzeń trójwymiarową polega na skręcie wokół śruby. Śruba ma oś, która jest linią w przestrzeni 3D (niekoniecznie przez początek), a śruba ma również skończony skok (stałe przesunięcie wzdłuż jej osi odpowiadające obrotowi wokół osi śruby).

Biegun płaskiego przemieszczenia

Szkic 2: Biegun płaskiego przemieszczenia

Chwilowe centrum można uznać za graniczny przypadek bieguna płaskiego przemieszczenia.

Planarne przemieszczenie ciała z pozycji 1 do pozycji 2 jest definiowane przez kombinację płaskiego obrotu i płaskiego translacji . Dla każdego płaskiego przemieszczenia istnieje punkt w poruszającym się ciele, który znajduje się w tym samym miejscu przed i po przemieszczeniu. Ten punkt jest biegunem przemieszczenia planarnego , a przemieszczenie można postrzegać jako obrót wokół tego bieguna.

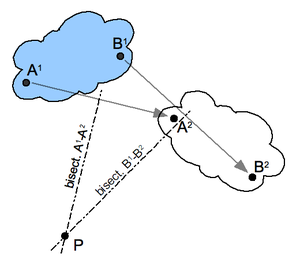
Konstrukcja bieguna przemieszczenia planarnego: Najpierw wybierz dwa punkty A i B w poruszającym się ciele i zlokalizuj odpowiadające im punkty w obu pozycjach; patrz ilustracja. Skonstruuj dwusieczne prostopadłe do dwóch odcinków A ¹ A ² i B ¹ B ² . Przecięcie P tych dwóch dwusiecznych jest biegunem przemieszczenia planarnego. Zauważ, że A ¹ i A ² leżą na okręgu wokół P. Dotyczy to odpowiednich pozycji każdego punktu w ciele.

Jeśli dwa położenia ciała są oddzielone momentem czasu w ruchu planarnym, to biegun przemieszczenia staje się natychmiastowym środkiem. W tym przypadku odcinki utworzone między chwilowymi położeniami punktów A i B stają się wektorami prędkości V _A i V _B . Linie prostopadłe do tych wektorów prędkości przecinają się w centrum chwili.

Algebraiczną konstrukcję współrzędnych kartezjańskich $ZA$ następujący sposób: Punkt środkowy między $}}$ $^$ $współrzędne$ ma kartezjańskie

{\ Displaystyle A_ {x} ^ {m} = {\ Frac {1} {2}} \ lewo (A_ {x} ^ {1} + A_{x}^{2}\right);\quad A_{y}^{m}={\frac {1}{2}}\left(A_{y}^{1}+A_{y}^ {2}\prawo),}

a punkt środkowy między ${\ Displaystyle B ^ {1}}$ a ${\ Displaystyle B ^ {2}}$ ma współrzędne kartezjańskie

{\ Displaystyle B_ {x} ^ {m} = {\ Frac {1} {2}} \ lewo (B_ {x} ^ {1} + B_ {x} ^ {2} \ prawo); \ quad B_ { y}^{m}={\frac {1}{2}}\left(B_{y}^{1}+B_{y}^{2}\right).}

Dwa kąty od do i od do B 1 $Displaystyle B ^ {1}$ $do$ $B$ 2 $^ {2}$ mierzone przeciwnie do ruchu wskazówek zegara względem poziomu są określane przez

{\ Displaystyle \ tan \ tau _ {A }={\frac {A_{y}^{2}-A_{y}^{1}}{A_{x}^{2}-A_{x}^{1}}},\quad \tan \ tau _{B}={\frac {B_{y}^{2}-B_{y}^{1}}{B_{x}^{2}-B_{x}^{1}}},}

biorąc odpowiednie gałęzie stycznej . Niech środek obrotu ma odległości ${\ Displaystyle \ lewo (P_ {x}, P_ {y} \ prawej)} i$ ${\ Displaystyle d_ {A}}$ i ${\ displaystyle d_{B}}$ do dwóch punktów środkowych. Zakładając obrót zgodnie z ruchem wskazówek zegara (w przeciwnym razie zmień znak ): ${\ Displaystyle \ pi / 2}$

{\ Displaystyle {\ rozpocząć {wyrównane} P_ {x} & = A_ {x} ^ {m} + d_ {A} \ cos \ lewo (\ tau _ {A} - {\ Frac {\ pi} {2} }\right)\\&=B_{x}^{m}+d_{B}\cos \left(\tau _{B}-{\frac {\pi }{2}}\right);\\ P_{y}&=A_{y}^{m}+d_{A}\sin \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_ {y}^{m}+d_{B}\sin \left(\tau _{B}-{\frac {\pi}{2}}\right).\end{aligned}}}

Przepisz to jako niejednorodny układ równań liniowych 4 × 4 z 4 niewiadomymi (dwie odległości $):$ dwie współrzędne środka ${\ displaystyle P}$

{\ Displaystyle {\ rozpocząć {pmatrix} 1&0&-\ sin \tau _ {A}&0\\1&0&0&-\sin \tau _{B}\\0&1&\cos \tau _{A}&0\\0&1&0&\cos \ tau _{B}\end{pmatrix}}{\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\begin{ pmatrix}A_{x}^{m}\\B_{x}^{m}\\A_{y}^{m}\\B_{y}^{m}\end{pmatrix}}.}

Współrzędne środka obrotu to dwie pierwsze składowe wektora rozwiązania

{\ Displaystyle {\ rozpocząć {pmatrix} P_ {x} \\ P_ {y} \\ d_ {A} \\ d_ {B} \ koniec {pmatrix}} = {\ Frac {1} {\ sin \ lewo ( \tau _{A}-\tau _{B}\right)}}{\begin{pmatrix}\left(B_{y}^{m}-A_{y}^{m}\right)\sin \ tau _{A}\sin \tau _{B}+B_{x}^{m}\sin \tau _{A}\cos \tau _{B}-A_{x}^{m}\cos \ tau _{A}\sin \tau _{B}\\\left(A_{x}^{m}-B_{x}^{m}\right)\cos \tau _{A}\cos \tau _{B}+A_{y}^{m}\sin \tau _{A}\cos \tau _{B}-B_{y}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{B}+\left(B_{y}^{m}- A_{y}^{m}\right)\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{ A}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\\\end{pmacierz}}.}

Czyste tłumaczenie

Jeśli przemieszczenie między dwoma położeniami jest czystym przesunięciem, to dwusieczne prostopadłe odcinków A ¹ B ¹ i A ² B ² tworzą linie równoległe. Uważa się, że linie te przecinają się w punkcie na linii w nieskończoności , dlatego mówi się, że biegun tego płaskiego przemieszczenia „leży w nieskończoności” w kierunku prostopadłych dwusiecznych.

Na granicy czysta translacja staje się ruchem planarnym z równoległymi wektorami prędkości punktowej. W tym przypadku mówi się, że środek chwili leży w nieskończoności w kierunku prostopadłym do wektorów prędkości.

Natychmiastowe wyśrodkowanie koła toczącego się bez poślizgu

Szkic 3: Toczące się koło.

Chwilowy środek obrotu toczącego się koła z podziałem na punkty. Dzieląc toczące się koło na kilka punktów, można łatwiej zobaczyć, jak wszystkie punkty koła obracają się wokół jednego punktu w każdej chwili. Ten punkt jest natychmiastowym środkiem obrotu, pokazanym na czarno.

Rozważmy płaski ruch kołowego koła toczącego się bez poślizgu po liniowej drodze; patrz szkic 3. Koło obraca się wokół własnej osi M, co przekłada się w kierunku równoległym do drogi. Punkt styku koła P z drogą nie ślizga się, co oznacza, że punkt P ma zerową prędkość względem drogi. Tak więc w chwili, gdy punkt P na kole styka się z drogą, natychmiast staje się środkiem.

Zbiór punktów poruszającego się koła, które stają się natychmiastowymi środkami, to sam okrąg, który definiuje poruszające się centrum. Punkty na ustalonej płaszczyźnie, które odpowiadają tym chwilowym środkom, to linia drogi, która definiuje stałe centrum.

Wektor prędkości punktu A w kole jest prostopadły do odcinka AP i jest proporcjonalny do długości tego odcinka. W szczególności prędkości punktów w kole są określone przez prędkość kątową koła obracającego się wokół P. Wektory prędkości wielu punktów są zilustrowane na szkicu 3.

Im dalej punkt koła znajduje się od środka chwili P, tym proporcjonalnie większa jest jego prędkość. Dlatego punkt na górze koła porusza się w tym samym kierunku, co środek M koła, ale dwa razy szybciej, ponieważ jest dwa razy dalej od punktu P. Wszystkie punkty, które znajdują się w odległości równej promieniowi koła koło „r” z punktu P porusza się z tą samą prędkością co punkt M, ale w różnych kierunkach. Jest to pokazane dla punktu na kole, który ma taką samą prędkość jak M, ale porusza się w kierunku stycznym do okręgu wokół P.

Względny środek obrotu dla dwóch stykających się ciał płaskich

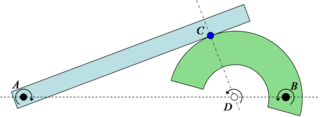
Szkic 4: Przykład względnego środka obrotu. Dwa ciała stykające się w punkcie C , jedno obracające się wokół A , a drugie wokół B , muszą mieć względny środek obrotu gdzieś wzdłuż linii AB . Ponieważ części nie mogą się przenikać, względny środek obrotu musi również znajdować się wzdłuż normalnego kierunku do styku i przez C . Jedynym możliwym rozwiązaniem jest sytuacja, w której środek względny znajduje się w D .

Jeśli dwa płaskie ciała sztywne stykają się, a każde ciało ma swój odrębny środek obrotu, to względny środek obrotu między ciałami musi leżeć gdzieś na linii łączącej te dwa środki. W rezultacie, ponieważ czyste toczenie może istnieć tylko wtedy, gdy środek obrotu znajduje się w punkcie styku (jak pokazano powyżej z kołem na drodze), to tylko wtedy, gdy punkt styku przechodzi przez linię łączącą dwa środki obrotu że można osiągnąć czyste toczenie. Jest to znane w przekładni ewolwentowej projekt jako punkt skoku, w którym nie ma względnego poślizgu między biegami. W rzeczywistości przełożenie między dwiema obracającymi się częściami określa się na podstawie stosunku dwóch odległości do względnego środka. W przykładzie na Szkicu 4 przełożenie wynosi ${\ Displaystyle \ gamma = {\ Frac {AD} {BD}}}$

Natychmiastowy środek obrotu i mechanizmy

Szkic 1 powyżej przedstawia połączenie z czterema prętami , na którym zilustrowano pewną liczbę natychmiastowych środków obrotu. Sztywny korpus oznaczony literami BAC jest połączony ogniwami P1 _- A i P2 _- B z podstawą lub ramą.

Trzy ruchome części tego mechanizmu (podstawa się nie porusza) to: ogniwo P ₁ -A, ogniwo P ₂ -B oraz korpus BAC. Dla każdej z tych trzech części można określić chwilowy środek obrotu.

Biorąc pod uwagę pierwsze połączenie P ₁ -A: wszystkie punkty na tym połączeniu, w tym punkt A, obracają się wokół punktu P ₁ . Ponieważ P ₁ jest jedynym punktem, który nie porusza się w danej płaszczyźnie, można go nazwać chwilowym środkiem obrotu tego połączenia. Punkt A, w odległości P ₁ -A od P ₁ , porusza się ruchem kołowym w kierunku prostopadłym do ogniwa P ₁ -A, jak wskazuje wektor V _A .

To samo dotyczy połączenia P ₂ -B: punkt P ₂ jest chwilowym środkiem obrotu tego połączenia, a punkt B porusza się w kierunku wskazanym przez wektor V _B .

Do wyznaczenia chwilowego środka obrotu trzeciego elementu łącznika, korpusu BAC, wykorzystuje się dwa punkty A i B, ponieważ znane są jego charakterystyki ruchowe, wynikające z informacji o ogniwach P 1 -A _i P ₂ - B.

Kierunek prędkości punktu A jest oznaczony wektorem V _A . Jego chwilowy środek obrotu musi być prostopadły do tego wektora (ponieważ V _A jest stycznie położony na obwodzie koła). Jedyną linią spełniającą to wymaganie jest linia współliniowa z łączem P ₁ -A. Gdzieś na tej prostej znajduje się punkt P, chwilowy środek obrotu ciała BAC.

To, co dotyczy punktu A, dotyczy również punktu B, dlatego ten chwilowy środek obrotu P leży na prostej prostopadłej do wektora VB _, prostej współliniowej z ogniwem P2 _- B. Dlatego chwilowy środek obrotu P ciała BAC jest punktem, w którym przecinają się linie przechodzące przez P1 _- A i P2 _- B.

Ponieważ ten chwilowy środek obrotu P jest środkiem wszystkich punktów na ciele BAC dla dowolnego przypadkowego punktu, powiedzmy punktu C, można wyznaczyć prędkość i kierunek ruchu: połącz P z C. Kierunek ruchu punktu C jest prostopadły do tego połączenia. Prędkość jest proporcjonalna do odległości do punktu P.

Kontynuując to podejście z dwoma ogniwami P1 _- A i P2 _- B obracającymi się wokół ich własnych chwilowych środków obrotu, można określić środek ciężkości dla chwilowego środka obrotu P. Na tej podstawie można określić ścieżkę ruchu dla C lub dowolnego innego punktu na ciele BAC.

Przykłady zastosowania

W badaniach biomechanicznych obserwuje się natychmiastowy środek rotacji dla funkcjonowania stawów kończyn górnych i dolnych. Na przykład podczas analizy kolanowych , skokowych lub barkowych . Taka wiedza pomaga w opracowywaniu sztucznych stawów i protez , takich jak stawy łokciowe czy palcowe.

Badanie stawów koni: „… wektory prędkości określone na podstawie chwilowych środków obrotu wskazywały, że powierzchnie stawów ślizgają się po sobie”.

Badania nad obracaniem statku poruszającego się po wodzie.

Charakterystykę hamowania samochodu można poprawić, zmieniając konstrukcję mechanizmu pedału hamulca.

Projektowanie zawieszenia roweru lub samochodu.

W przypadku ogniwa sprzęgającego w układzie czteroprętowym , takim jak zawieszenie z podwójnymi wahaczami poprzecznymi w widoku z przodu, prostopadłe do prędkości leżą wzdłuż ogniw łączących ogniwo uziemione z ogniwem sprzęgającym. Ta konstrukcja służy do ustalenia kinematycznego środka obrotu zawieszenia.

Zobacz też