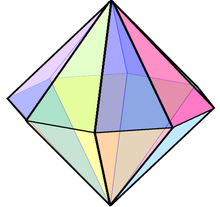
Ośmioboczna bipiramida

Ośmioboczna bipiramida
Ośmioboczna bipiramida
Typ	bipiramida
Twarze	16 trójkątów
Krawędzie	24
Wierzchołki	10
Symbol Schläfliego	{ } + {8}
Diagram Coxetera	;
Grupa symetrii	D 8h , [8,2], (*228), rząd 32
Grupa rotacyjna	D 8 , [8,2] + , (228), rząd 16
Podwójny wielościan	ośmiokątny pryzmat
Konfiguracja twarzy	V4.4.8
Nieruchomości	wypukła , twarz-przechodnia

Ośmiokątna bipiramida jest jednym z nieskończonego zestawu bipiramid , podwójnych do nieskończonych graniastosłupów . Jeśli ośmioboczna bipiramida ma być ścianą przechodnią , wszystkie ściany muszą być trójkątami równoramiennymi . 16-ścienne kości to często ośmioboczne bipiramidy.

Obrazy

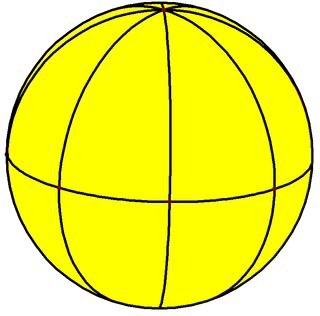
Można go narysować jako kafelek na kuli, która również reprezentuje podstawowe domeny symetrii [4,2], *422:

Powiązane wielościany

„Zwykłe” prawostronne (symetryczne) bipiramidy *n -gonalne:*
Nazwa bipiramidy	Digonalna bipiramida	Trójkątna bipiramida (patrz: J ₁₂ )	Kwadratowa bipiramida (patrz: O )	Pięciokątna bipiramida (patrz: J ₁₃ )	Sześciokątna bipiramida	Bipiramida siedmiokątna	Ośmioboczna bipiramida	Bipiramida enneagonalna	Dziesięciokątna bipiramida	...	Dwupiramida apeirogonalna
Obraz wielościanu										...
obraz kafelkowy										Obraz kafelkowy samolotu
Konfiguracja twarzy.	Wersja 2.4.4	Wersja 3.4.4	V4.4.4	V5.4.4	Wersja 6.4.4	Wersja 7.4.4	Wersja 8.4.4	Wersja 9.4.4	V10.4.4	...	V∞.4.4
Diagram Coxetera										...

* n 42 mutacja symetrii omnitruncated tilings: 4.8.2n
Symetria * n 42 [n,4]	Kulisty		euklidesowy	Kompaktowy hiperboliczny				parakomp.
Symetria * n 42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Omnitruced postać	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Podwójne omnitruncated	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞