Ścięte płytki tetraheksagonalne

Ścięty tetraheksagonalny kafelkowy
model dysku Poincarégo płaszczyzny hiperbolicznej
Typ	Hiperboliczne jednolite kafelkowanie
Konfiguracja wierzchołków	4.8.12
Symbol Schläfliego	tr {6,4} lub ${\ Displaystyle t {\ rozpocząć {Bmatrix} 6 \\ 4 \ koniec {Bmatrix}}}$
Symbol Wythoffa	2 6 4 |
Diagram Coxetera	Lub
Grupa symetrii	[6,4], (*642)
Podwójny	Zamów 4-6 płytek kisrhombille
Nieruchomości	Przechodnie wierzchołków

W geometrii ścięte czworokątne kafelki są półregularnymi kafelkami płaszczyzny hiperbolicznej. W każdym wierzchołku jest jeden kwadrat , jeden ośmiokąt i jeden dwunastokąt . Ma symbol Schläfliego tr{6,4}.

Podwójne układanie płytek

Podwójne kafelkowanie nazywane jest kafelkami kisrhombille rzędu 4-6 , wykonanymi jako kompletne przepołowienie sześciokątnego kafelka rzędu 4 , tutaj z trójkątami pokazanymi naprzemiennie kolorami. To kafelkowanie reprezentuje podstawowe trójkątne domeny symetrii [6,4] (*642).

Powiązane wielościany i tilings

* mutacja symetrii n 42 wielościennych pochyleń: 4.8.2n
Symetria * n 42 [n,4]	Kulisty		euklidesowy	Kompaktowy hiperboliczny				parakomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Omnitruced postać	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Podwójne omnitruncated	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

* nn 2 mutacje symetrii omnitruncated tilings: 4,2 n .2 n
Symetria * nn 2 [n,n]	Kulisty		euklidesowy	Kompaktowy hiperboliczny				parakomp.
	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Postać
Konfig.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Podwójny
Konfig.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	Wersja 4.12.12	V4.14.14	Wersja 4.16.16	V4.∞.∞

Z konstrukcji Wythoffa jest czternaście hiperbolicznych jednolitych nachyleń , które mogą być oparte na regularnym porządku - 4 sześciokątne kafelki.

Rysując kafelki w kolorze czerwonym na oryginalnych ścianach, żółtym w oryginalnych wierzchołkach i niebieskim wzdłuż oryginalnych krawędzi, jest 7 form z pełną [6,4] symetrią i 7 z subsymetrią.

Jednolite czworokątne nachylenie
Symetria : [6,4], (*642 ) (z [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (* 3222) indeks 2 podsymetrie) (I [(∞,3,∞,3)] (*3232) indeks 4 podsymetria)
= = =	=	= = =	=	= = =	=
{6,4}	t{6,4}	r{6,4}	t{4,6}	{4,6}	rrr{6,4}	tr{6,4}
Jednolite dublety
V6 4	Wersja 4.12.12	V(4.6) 2	Wersja 6.8.8	V4 6	V4.4.4.6	V4.8.12
Alternatywy
[1 + ,6,4] (*443)	[6 + ,4] (6*2)	[6,1 + ,4] (*3222)	[6,4 + ] (4*3)	[6,4,1 + ] (*662)	[(6,4,2 + )] (2*32)	[6,4] + (642)
=	=	=	=	=	=
h{6,4}	s{6,4}	godz.{6,4}	s{4,6}	h{4,6}	hrr{6,4}	sr{6,4}

Symetria

Ścięte czworokątne kafelki z lustrzanymi liniami w kolorze zielonym, czerwonym i niebieskim:

Diagramy symetrii dla podgrup o małym indeksie [6,4], pokazane w sześciokątnej komórce translacyjnej w kafelkach {6,6} , z podstawową domeną zaznaczoną na żółto.

Podwójność kafelkowania reprezentuje podstawowe domeny (*642) symetrii orbifoldu . Z [6,4] symetrii istnieje 15 małych podgrup indeksowych według operatorów usuwania lustra i przemienności . Lustra można usunąć, jeśli wszystkie jego rozkazy gałęzi są równe, i przecina sąsiednie zamówienia gałęzi o połowę. Usunięcie dwóch lusterek pozostawia punkt wirowania połowy rzędu, w którym spotkały się usunięte lustra. Na tych obrazach unikalne lustra są w kolorze czerwonym, zielonym i niebieskim, a naprzemiennie kolorowe trójkąty pokazują położenie punktów wirowania. [6 ⁺ ,4 ⁺ ], (32×) podgrupa ma wąskie linie reprezentujące odbicia poślizgu. Grupa indeksu podgrupy -8 , [1 ⁺ ,6,1 ⁺ ,4,1 ⁺ ] (3232) jest podgrupą komutatora [6,4].

Większa podgrupa skonstruowana jako [6,4*], usuwając punkty bezwładności [6,4 ⁺ ], (3*22), indeks 6 staje się ( *3333 ) i [6*,4], usuwając punkty bezwładności z [6 ⁺ ,4], (2*33), indeks 12 jako ( *222222 ). Wreszcie ich bezpośrednie podgrupy [6,4*] ⁺ , [6*,4] ⁺ , indeksy podgrup odpowiednio 12 i 24, można podać w notacji orbifold jako (3333) i (222222).

Małe podgrupy indeksowe [6,4]
Indeks	1	2			4
Diagram
Coxeter	[6,4] = =	[1 + ,6,4] =	[6,4,1 + ] = =	[6,1 + ,4] =	[1 + ,6,4,1 + ] =	[6 + ,4 + ]
Generatory	0 { , 1 , 2 }	{ 1 010 , 2 } _	0 { , 1 , 212 }	0 { , 101 , 2 , 121 }	{ 1 010 212 20102 } _ _ _	{012021}
Orbifold	*642	*443	*662	*3222	*3232	32×
Diagram
półprostych podgrup
Coxeter		[6,4 + ]	[6 + ,4]	[(6,4,2 + )]	[6,1 + ,4,1 + ] = = = =	[1 + ,6,1 + ,4] = = = =
Generatory		0 { ,12}	{01, 2 }	{ 1,02 }	0 { , 101 ,1212}	{0101, 2 , 121 }
Orbifold		4*3	6*2	2*32	2*33	3*22
Bezpośrednie podgrupy
Indeks	2	4			8
Diagram
Coxeter	[6,4] + =	[6,4 + ] + =	[6 + ,4] + =	[(6,4,2 + )] + =	[6 + ,4 + ] + = [1 + ,6,1 + ,4,1 + ] = = =
Generatory	{01,12}	{(01) 2 ,12}	{01,(12) 2 }	{02,(01) 2 ,(12) 2 }	{(01) 2 ,(12) 2 ,2(01) 2 2}
Orbifold	642	443	662	3222	3232
Radykalne podgrupy
Indeks		8	12	16	24
Diagram
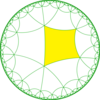
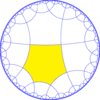
Coxeter		[6,4*] =	[6*,4]	[6,4*] + =	[6*,4] +
Orbifold		*3333	*222222	3333	222222

Zobacz też

• Tilings regularnych wielokątów
• Lista jednolitych nachyleń planarnych

•   John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Rozdział 19, Hiperboliczne mozaiki Archimedesa)
•    „Rozdział 10: Regularne plastry miodu w przestrzeni hiperbolicznej”. Piękno geometrii: dwanaście esejów . Publikacje Dover. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .

Linki zewnętrzne

• Weisstein, Eric W. „Dachówka hiperboliczna” . MathWorld .
• Weisstein, Eric W. „Dysk hiperboliczny Poincarégo” . MathWorld .
• Galeria płytek hiperbolicznych i sferycznych
• KaleidoTile 3: Oprogramowanie edukacyjne do tworzenia nachyleń sferycznych, płaskich i hiperbolicznych
• Hiperboliczne płaskie mozaiki, Don Hatch