Płytki Girih

Płytki Girih
Wzorzyste płytki Girih
Linie konstrukcyjne są zazwyczaj ukryte: po lewej płytki geometryczne, po prawej wzór girih .

Płytki Girih to zestaw pięciu płytek , które zostały użyte do stworzenia islamskich wzorów geometrycznych przy użyciu plecionki ( girih ) do dekoracji budynków w architekturze islamu . Były używane od około 1200 roku, a ich aranżacje uległy znacznej poprawie, począwszy od Darb-i Imam w Isfahanie w Iranie , zbudowanej w 1453 roku.

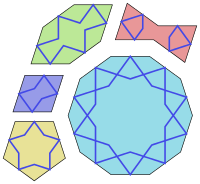
Pięć płytek

Pięć kształtów płytek i ich perskie nazwy to:

  • regularny dziesięciokąt z dziesięcioma wewnętrznymi kątami 144 °, Tabl ;
  • wydłużony (nieregularny wypukły) sześciokąt o kątach wewnętrznych 72°, 144°, 144°, 72°, 144°, 144°, Shesh Band ;
  • muszka (sześciokąt niewypukły) o kątach wewnętrznych 72°, 72°, 216°, 72°, 72°, 216°, Sormeh Dan ;
  • romb o kątach wewnętrznych 72°, 108°, 72°, 108° , Torange ; I
  • regularny pięciokąt z pięcioma wewnętrznymi kątami 108 °, Pange .

Wszystkie boki tych figur mają taką samą długość, a wszystkie ich kąty są wielokrotnościami 36° (π/5 radianów ). Wszystkie z wyjątkiem pięciokąta mają dwustronną (odbiciową) symetrię przez dwie prostopadłe linie. Niektóre mają dodatkowe symetrie. W szczególności dziesięciokąt ma dziesięciokrotną symetrię obrotową (obrót o 36 °); a pięciokąt ma pięciokrotną symetrię obrotową (obrót o 72 °).

Pojawienie się płytek girih

Pod koniec XI wieku muzułmańscy artyści w Afryce Północnej zaczęli używać „ mozaiki kafelkowej ”, która jest poprzedniczką teselacji . W XIII wieku islamiści odkryli nowy sposób konstruowania „mozaiki kafelkowej” dzięki rozwojowi obliczeń arytmetycznych i geometrii — kafelki girih.

Girih

Główny artykuł: Girih

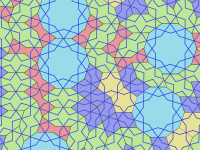
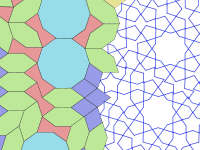
Girih to linie ( plecionki ), które zdobią płytki. Płytki są używane do tworzenia wzorów girih, od perskiego słowa گره , oznaczającego „węzeł”. W większości przypadków widoczne są tylko girih (i inne drobne dekoracje, takie jak kwiaty), a nie granice samych płytek. Girih to podzielone na kawałki linie proste, które przecinają granice płytek w środku krawędzi pod kątem 54 ° (3π/10 radianów) do krawędzi. Dwa przecinające się girih przecinają każdą krawędź płytki. Większość płytek ma unikalny wzór girih wewnątrz płytki, który jest ciągły i zgodny z symetrią płytki. Jednak dziesięciokąt ma dwa możliwe wzory girih, z których jeden ma tylko pięciokrotną, a nie dziesięciokrotną symetrię obrotową.

Matematyka Tilings Girih

W 2007 roku fizycy Peter J. Lu i Paul J. Steinhardt zasugerowali, że nachylenia girih mają właściwości zgodne z samopodobnymi fraktalnymi kwazikrystalicznymi nachyleniami, takimi jak nachylenia Penrose'a , wyprzedzając je o pięć stuleci.

Odkrycie to zostało poparte zarówno analizą wzorów na zachowanych konstrukcjach, jak i badaniem perskich zwojów z XV wieku. Nic nie wskazuje na to, o ile więcej architekci mogli wiedzieć na temat matematyki. Powszechnie uważa się, że takie projekty były konstruowane przez rysowanie zygzakowatych konturów tylko za pomocą liniału i kompasu. Być może korzystano z szablonów znalezionych na zwojach, takich jak zwój Topkapi o długości 97 stóp (29,5 metra) . Znajduje się w Pałacu Topkapi w Stambule, centrum administracyjnym Imperium Osmańskiego, datowany prawdopodobnie na koniec XV wieku, zwój przedstawia ciąg dwu- i trójwymiarowych wzorów geometrycznych. Nie ma tekstu, ale jest wzór siatki i kodowanie kolorami używane do podkreślenia symetrii i rozróżnienia trójwymiarowych projekcji. Rysunki, takie jak pokazane na tym zwoju, służyły jako wzorce dla rzemieślników, którzy wytwarzali płytki, a kształty płytek girih dyktowały, w jaki sposób można je łączyć w duże wzory. W ten sposób rzemieślnicy mogli tworzyć bardzo złożone projekty bez uciekania się do matematyki i niekoniecznie rozumienia ich podstawowych zasad.

To wykorzystanie powtarzających się wzorów utworzonych z ograniczonej liczby kształtów geometrycznych dostępnych dla ówczesnych rzemieślników jest podobne do praktyki współczesnych europejskich rzemieślników gotyckich . Projektantom obu stylów zależało na wykorzystaniu swoich inwentarzy geometrycznych kształtów do stworzenia maksymalnej różnorodności form. Wymagało to umiejętności i praktyki bardzo różniących się od matematyki.

Geometryczna konstrukcja zazębiającego się wzoru mozaiki dekagram-wielokąt

Najpierw podziel kąt prosty A na pięć części tego samego stopnia, tworząc cztery promienie wychodzące z punktu A. Znajdź dowolny punkt C na drugim półprostym i opuść prostopadłe z punktu C na boki kąta A w kierunku przeciwnym do ruchu wskazówek zegara. Ten krok tworzy prostokąt ABCD wraz z czterema segmentami, z których każdy ma punkt końcowy w punkcie A; inne punkty końcowe to przecięcia czterech promieni z dwoma bokami BC i DC prostokąta ABCD. Następnie znajdź środek czwartego odcinka utworzonego z czwartego punktu E. Skonstruuj łuk o środku A i promieniu AE, który przecina AB w punkcie F i drugą półprostą w punkcie G. Drugi odcinek jest teraz częścią prostokąta przekątna. Poprowadź linię równoległą do AD i przechodzącą przez punkt G, która przecina pierwszą półprostą w punkcie H i trzecią półprostą w punkcie I. Prosta HF przechodzi przez punkt E i przecina trzecią półprostą w punkcie L i prostą AD w punkcie J. Skonstruuj prostą przechodzącej przez J, która jest równoległa do trzeciego promienia. Skonstruuj również prostą EI i znajdź M, które jest przecięciem tej prostej z AD. Z punktu F poprowadź linię równoległą do trzeciej półprostej, aby przecięła pierwszą półprostą w punkcie K. Skonstruuj odcinki GK, GL i EM. Znajdź punkt N taki, że GI = IN, konstruując okrąg o środku I i promieniu IG. Skonstruuj linię DN, która jest równoległa do GK, aby przecinała linię wychodzącą z J i znajdź P, aby uzupełnić pięciokąt foremny EINPJ. Linia DN przecina prostopadłą dwusieczną AB w punkcie Q. Z punktu Q skonstruuj linię równoległą do FK do przecięcia z promieniem MI w punkcie R. Jak pokazano na rysunku, używając punktu O, który jest środkiem prostokąta ABCD, jako środka obrotu o 180° , można utworzyć podstawowy region dla płytek.

Zazębiająca się mozaika dekagramowo-wielokątna
Zazębiająca się mozaika dekagramowo-wielokątna
Zazębiająca się mozaika dekagramowo-wielokątna
Zazębiająca się mozaika dekagramowo-wielokątna

Geometryczna konstrukcja teselacji ze zwojów architektonicznych Mirzy Akbar

Najpierw podziel kąt prosty na pięć przystających kątów. Dowolny punkt P jest wybrany na pierwszym promieniu przeciwnie do ruchu wskazówek zegara. Dla promienia okręgu wpisanego w dekagram wybrano połowę odcinka utworzonego z trzeciego promienia, segment AM. Poniższy rysunek ilustruje krok po kroku wizualne rozwiązanie problemu przez autora. Zwróć uwagę, że sposób podziału kąta prostego na pięć kątów przystających nie jest częścią instrukcji, ponieważ jest uważany za elementarny krok dla projektantów.

Krok po kroku konstrukcja kompasowo-liniowa teselacji

Przykłady

Girih był szeroko stosowany w architekturze. Girih na perskich geometrycznych oknach spełniają wymagania perskiej architektury. Specyficzne rodzaje ozdób stosowanych w orosi zazwyczaj łączyły okna ze społeczną i polityczną dominacją patrona. Im bardziej ozdobne jest okno, tym wyższy status społeczny i ekonomiczny ma właściciel. Dobrym tego przykładem jest Azad Koliji, ogród Dowlatabad w Iranie [ potrzebne źródło ] . Wzory girih na jego oknie z powodzeniem demonstrują wiele warstw. Pierwszą warstwą byłby rzeczywisty ogród, na który ludzie mogą rzucić okiem, otwierając okno. Następnie jest pierwszy wzór girih na zewnętrznej stronie okna, rzeźbiony wzór. Kolejną sztuczną warstwę stanowi kolorowe szkło okna, którego wielobarwne warstwy tworzą wrażenie masy kwiatów. Ta abstrakcyjna warstwa stanowi wyraźną sprzeczność z realną warstwą za oknem i daje pole do popisu wyobraźni.

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Girih_tiles&oldid=1135176891 ”