Zamówienie-4 pięciokątne kafelki

Porządek-4 pięciokątny kafelkowy
Order-4 pentagonal tiling
model dysku Poincarégo płaszczyzny hiperbolicznej
Typ Hiperboliczne regularne kafelkowanie
Konfiguracja wierzchołków 5 4
Symbol Schläfliego
{5,4} r {5,5} lub
Symbol Wythoffa
4 | 5 2 2 | 5 5
Diagram Coxetera CDel node 1.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node.png
CDel node.pngCDel 5.pngCDel node 1.pngCDel 5.pngCDel node.pngLubCDel node 1.pngCDel split1-55.pngCDel nodes.png
Grupa symetrii
[5,4], (*542) [5,5], (*552)
Podwójny Zamówienie-5 kwadratowych płytek
Nieruchomości Vertex-przechodnie , krawędzie-przechodnie , ściany-przechodnie

W geometrii pięciokątne układanie rzędu 4 jest regularnym układaniem płaszczyzny hiperbolicznej . Ma symbol Schläfliego {5,4}. Można to również nazwać pięciopięciokątną płytką w dwukolorowej quasiregularnej formie.

Symetria

Ta płytka przedstawia hiperboliczny kalejdoskop 5 luster spotykających się jako krawędzie pięciokąta foremnego. Ta symetria w notacji orbifold nazywa się * 22222 z 5 przecięciami lustrzanymi rzędu 2. W notacji Coxetera można przedstawić jako [5 * ,4], usuwając dwa z trzech zwierciadeł (przechodzących przez środek pięciokąta) w symetrii [5,4].

Domeny kalejdoskopowe można postrzegać jako dwukolorowe pięciokąty, reprezentujące lustrzane odbicia domeny podstawowej. Kolorystyka ta reprezentuje ułożenie jednolite t 1 {5,5} i jako ułożenie quasiregularne nazywane jest ułożeniem pentapentagonalnym .

Uniform tiling 552-t1.png

Powiązane wielościany i kafelkowanie

Jednolite płytki pięciokątne / kwadratowe
Symetria: [5,4], (*542) [5,4] + , (542) [5 + ,4], (5*2) [5,4,1 + ], (*552)
CDel node 1.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node.png CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 4.pngCDel node.png CDel node.pngCDel 5.pngCDel node 1.pngCDel 4.pngCDel node.png CDel node.pngCDel 5.pngCDel node 1.pngCDel 4.pngCDel node 1.png CDel node.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node 1.png CDel node 1.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node 1.png CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 4.pngCDel node 1.png CDel node h.pngCDel 5.pngCDel node h.pngCDel 4.pngCDel node h.png CDel node h.pngCDel 5.pngCDel node h.pngCDel 4.pngCDel node.png CDel node.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node h.png
H2-5-4-dual.svg H2-5-4-trunc-dual.svg H2-5-4-rectified.svg H2-5-4-trunc-primal.svg H2-5-4-primal.svg H2-5-4-cantellated.svg H2-5-4-omnitruncated.svg H2-5-4-snub.svg Uniform tiling 542-h01.png Uniform tiling 552-t0.png
{5,4} t{5,4} r{5,4} 2t{5,4}=t{4,5} 2r{5,4}={4,5} rrr{5,4} tr{5,4} sr{5,4} s{5,4} h{4,5}
Jednolite dublety
CDel node f1.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node.png CDel node f1.pngCDel 5.pngCDel node f1.pngCDel 4.pngCDel node.png CDel node.pngCDel 5.pngCDel node f1.pngCDel 4.pngCDel node.png CDel node.pngCDel 5.pngCDel node f1.pngCDel 4.pngCDel node f1.png CDel node.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node f1.png CDel node f1.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node f1.png CDel node f1.pngCDel 5.pngCDel node f1.pngCDel 4.pngCDel node f1.png CDel node fh.pngCDel 5.pngCDel node fh.pngCDel 4.pngCDel node fh.png CDel node fh.pngCDel 5.pngCDel node fh.pngCDel 4.pngCDel node.png CDel node.pngCDel 5.pngCDel node.pngCDel 4.pngCDel node fh.png
H2-5-4-primal.svg H2-5-4-kis-primal.svg H2-5-4-rhombic.svg H2-5-4-kis-dual.svg H2-5-4-dual.svg H2-5-4-deltoidal.svg H2-5-4-kisrhombille.svg H2-5-4-floret.svg Uniform tiling 552-t2.png
V5 4 V4.10.10 V4.5.4.5 V5.8.8 V4 5 V4.4.5.4 V4.8.10 V3.3.4.3.5 V3.3.5.3.5 V5 5
Jednolite pięciopięciokątne nachylenia
Symetria: [5,5], (*552) [5,5] + , (552)
CDel node 1.pngCDel 5.pngCDel node.pngCDel 5.pngCDel node.png
=CDel node h1.pngCDel 4.pngCDel node.pngCDel 5.pngCDel node.png 		CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 5.pngCDel node.png
=CDel node h1.pngCDel 4.pngCDel node.pngCDel 5.pngCDel node 1.png 		CDel node.pngCDel 5.pngCDel node 1.pngCDel 5.pngCDel node.png
=CDel node h0.pngCDel 4.pngCDel node.pngCDel 5.pngCDel node 1.png 		CDel node.pngCDel 5.pngCDel node 1.pngCDel 5.pngCDel node 1.png
=CDel node h1.pngCDel 4.pngCDel node.pngCDel 5.pngCDel node 1.png 		CDel node.pngCDel 5.pngCDel node.pngCDel 5.pngCDel node 1.png
=CDel node h1.pngCDel 4.pngCDel node.pngCDel 5.pngCDel node.png 		CDel node 1.pngCDel 5.pngCDel node.pngCDel 5.pngCDel node 1.png
=CDel node h0.pngCDel 4.pngCDel node 1.pngCDel 5.pngCDel node.png 		CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 5.pngCDel node 1.png
=CDel node h0.pngCDel 4.pngCDel node 1.pngCDel 5.pngCDel node 1.png 		CDel node h.pngCDel 5.pngCDel node h.pngCDel 5.pngCDel node h.png
=CDel node h0.pngCDel 4.pngCDel node h.pngCDel 5.pngCDel node h.png
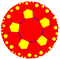
Uniform tiling 552-t0.png Uniform tiling 552-t01.png Uniform tiling 552-t1.png Uniform tiling 552-t12.png Uniform tiling 552-t2.png Uniform tiling 552-t02.png Uniform tiling 552-t012.png Uniform tiling 552-snub.png

Kolejność-5 pięciokątnych kafelków {5,5}
Obcięte zamówienie - 5 pięciokątnych kafelków t{5,5}
Kolejność-4 pięciokątne kafelki r{5,5}
Porządek obcięty - 5 pięciokątnych kafelków 2t{5,5} = t{5,5}
Kolejność-5 pięciokątnych kafelków 2r{5,5} = {5,5}
Kafelki czworokątne rr{5,5}
Obcięte zamówienie - 4 pięciokątne kafelki tr{5,5}
Zadarta pięciokątna dachówka sr{5,5}
Jednolite dublety
CDel node f1.pngCDel 5.pngCDel node.pngCDel 5.pngCDel node.png CDel node f1.pngCDel 5.pngCDel node f1.pngCDel 5.pngCDel node.png CDel node.pngCDel 5.pngCDel node f1.pngCDel 5.pngCDel node.png CDel node.pngCDel 5.pngCDel node f1.pngCDel 5.pngCDel node f1.png CDel node.pngCDel 5.pngCDel node.pngCDel 5.pngCDel node f1.png CDel node f1.pngCDel 5.pngCDel node.pngCDel 5.pngCDel node f1.png CDel node f1.pngCDel 5.pngCDel node f1.pngCDel 5.pngCDel node f1.png CDel node fh.pngCDel 5.pngCDel node fh.pngCDel 5.pngCDel node fh.png
Uniform tiling 552-t2.png Order5 pentakis pentagonal til.png H2-5-4-primal.svg Order5 pentakis pentagonal til.png Uniform tiling 552-t0.png H2-5-4-rhombic.svg H2-5-4-kis-primal.svg

Zamówienie-5 pięciokątnych płytek V5.5.5.5.5 		V5.10.10
Zamówienie-5 kwadratowych płytek V5.5.5.5 		V5.10.10
Zamówienie-5 pięciokątnych płytek V5.5.5.5.5 		V4.5.4.5 V4.10.10 V3.3.5.3.5

CDel node 1.pngCDel 5.pngCDel node.pngCDel n.pngCDel node.png To kafelkowanie jest powiązane topologicznie jako część sekwencji wielościanów foremnych i kafelków o ścianach pięciokątnych , zaczynając od dwunastościanu , z symbolem Schläfliego {5,n} i diagramu Coxetera , idąc do nieskończoności.

CDel node 1.pngCDel n.pngCDel node.pngCDel 4.pngCDel node.png To kafelkowanie jest również powiązane topologicznie jako część sekwencji regularnych wielościanów i kafelków z czterema ścianami na wierzchołek, zaczynając od ośmiościanu , z symbolem Schläfliego {n,4} i diagramem Coxetera , gdzie n dąży do nieskończoności.

* n 42 mutacja symetrii regularnych nachyleń: { n ,4}
Kulisty euklidesowy Nachylenia hiperboliczne
Spherical square hosohedron.png Spherical square bipyramid.svg Uniform tiling 44-t0.svg H2-5-4-dual.svg H2 tiling 246-1.png H2 tiling 247-1.png H2 tiling 248-1.png H2 tiling 24i-1.png
2 4 3 4 4 4 5 4 6 4 7 4 8 4 ... ∞ 4

To kafelkowanie jest topologicznie powiązane jako część ciągu wielościanów foremnych i kafelków z figurą wierzchołkową (4 n ).

* n 42 mutacja symetrii regularnych nachyleń: {4, n }
Kulisty euklidesowy Kompaktowy hiperboliczny Parakompaktowy
Uniform tiling 432-t0.png
{4,3}
CDel node 1.pngCDel 4.pngCDel node.pngCDel 3.pngCDel node.png 		Uniform tiling 44-t0.svg
{4,4}
CDel node 1.pngCDel 4.pngCDel node.pngCDel 4.pngCDel node.png 		H2-5-4-primal.svg
{4,5}
CDel node 1.pngCDel 4.pngCDel node.pngCDel 5.pngCDel node.png 		H2 tiling 246-4.png
{4,6}
CDel node 1.pngCDel 4.pngCDel node.pngCDel 6.pngCDel node.png 		H2 tiling 247-4.png
{4,7}
CDel node 1.pngCDel 4.pngCDel node.pngCDel 7.pngCDel node.png 		H2 tiling 248-4.png
{4,8} ...
CDel node 1.pngCDel 4.pngCDel node.pngCDel 8.pngCDel node.png 		H2 tiling 24i-4.png
{4,∞}
CDel node 1.pngCDel 4.pngCDel node.pngCDel infin.pngCDel node.png
*5 n 2 mutacje symetrii quasiregularnych nachyleń: (5.n) 2


Symetria *5 n 2 [n,5] 		Kulisty Hiperboliczny Parakompaktowy Niekompaktowy

*352 [3,5]
*452 [4,5]
*552 [5,5]
*652 [6,5]
*752 [7,5]
*852 [8,5]...
*∞52 [∞,5] 		 
[ n i,5]
Figurki Uniform tiling 532-t1.png H2-5-4-rectified.svg H2 tiling 255-2.png H2 tiling 256-2.png H2 tiling 257-2.png H2 tiling 258-2.png H2 tiling 25i-2.png
Konfig. (5.3) 2 (5.4) 2 (5.5) 2 (5.6) 2 (5.7)2 (5.8)2 (5.∞) 2 (5. n ja) 2

Rombowe figury 		Rhombictriacontahedron.jpg H2-5-4-rhombic.svg H2-5-4-primal.svg Order-6-5 quasiregular rhombic tiling.png
Konfig. V(5.3) 2 V(5.4) 2 V(5.5) 2 V(5.6) 2 V(5.7) 2 V(5.8) 2 V(5.∞) 2 V(5.∞) 2
  •   John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Rozdział 19, Hiperboliczne mozaiki Archimedesa)
  •    Coxeter, HSM (1999), rozdział 10: Regularne plastry miodu w przestrzeni hiperbolicznej (PDF) , The Beauty of Geometry: Twelve Essays , Dover Publications, ISBN 0-486-40919-8 , LCCN 99035678 , wykład na zaproszenie, ICM, Amsterdam, 1954 .

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Order-4_pentagonal_tiling&oldid=1015273436 ”