Ośmiokątna dachówka kantykowa
| Kantyczny ośmiokątny | |
|---|---|
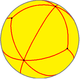
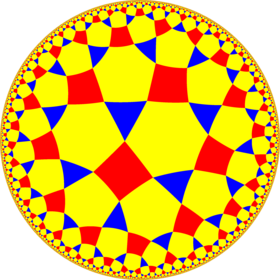 model dysku Poincarégo płaszczyzny hiperbolicznej |
|
| Typ | Hiperboliczne jednolite kafelkowanie |
| Konfiguracja wierzchołków | 3.6.4.6 |
| Symbol Schläfliego | godz. 2 {8,3} |
| Symbol Wythoffa | 4 3 | 3 |
| Diagram Coxetera |
|
| Grupa symetrii | [(4,3,3)], (*433) |
| Podwójny | Zamówienie-4-3-3 t12 podwójne kafelkowanie |
| Nieruchomości | Przechodnie wierzchołków |
W geometrii płytki tritetratrygonalne lub płytki shieldotritetragonal są jednolitymi płytkami płaszczyzny hiperbolicznej . Ma symbol Schläfliego t 1,2 (4,3,3). Można go również nazwać dachówką ośmiokątną skośną , h 2 {8,3}.
Podwójne układanie płytek
Powiązane wielościany i kafelkowanie
| Jednolite (4,3,3) nachylenia | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symetria: [(4,3,3)], (*433) | [(4,3,3)] + , (433) | ||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||

|

|

|

|

|

|

|

|
||||
|
0 h{8,3} t (4,3,3) |
r{3,8} 1 / 2 t 0,1 (4,3,3) |
h{8,3} t 1 (4,3,3) |
godz 2 {8,3} t 1,2 (4,3,3) |
{3,8} 1 / 2 t 2 (4,3,3) |
godz 2 {8,3} t 0,2 (4,3,3) |
t{3,8} 1 / 2 t 0,1,2 (4,3,3) |
s{3,8} 1 / 2 s(4,3,3) |
||||
| Jednolite dublety | |||||||||||

|

|

|

|

|

|

|

|
||||
| V(3.4) 3 | V3.8.3.8 | V(3.4) 3 | V3.6.4.6 | V(3.3) 4 | V3.6.4.6 | Wersja 6.6.8 | V3.3.3.3.3.4 | ||||
|
Symetria *n32 [1 + ,2n,3] = [(n,3,3)] |
Kulisty | euklidesowy | Kompaktowy hiperboliczny | Parakompaktowy | ||
|---|---|---|---|---|---|---|
|
*233 [1 + ,4,3] = [3,3] |
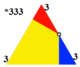
*333 [1 + ,6,3] = [(3,3,3)] |
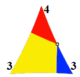
*433 [1 + ,8,3] = [(4,3,3)] |
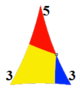
*533 [1 + ,10,3] = [(5,3,3)] |
*633... [1 + ,12,3] = [(6,3,3)] |
*∞33 [1 + ,∞,3] = [(∞,3,3)] |
|
|
Coxeter Schläfli |
= h 2 {4,3} |
= godz 2 {6,3} |
= h 2 {8,3} |
= h2 { 10,3} |
= h2 { 12,3} |
= h 2 {∞,3} |
| Postać kantycka |

|

|

|

|

|

|
| Wierzchołek | 3.6. 2.6 _ | 3.6. 3 .6 | 3.6. 4 .6 | 3.6.5.6 | 3.6.6.6 | 3.6.∞.6 |
 Domena |

|
|
|
|

|

|
| Wythoffa | 2 3 | 3 | 3 3 | 3 | 4 3 | 3 | 5 3 | 3 | 6 3 | 3 | ∞ 3 | 3 |
|
Podwójna postać |
|

|

|
|||
| Twarz | V3.6.2.6 | V3.6.3.6 | V3.6.4.6 | V3.6.5.6 | V3.6.6.6 | V3.6.∞.6 |
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Rozdział 19, Hiperboliczne mozaiki Archimedesa)
- „Rozdział 10: Regularne plastry miodu w przestrzeni hiperbolicznej”. Piękno geometrii: dwanaście esejów . Publikacje Dover. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
Zobacz też
Linki zewnętrzne
- Weisstein, Eric W. „Dachówka hiperboliczna” . MathWorld .
- Weisstein, Eric W. „Dysk hiperboliczny Poincarégo” . MathWorld .
- Galeria płytek hiperbolicznych i sferycznych
- KaleidoTile 3: Oprogramowanie edukacyjne do tworzenia nachyleń sferycznych, płaskich i hiperbolicznych
- Hiperboliczne płaskie mozaiki, Don Hatch


