Potencjalny przepływ wokół okrągłego cylindra

W matematyce przepływ potencjalny wokół okrągłego cylindra jest klasycznym rozwiązaniem przepływu nielepkiego , nieściśliwego płynu wokół cylindra, który jest poprzeczny do przepływu . Daleko od cylindra przepływ jest jednokierunkowy i równomierny. Przepływ nie ma wirowości , dlatego pole prędkości jest bezwirowe i można je modelować jako przepływ potencjalny . W przeciwieństwie do prawdziwego płynu, rozwiązanie to wskazuje zerowy opór netto na ciele, wynik znany jako paradoks d'Alemberta .

Rozwiązanie matematyczne

Kolory: pole ciśnieniowe. Czerwony jest wysoki, a niebieski niski. Wektory prędkości.

Zbliżenie jednej ćwiartki przepływu. Kolory: pole ciśnieniowe. Czerwony jest wysoki, a niebieski niski. Wektory prędkości.

Pole ciśnienia (kolory), funkcja strumienia ( czarny ) z odstępem konturowym 0,2 Ur od dołu do góry, potencjał prędkości ( biały ) z odstępem konturowym 0,2 Ur od lewej do prawej.

Cylinder (lub dysk) o promieniu R umieszczony jest w dwuwymiarowym, nieściśliwym i nielepkim przepływie. Celem jest znalezienie ustalonego wektora prędkości V i ciśnienia p w płaszczyźnie, pod warunkiem, że z dala od cylindra wektor prędkości (względem wektorów jednostkowych i oraz j ) wynosi:

${\ Displaystyle \ mathbf {V} = U \ mathbf {i} +0 \ mathbf {j} \,,}$

gdzie U jest stałą i na granicy walca

${\ Displaystyle \ mathbf {V} \ cdot \ mathbf {\ kapelusz {n}} = 0 \,,}$

gdzie n̂ jest wektorem normalnym do powierzchni cylindra. Przepływ w górę rzeki jest równomierny i nie ma wirowości. Przepływ jest nielepki, nieściśliwy i ma stałą gęstość masy ρ . Dlatego przepływ pozostaje bez wirowości lub mówi się, że jest bezwirowy , gdzie ∇ × V = 0 wszędzie. Ponieważ jest on nierotacyjny, musi istnieć potencjał prędkości φ :

${\ Displaystyle \ mathbf {V} = \ nabla \ phi \,.}$

Będąc nieściśliwym, ∇ · V = 0 , więc φ musi spełniać równanie Laplace'a :

${\ Displaystyle \ nabla ^ {2} \ phi = 0 \,.}$

Rozwiązanie dla φ najłatwiej uzyskać we współrzędnych biegunowych r i θ , odniesionych do konwencjonalnych współrzędnych kartezjańskich przez x = r cos θ i y = r sin θ . We współrzędnych biegunowych równanie Laplace'a wygląda następująco (patrz Del we współrzędnych cylindrycznych i sferycznych ):

${\ Displaystyle {\ Frac {1} {r}} {\ Frac {\ częściowy}} \frac {1} {r^{2}}} {\frac {\częściowe ^{2}\phi }\częściowe \theta ^{2}}}=0\,.}$

Rozwiązanie spełniające warunki brzegowe to

${\ Displaystyle \ phi (r, \ teta) = Ur \ lewo (1 + {\ Frac {R ^ {2}} {r ^ {2}}} \ prawo) \ cos \ theta \,.}$

Składowe prędkości we współrzędnych biegunowych wyznacza się ze składowych ∇ φ we współrzędnych biegunowych:

${\ Displaystyle V_ {r} = {\ Frac {\ częściowe \ phi} {\ częściowe r}} = U \ lewo (1- {\frac {R^{2}}{r^{2}}}\right)\cos \theta }$

I

${\ Displaystyle V _ {\ teta} = {\ Frac {1} {r}} {\ Frac {\ częściowe \ phi} {\ częściowe \ theta}} = - U \ lewo (1 + {\ Frac {R ^ { 2}}{r^{2}}}\right)\sin \theta \,.}$

Będąc nielepkim i nierotacyjnym, równanie Bernoulliego pozwala uzyskać rozwiązanie pola ciśnienia bezpośrednio z pola prędkości:

${\ Displaystyle p = {\ tfrac {1} {2}} \ rho \ lewo (U ^ {2} -V ^ {2} \ prawo) +p_{\infty},}$

gdzie stałe U i p _∞ pojawiają się tak, że p → p _∞ daleko od cylindra, gdzie V = U . Używając V ² = V
² _r + V
² _θ ,

${\ Displaystyle p = {\ tfrac {1}}} )-{\frac {R^{4}}{r^{4}}}\right)+p_{\infty}\,.}$

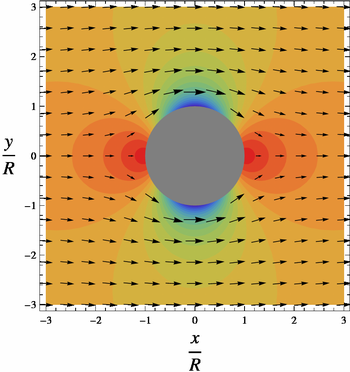
Na rysunkach pokolorowane pole zwane „ciśnieniem” jest wykresem

${\ Displaystyle 2 {\ Frac {p-p _ {\ infty}} {\ rho U ^ {2}}} = 2 {\ Frac {R ^ {2}} \theta )-{\frac {R^{4}}{r^{4}\,}}.}$

Na powierzchni cylindra, czyli r = R , ciśnienie zmienia się od maksymalnie 1 (pokazane na wykresie na czerwono ) w punktach stagnacji przy θ = 0 i θ = π do minimum -3 (pokazane na niebiesko ) po bokach cylindra, przy θ = π / 2 i θ = 3π / 2 . Podobnie V zmienia się od V = 0 w punktach stagnacji do V = 2 U po bokach, przy niskim ciśnieniu.

Funkcja strumienia

Ponieważ przepływ jest nieściśliwy, można znaleźć funkcję strumienia taką, że

${\ Displaystyle \ mathbf {V} = \ nabla \ psi \ razy \ mathbf {k} \,.}$

Z tej definicji wynika, używając tożsamości wektorowych ,

${\ Displaystyle \ mathbf {V} \ cdot \ nabla {\ psi} = 0 \,.}$

Zatem kontur o stałej wartości ψ będzie także linią prądu, czyli linią styczną do V . Dla przepływu przez cylinder znajdujemy:

${\ Displaystyle \ psi = U \ lewo (r - {\ Frac {R ^ {2}} {r}} \ prawo) \ grzech \ theta \,.}$

Interpretacja fizyczna

Równanie Laplace'a jest liniowe i jest jednym z najbardziej elementarnych równań różniczkowych cząstkowych . To proste równanie daje całe rozwiązanie zarówno dla V , jak i p ze względu na ograniczenie irracjonalności i nieściśliwości. Po otrzymaniu rozwiązania dla V i p można zauważyć zgodność gradientu ciśnienia z przyspieszeniami.

Ciśnienie dynamiczne w wartość 1/2 ρU ² górnym punkcie stagnacji ma . wartość potrzebna do wyhamowania swobodnego przepływu strumienia o prędkości U . Ta sama wartość pojawia się w punkcie stagnacji za rurociągiem; to wysokie ciśnienie jest ponownie potrzebne do spowolnienia przepływu do prędkości zerowej. Ta symetria powstaje tylko dlatego, że przepływ jest całkowicie pozbawiony tarcia.

dośrodkowe przyspieszenie przepływu, potrzebne jest niskie ciśnienie po bokach cylindra :

${\ Displaystyle {\ Frac {\ częściowe p} {\ częściowe r}} = {\ Frac {\ rho V ^ {2}} {L}} \,,}$

gdzie L jest promieniem krzywizny przepływu. Ale L ≈ R i V ≈ U . W ten sposób otrzymamy całkę z równania przyspieszenia dośrodkowego na odległość Δ r ≈ R

${\ Displaystyle p-p _ {\ infty} \ około - \ rho U ^ {2} \,.}$

Dokładne rozwiązanie ma, dla najniższego ciśnienia,

${\ Displaystyle p-p _ {\ infty} = - {\ tfrac {3} {2}} \ rho U ^ {2} \,.}$

Niskie ciśnienie, które musi być obecne, aby zapewnić przyspieszenie dośrodkowe, również zwiększy prędkość przepływu, gdy płyn przemieszcza się od wyższych do niższych wartości ciśnienia. W ten sposób znajdujemy maksymalną prędkość przepływu, V = 2 U , przy niskim ciśnieniu po bokach cylindra.

Wartość V > U jest zgodna z zasadą zachowania objętości płynu. Gdy cylinder blokuje część przepływu, V musi być większe niż U gdzieś w płaszczyźnie przechodzącej przez środek cylindra i poprzecznie do przepływu.

Porównanie z przepływem prawdziwego płynu przez cylinder

Symetria tego idealnego rozwiązania ma punkt stagnacji zarówno z tyłu cylindra, jak i z przodu. Rozkład ciśnienia na przedniej i tylnej stronie jest identyczny, co prowadzi do szczególnej właściwości polegającej na zerowym oporze na cylindrze, właściwości znanej jako paradoks d'Alemberta . W przeciwieństwie do idealnego, nielepkiego płynu, lepki przepływ przez cylinder, niezależnie od tego, jak mała jest lepkość, nabierze cienkiej warstwy granicznej przylegającej do powierzchni cylindra. Nastąpi oddzielenie warstwy granicznej i powstanie śladu będzie istniał w przepływie za cylindrem. Ciśnienie w każdym punkcie po stronie cylindra będzie niższe niż po stronie wlotowej, co spowoduje powstanie siły oporu w kierunku dolnym.

Ekspansja Janzena – Rayleigha

Problem potencjalnego ściśliwego przepływu przez okrągły cylinder został po raz pierwszy zbadany przez O. Janzena w 1913 r. i Lorda Rayleigha w 1916 r. z niewielkimi efektami ściśliwości. $_$ mały Macha _ gdzie c jest prędkością dźwięku . Zatem rozwiązaniem przybliżenia pierwszego rzędu pod względem potencjału prędkości jest:

${\ Displaystyle \ phi (r, \ theta) = Ur \ lewo (1 + {\ Frac {a ^ {2}} {r ^ {2}}}\right)\cos \theta -\mathrm {M} ^{2}{\frac {Ur}{12}}\left[\left({\frac {13a^{2}}{r ^{2}}}-{\frac {6a^{4}}{r^{4}}}+{\frac {a^{6}}{r^{6}}}\right)\cos \ theta +\left({\frac {a^{4}}{r^{4}}}-{\frac {3a^{2}}{r^{2}}}\right)\cos 3\theta \right]+\mathrm {O} \left(\mathrm {M} ^{4}\right)\,}$

gdzie $jest$ cylindra.

Potencjalny przepływ przez okrągły cylinder z niewielkimi zmianami

Regularną analizę zaburzeń dla przepływu wokół cylindra z niewielkimi zaburzeniami w konfiguracjach można znaleźć w Milton Van Dyke (1975). Poniżej ε będzie reprezentować mały dodatni parametr, a a to promień walca. Bardziej szczegółowe analizy i dyskusje można znaleźć w książce Miltona Van Dyke'a z 1975 r. Perturbation Methods in Fluid Mechanics .

Lekko zdeformowany cylinder

Tutaj promień cylindra nie jest r = a , ale lekko zniekształconą formą r = a (1 - ε sin ² θ ) . Rozwiązaniem jest wówczas przybliżenie pierwszego rzędu

${\ Displaystyle \ psi (r, \ theta) = Ur \ lewo (1 - {\ Frac {a ^ {2}} {r ^ {2}}} \ prawo) \ grzech \ teta + \ varepsilon {\ frac { Ur} \sin 3\theta \right)+\mathrm {O} \left(\varepsilon ^{2}\right)}$

Lekko pulsujące kółko

Tutaj promień cylindra zmienia się nieznacznie w czasie, więc   r = a (1 + ε f ( t )) . Rozwiązaniem jest wówczas przybliżenie pierwszego rzędu

${\ Displaystyle \ psi (r, \ teta, t) = Ur \ lewo (1 - {\ Frac {a ^ {2}} {r ^ {2}}} \ prawo) \ sin \ theta + \varepsilon Ur\left({\frac {a^{2}}{Ur}}\theta f'(t)-{\frac {2a^{2}}{r^{2}}}f(t) \sin \theta \right)+\mathrm {O} \left(\varepsilon ^{2}\right)}$

Przepływ z lekką wirowością

Ogólnie rzecz biorąc, prędkość swobodnego strumienia U jest jednolita, innymi słowy ψ = Uy , ale tutaj na przepływ zewnętrzny narzucona jest niewielka wirowość.

Ścinanie liniowe

Tutaj wprowadza się liniowe ścinanie prędkości.

$początek {wyrównane} \ psi i = U \ lewo (y + { \frac {1}{2}}\varepsilon {\frac {y^{2}}{a}}\right)\,,\\[3pt]\omega &=-\nabla ^{2}\psi = -\varepsilon {\frac {U} {a}}\quad {\text{as}}x\rightarrow -\infty \,,\end{aligned}}}$

gdzie ε jest małym parametrem. Równanie rządzące jest następujące

${\ Displaystyle \ nabla ^ {2} \ psi = - \ omega (\ psi) \,.}$

Rozwiązaniem jest wówczas przybliżenie pierwszego rzędu

${\ Displaystyle \ psi (r, \ theta) = Ur \ lewo (1 - {\ Frac {a ^ {2}} {r ^ {2}}} \ prawo) \ grzech \ teta + \ varepsilon {\ frac { Ur} \theta -{\frac {a}}\right)+\mathrm {O} \left(\varepsilon ^{2}\right)\,.}$

Ścinanie paraboliczne

Wprowadzono tutaj ścinanie paraboliczne w prędkości zewnętrznej.

${\ Displaystyle {\ początek {wyrównane} \ psi i = U \ lewo (y + {\ tfrac {1} {6}} \ varepsilon {\ Frac {y ^ {3}} {a ^ {2}}} \ prawo )\,,\\\omega &=-\nabla ^{2}\psi =-\varepsilon U{\frac {y}{a^{2}}}\quad {\text{as }}x\rightarrow -\infty \,.\end{aligned}}}$

Rozwiązaniem jest wówczas przybliżenie pierwszego rzędu

${\ Displaystyle \ psi (r, \ theta) = Ur \ lewo (1 - {\ Frac {a ^ {2}} {r ^ {2}}} \ prawo) \ grzech \ teta + \ varepsilon {\ frac { Ur} +\mathrm {O} \left(\varepsilon ^{2}\right)\,,}$

gdzie χ jest jednorodnym rozwiązaniem równania Laplace'a, które przywraca warunki brzegowe.

Lekko porowaty cylinder

Niech C _ps oznacza współczynnik ciśnienia powierzchniowego nieprzepuszczalnego cylindra:

$_ {\ operatorname {ps}} = {\ Frac {p_ {s }-p_{\infty }}{{\tfrac {1}{2}}\rho U^{2}}}=1-4\sin ^{2}\theta =2\cos 2\theta -1\ ,,}$

gdzie p _s jest ciśnieniem powierzchniowym nieprzepuszczalnego cylindra. Niech teraz C _pi będzie współczynnikiem ciśnienia wewnętrznego wewnątrz cylindra, wówczas niewielka prędkość normalna wynikająca z niewielkiej porowatości wynika ze wzoru

${\ Displaystyle {\ Frac {1} {r}} {\ Frac {\ częściowe \ psi} {\ częściowe \ theta}} = \ varepsilon U \ lewo (C _ {\ operatorname {pi}} -C _ {\ operatorname { ps} }\right)=\varepsilon U\left(C_{\mathrm {pi} }+1-2\cos 2\theta \right)\quad {\text{at }}r=a\,,}$

ale warunek zerowego strumienia netto

${\ Displaystyle \ int _ {0} ^ {2 \ pi} {\ Frac {1} {r}} {\ Frac {\ częściowe \ psi} {\ częściowe \ theta }}\,\mathrm {d} \theta =0}$

wymaga, aby C _pi = −1 . Dlatego,

${\ Displaystyle {\ Frac {\ częściowe \ psi} {\ częściowe \ theta}} = -2 \ varepsilon rU \ cos 2 \ teta \ quad {\ tekst {w}} r = a \,.}$

Rozwiązaniem jest wówczas przybliżenie pierwszego rzędu

${\ Displaystyle \ psi (r, \ theta) = Ur \ lewo (1 - {\ Frac {a ^ {2}} {r ^ {2}}} \ prawo) \ sin \ theta - \ varepsilon U {\ Frac {a^{3}}{r^{2}}}\sin 2\theta +\mathrm {O} \left(\varepsilon ^{2}\right)\,.}$

Falisty quasi-cylinder

Jeżeli cylinder ma zmienny promień w kierunku osiowym, oś z , r = a ( 1 + ε sin z / b ) , to rozwiązaniem przybliżenia pierwszego rzędu pod względem trójwymiarowego potencjału prędkości jest

${\ Displaystyle \ phi (r, \ theta, z) = Ur \ lewo (1 + {\ Frac {a ^ {2}} {r ^ {2}}} \ prawo) \ cos \ teta -2 \ varepsilon Ub{\frac {K_{1}\left({\frac {r}}}\right)}{K_{1}'\left({\frac {r}}\right)}} \cos \theta \sin {\frac {z}{b}}+\mathrm {O} \left(\varepsilon ^{2}\right)\,,}$

gdzie K ₁ ( r / b ) jest zmodyfikowaną funkcją Bessela pierwszego rodzaju rzędu.

Zobacz też

• Transformacja Joukowsky’ego
• Stan Kutty
• Efekt Magnusa