Powierzchnia Richmonda

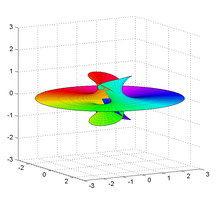
Powierzchnia Richmond dla m=2.

W geometrii różniczkowej powierzchnia Richmond jest minimalną powierzchnią opisaną po raz pierwszy przez Herberta Williama Richmonda w 1904 r. Jest to rodzina powierzchni z jednym płaskim końcem i jednym samoprzecinającym się końcem przypominającym powierzchnię Ennepera .

Ma parametryzację Weierstrassa-Ennepera ${\ Displaystyle f (z) = 1 / z ^ {2}, g (z) = z ^ {m}}$ . Pozwala to na parametryzację opartą na złożonym parametrze, takim jak

${\ Displaystyle {\ rozpocząć {wyrównane} X (z) i = \ Re [(-1/2z) -z ^ {2m + 1}/( 4m+2)]\\Y(z)&=\Re [(-i/2z)+iz^{2m+1}/(4m+2)]\\Z(z)&=\Re [z^ {m}/m]\end{wyrównane}}}$

Powiązana rodzina powierzchni to po prostu powierzchnia obrócona wokół osi Z.

Przyjmując m = 2, prawdziwe wyrażenie parametryczne przyjmuje postać:

${\ Displaystyle {\ rozpocząć {wyrównane} X (u, v) i = (1/3) u ^ {3} -uv ^ {2} + {\ Frac {u} {u ^ {2}+v^{2}}}\\Y(u,v)&=-u^{2}v+(1/3)v^{3}-{\frac {v}{u^{2 }+v^{2}}}\\Z(u,v)&=2u\end{wyrównane}}}$