Proces hierarchii analitycznej

Prosta hierarchia AHP z ostatecznymi priorytetami. Celem jest wybranie najbardziej odpowiedniego lidera spośród trzech kandydatów. Czynniki, które należy wziąć pod uwagę, to doświadczenie, wykształcenie, charyzma i wiek. Według osądów decydentów najsilniejszym kandydatem jest Dick, następnie Tom, a następnie Harry. Ich proces decyzyjny został szczegółowo opisany w załączniku do tego artykułu .

W teorii podejmowania decyzji analityczny proces hierarchiczny ( AHP ), także analityczny proces hierarchiczny , jest ustrukturyzowaną techniką organizowania i analizowania złożonych decyzji , opartą na matematyce i psychologii . Został opracowany przez Thomasa L. Saaty'ego w latach 70.; Saaty współpracował z Ernestem Formanem w celu opracowania Expert Choice w 1983 roku i od tego czasu firma AHP była intensywnie badana i udoskonalana. Reprezentuje dokładne podejście do ilościowego określania wag kryteriów decyzyjnych. poszczególnych ekspertów są wykorzystywane do oszacowania względnych wielkości czynników poprzez porównania parami. Każdy z respondentów porównuje względne znaczenie każdej pary pozycji za pomocą specjalnie zaprojektowanego kwestionariusza.

Zastosowania i zastosowania

AHP ma szczególne zastosowanie w grupowym podejmowaniu decyzji i jest używany na całym świecie w wielu różnych sytuacjach decyzyjnych , w dziedzinach takich jak rząd, biznes, przemysł, opieka zdrowotna i edukacja.

Zamiast zalecać „właściwą” decyzję, AHP pomaga decydentom znaleźć taką, która najlepiej odpowiada ich celowi i zrozumieniu problemu. Zapewnia kompleksowe i racjonalne ramy do strukturyzacji problemu decyzyjnego, do przedstawiania i kwantyfikowania jego elementów, do odnoszenia tych elementów do ogólnych celów oraz do oceny alternatywnych rozwiązań.

Użytkownicy AHP najpierw rozkładają swój problem decyzyjny na hierarchię łatwiejszych do zrozumienia podproblemów, z których każdy może być analizowany niezależnie. Elementy hierarchii mogą odnosić się do dowolnego aspektu problemu decyzyjnego — namacalnego lub niematerialnego, dokładnie zmierzonego lub z grubsza oszacowanego, dobrze lub źle zrozumianego — wszystkiego, co odnosi się do danej decyzji.

Po zbudowaniu hierarchii decydenci systematycznie oceniają jej różne elementy, porównując je ze sobą po dwa na raz, pod kątem ich wpływu na element znajdujący się wyżej w hierarchii. Dokonując porównań, decydenci mogą korzystać z konkretnych danych dotyczących elementów, ale zazwyczaj opierają się na swoich osądach dotyczących względnego znaczenia i ważności elementów. Istotą AHP jest to, że do przeprowadzania ocen można wykorzystać ludzkie osądy, a nie tylko podstawowe informacje.

AHP konwertuje te oceny na wartości liczbowe, które można przetwarzać i porównywać w całym zakresie problemu. Dla każdego elementu hierarchii ustalana jest waga liczbowa lub priorytet , co pozwala na porównanie różnych i często niewspółmiernych elementów w racjonalny i spójny sposób. Ta zdolność odróżnia AHP od innych technik podejmowania decyzji.

W końcowym etapie procesu dla każdej z alternatyw decyzyjnych obliczane są priorytety liczbowe. Liczby te reprezentują względną zdolność alternatyw do osiągnięcia celu decyzyjnego, więc pozwalają na bezpośrednie rozważenie różnych sposobów działania.

Kilka firm dostarcza oprogramowanie komputerowe pomagające w korzystaniu z tego procesu. [ wymagane wyjaśnienie ] Chociaż może być używany przez osoby pracujące nad prostymi decyzjami, Analityczny Proces Hierarchii (AHP) jest najbardziej przydatny tam, gdzie zespoły ludzi pracują nad złożonymi problemami, zwłaszcza tymi o wysokiej stawce, obejmującymi ludzkie postrzeganie i osądy, których rozwiązania mieć długofalowe skutki. Ma wyjątkowe zalety, gdy ważne elementy decyzji są trudne do oszacowania lub porównania, lub gdy komunikacja między członkami zespołu jest utrudniona z powodu ich różnych specjalizacji, terminologii lub perspektyw.

Sytuacje decyzyjne, do których można zastosować AHP, obejmują:

  • Wybór – wybór jednej alternatywy z danego zestawu alternatyw, zwykle tam, gdzie występuje wiele kryteriów decyzyjnych.
  • Ranking – uporządkowanie zestawu alternatyw od najbardziej do najmniej pożądanych.
  • Priorytetyzacja - określenie względnej zasługi członków zestawu alternatyw, w przeciwieństwie do wybierania jednej lub jedynie ich uszeregowania
  • Alokacja zasobów — przydział zasobów między zestaw alternatyw
  • Benchmarking – Porównanie procesów we własnej organizacji z procesami innych najlepszych organizacji
  • Zarządzanie jakością – Zajmowanie się wielowymiarowymi aspektami jakości i doskonalenia jakości
  • Rozwiązywanie konfliktów – rozstrzyganie sporów między stronami o pozornie niezgodnych celach lub stanowiskach

Zastosowania AHP w złożonych sytuacjach decyzyjnych liczono w tysiącach i przyniosły rozległe wyniki w problemach związanych z planowaniem , alokacją zasobów , ustalaniem priorytetów i wyborem spośród alternatyw. Inne obszary obejmowały prognozowanie , kompleksowe zarządzanie jakością , reorganizację procesów biznesowych , wdrażanie funkcji jakości i zrównoważoną kartę wyników . Wiele aplikacji AHP nigdy nie jest zgłaszanych całemu światu, ponieważ mają miejsce na wysokich szczeblach dużych organizacji, gdzie względy bezpieczeństwa i prywatności zabraniają ich ujawniania. Ale niektóre zastosowania AHP są omawiane w literaturze. Ostatnio były to m.in.

AHP jest czasami używany do projektowania bardzo specyficznych procedur dla określonych sytuacji, takich jak ocena budynków według znaczenia historycznego. Niedawno zastosowano go w projekcie, który wykorzystuje wideo do oceny stanu autostrad w Wirginii . Inżynierowie drogownictwa wykorzystali ją najpierw do określenia optymalnego zakresu projektu , a następnie do uzasadnienia jego budżetu przed ustawodawcami .

Wagi macierzy oceny AHP można skorygować o wagi obliczone metodą entropii. Ten wariant metody AHP nosi nazwę AHP-EM.

Edukacja i badania naukowe

Chociaż korzystanie z procesu hierarchii analitycznej nie wymaga specjalistycznego szkolenia akademickiego, jest uważane za ważny przedmiot w wielu instytucjach szkolnictwa wyższego, w tym w szkołach inżynierskich i wyższych szkołach biznesu . Jest to szczególnie ważny przedmiot w jakości i jest nauczany na wielu specjalistycznych kursach, w tym Six Sigma , Lean Six Sigma i QFD .

Wartość AHP jest uznawana w krajach rozwiniętych i rozwijających się na całym świecie. Przykładem są Chiny – blisko sto chińskich uniwersytetów oferuje zajęcia z AHP, a wielu doktorantów wybiera AHP jako przedmiot swoich badań i rozpraw. W Chinach opublikowano ponad 900 artykułów na ten temat i istnieje co najmniej jedno chińskie czasopismo naukowe poświęcone wyłącznie AHP.

Międzynarodowe Sympozjum na temat Procesu Hierarchii Analitycznej (ISAHP) organizuje co dwa lata spotkania naukowców i praktyków zainteresowanych tą dziedziną. Poruszany jest szeroki zakres tematów. Te z 2005 r. obejmowały „Ustanowienie standardów płatności dla chirurgów”, „Strategiczne planowanie rozwoju technologii” i „Odbudowę infrastruktury w zdewastowanych krajach”. Na spotkaniu w Valparaíso w Chile w 2007 roku przedstawiono ponad 90 referatów z 19 krajów, w tym z USA, Niemiec, Japonii, Chile, Malezji i Nepalu. Podobna liczba referatów została zaprezentowana na sympozjum w 2009 roku w Pittsburghu w Pensylwanii , na którym reprezentowanych było 28 krajów. Tematy referatów obejmowały stabilizację gospodarczą na Łotwie , wybór portfela w sektorze bankowym , zarządzanie pożarami lasów w celu złagodzenia globalnego ocieplenia oraz wiejskie mikroprojekty w Nepalu .

Używać

Typowe urządzenie do wprowadzania ocen w sesji decyzyjnej grupy AHP

Jak widać w poniższym materiale, użycie AHP wiąże się z matematyczną syntezą wielu sądów dotyczących danego problemu decyzyjnego. Nie jest niczym niezwykłym, że wyroki te liczą się w dziesiątkach, a nawet setkach. Chociaż obliczenia można wykonać ręcznie lub za pomocą kalkulatora, znacznie częściej stosuje się jedną z kilku komputerowych metod wprowadzania i syntezy osądów. Najprostsze z nich obejmują standardowe oprogramowanie arkusza kalkulacyjnego, podczas gdy najbardziej złożone wykorzystują oprogramowanie niestandardowe, często wzbogacone o specjalne urządzenia do pozyskiwania osądów decydentów zebranych w sali konferencyjnej.

Procedurę korzystania z AHP można podsumować następująco:

  1. Zamodeluj problem jako hierarchię zawierającą cel decyzyjny, alternatywy dla jego osiągnięcia oraz kryteria oceny alternatyw.
  2. Ustal priorytety wśród elementów hierarchii, dokonując serii ocen opartych na parach porównań elementów. Na przykład, porównując potencjalne zakupy nieruchomości komercyjnych, inwestorzy mogą powiedzieć, że wolą lokalizację od ceny i cenę od terminu.
  3. Zsyntetyzuj te osądy, aby uzyskać zestaw ogólnych priorytetów dla hierarchii. Łączyłoby to oceny inwestorów dotyczące lokalizacji, ceny i czasu dla nieruchomości A, B, C i D w ogólne priorytety dla każdej nieruchomości.
  4. Sprawdź spójność wyroków.
  5. Podejmij ostateczną decyzję na podstawie wyników tego procesu.

Kroki te są dokładniej opisane poniżej.

Modeluj problem jako hierarchię

Pierwszym krokiem w procesie hierarchii analitycznej jest modelowanie problemu jako hierarchii. W ten sposób uczestnicy badają aspekty problemu na poziomach od ogólnego do szczegółowego, a następnie wyrażają go w wielopoziomowy sposób wymagany przez AHP. Pracując nad zbudowaniem hierarchii, zwiększają swoje zrozumienie problemu, jego kontekstu oraz wzajemnych myśli i uczuć dotyczących obu.

Zdefiniowane hierarchie

Hierarchia to warstwowy system uszeregowania i organizowania ludzi, rzeczy, idei itp., w którym każdy element systemu, z wyjątkiem najwyższego, jest podporządkowany jednemu lub kilku innym elementom. Chociaż pojęcie hierarchii jest łatwe do zrozumienia intuicyjnie, można je również opisać matematycznie. Diagramy hierarchii często mają kształt piramidy, ale poza pojedynczym elementem na szczycie hierarchia nie ma koniecznie kształtu piramidy.

Organizacje ludzkie mają często strukturę hierarchiczną, w której system hierarchiczny służy do przydzielania obowiązków, sprawowania przywództwa i ułatwiania komunikacji. Znane hierarchie „rzeczy” obejmują jednostkę wieżową komputera stacjonarnego na „górze”, z podrzędnym monitorem, klawiaturą i myszą „poniżej”.

W świecie idei używamy hierarchii, aby uzyskać szczegółową wiedzę o złożonej rzeczywistości: porządkujemy rzeczywistość w jej części składowe, a te z kolei we własne części składowe, schodząc w dół hierarchii na tyle poziomów, na ile nam zależy. Na każdym kroku skupiamy się na zrozumieniu pojedynczego elementu całości, chwilowo ignorując inne elementy na tym i wszystkich innych poziomach. Przechodząc przez ten proces, zwiększamy nasze globalne zrozumienie dowolnej złożonej rzeczywistości, którą badamy.

Pomyśl o hierarchii stosowanej przez studentów medycyny podczas nauki anatomii — osobno rozważają układ mięśniowo-szkieletowy (w tym części i podczęści, takie jak ręka oraz mięśnie i kości składowe), układ krążenia (i jego wiele poziomów i gałęzi), układ nerwowy ( oraz jego liczne komponenty i podsystemy) itd., dopóki nie obejmą wszystkich systemów i ważnych podpodziałów każdego z nich. Zaawansowani studenci kontynuują podział aż do poziomu komórki lub cząsteczki. W końcu uczniowie rozumieją „ogólny obraz” i znaczną liczbę jego szczegółów. Nie tylko to, ale rozumieją stosunek poszczególnych części do całości. Pracując hierarchicznie, zdobyli wszechstronne zrozumienie anatomii.

Podobnie, gdy podchodzimy do złożonego problemu decyzyjnego, możemy użyć hierarchii, aby zintegrować duże ilości informacji z naszym zrozumieniem sytuacji. Budując tę ​​strukturę informacji, tworzymy coraz lepszy obraz problemu jako całości.

Hierarchie w AHP

Hierarchia AHP to uporządkowany sposób modelowania podejmowanych decyzji. Składa się z ogólnego celu, grupy opcji lub alternatyw dla osiągnięcia celu oraz grupy czynników lub kryteriów, które wiążą alternatywy z celem. Kryteria można dalej podzielić na podkryteria, podkryteria i tak dalej, na tylu poziomach, ile wymaga problem. Kryterium może nie być stosowane jednolicie, ale może mieć stopniowane różnice, takie jak odrobina słodyczy jest przyjemna, ale nadmiar słodyczy może być szkodliwy. W takim przypadku kryterium dzieli się na podkryteria wskazujące różne intensywności kryterium, takie jak: mała, średnia, wysoka i te intensywności są priorytetyzowane poprzez porównania w ramach kryterium macierzystego, słodyczy. Publikowane opisy aplikacji AHP często zawierają diagramy i opisy ich hierarchii; w tym artykule pokazano kilka prostych. Bardziej złożone hierarchie AHP zostały zebrane i przedrukowane w co najmniej jednej książce. Bardziej złożone hierarchie można znaleźć na specjalnej stronie dyskusji dla tego artykułu .

Projekt dowolnej hierarchii AHP będzie zależał nie tylko od natury danego problemu, ale także od wiedzy, osądów, wartości, opinii, potrzeb, pragnień itp. Uczestników procesu decyzyjnego. Konstruowanie hierarchii zwykle wiąże się z poważną dyskusją, badaniami i odkryciami zaangażowanych osób. Nawet po początkowej konstrukcji można go zmienić, aby dostosować się do nowo wymyślonych kryteriów lub kryteriów, które pierwotnie nie były uważane za ważne; alternatywy można również dodawać, usuwać lub zmieniać.

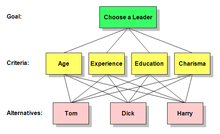
Aby lepiej zrozumieć hierarchie AHP, rozważ problem decyzyjny z celem do osiągnięcia, trzema alternatywnymi sposobami osiągnięcia celu i czterema kryteriami, względem których należy mierzyć alternatywy.

Taka hierarchia może być zwizualizowana jako diagram, taki jak ten bezpośrednio poniżej, z celem na górze, trzema alternatywami na dole i czterema kryteriami pomiędzy nimi. Istnieją przydatne terminy opisujące części takich diagramów: Każde pudełko nazywane jest węzłem. Węzeł, który jest połączony z jednym lub kilkoma węzłami na niższym poziomie, nazywany jest węzłem nadrzędnym. Węzły, z którymi jest tak połączony, nazywane są jego dziećmi.

Stosując te definicje do poniższego diagramu, cel jest rodzicem czterech kryteriów, a cztery kryteria są dziećmi celu. Każde kryterium jest rodzicem trzech Alternatyw. Zauważ, że są tylko trzy Alternatywy, ale na diagramie każda z nich jest powtórzona pod każdym rodzicem.

Prosta hierarchia AHP. Istnieją trzy Alternatywy dla osiągnięcia Celu i cztery Kryteria, którymi należy się kierować przy podejmowaniu decyzji.

Aby zmniejszyć rozmiar wymaganego rysunku, często przedstawia się hierarchie AHP, jak pokazano na poniższym diagramie, z tylko jednym węzłem dla każdej alternatywy i wieloma liniami łączącymi alternatywy i kryteria, które mają do nich zastosowanie. Aby uniknąć bałaganu, linie te są czasami pomijane lub zmniejszane. Niezależnie od tego typu uproszczeń na diagramie, w rzeczywistej hierarchii każde kryterium jest indywidualnie powiązane z alternatywami. Linie można uważać za skierowane w dół od rodzica na jednym poziomie do jego dzieci na niższym poziomie.

Hierarchia AHP do wyboru lidera. Jest jeden cel, trzech kandydatów i cztery kryteria wyboru spośród nich.

Oceń hierarchię

Po zbudowaniu hierarchii uczestnicy analizują ją poprzez serię porównań parami, które wyprowadzają numeryczne skale pomiaru dla węzłów. Kryteria są porównywane parami z celem pod względem ważności. Alternatywy są porównywane parami z każdym z kryteriów preferencji. Porównania są przetwarzane matematycznie, a dla każdego węzła ustalane są priorytety.

Rozważ powyższy przykład „Wybierz lidera”. Ważnym zadaniem decydentów jest określenie wagi, jaką należy nadać każdemu kryterium przy dokonywaniu wyboru lidera. Kolejnym ważnym zadaniem jest określenie wagi, jaką należy przypisać każdemu kandydatowi w odniesieniu do każdego z kryteriów. AHP nie tylko pozwala im to zrobić, ale pozwala im nadać znaczącą i obiektywną wartość liczbową każdemu z czterech kryteriów.

W przeciwieństwie do większości ankiet, które przyjmują pięciostopniową skalę Likerta , kwestionariusz AHP ma od 9 do 1 do 9.

Ustal priorytety

W tej sekcji wyjaśniono priorytety, pokazano, w jaki sposób są one ustalane, i podano prosty przykład.

Priorytety zdefiniowane i wyjaśnione

Priorytety to liczby powiązane z węzłami hierarchii AHP. Reprezentują względne wagi węzłów w dowolnej grupie.

Podobnie jak prawdopodobieństwa, priorytety to liczby bezwzględne z przedziału od zera do jednego, bez jednostek i wymiarów. Węzeł o priorytecie 0,200 ma dwukrotnie większą wagę w osiągnięciu celu niż węzeł o priorytecie 0,100, dziesięciokrotnie większą niż węzeł o priorytecie 0,020 i tak dalej. W zależności od danego problemu „waga” może odnosić się do ważności, preferencji, prawdopodobieństwa lub dowolnego czynnika branego pod uwagę przez decydentów.

Priorytety są rozłożone w hierarchii zgodnie z jej architekturą, a ich wartości zależą od informacji wprowadzanych przez użytkowników procesu. Priorytety Celu, Kryteria i Alternatywy są ściśle ze sobą powiązane, ale należy je rozpatrywać oddzielnie.

Z definicji priorytet Celu to 1.000. Priorytety alternatyw zawsze sumują się do 1.000. Sprawy mogą się skomplikować z wieloma poziomami Kryteriów, ale jeśli jest tylko jeden poziom, ich priorytety również sumują się do 1.000. Wszystko to ilustrują priorytety w poniższym przykładzie.

Prosta hierarchia AHP z powiązanymi domyślnymi priorytetami

Zauważ, że priorytety na każdym poziomie przykładu — cel, kryteria i alternatywy — sumują się do 1000.

Pokazane priorytety to te, które istnieją przed wprowadzeniem jakichkolwiek informacji o wagach kryteriów lub alternatyw, więc wszystkie priorytety na każdym poziomie są równe. Nazywa się je domyślnymi priorytetami hierarchii. Jeśli do tej hierarchii dodano piąte kryterium, domyślny priorytet każdego kryterium wynosiłby 0,200. Gdyby istniały tylko dwie Alternatywy, każda z nich miałaby domyślny priorytet 0,500.

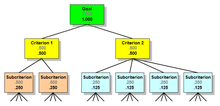
Dwie dodatkowe koncepcje mają zastosowanie, gdy hierarchia ma więcej niż jeden poziom kryteriów: priorytety lokalne i priorytety globalne. Rozważ hierarchię pokazaną poniżej, która zawiera kilka Kryteriów Podrzędnych w ramach każdego Kryterium.

Bardziej złożona hierarchia AHP z lokalnymi i globalnymi domyślnymi priorytetami. Ze względu na przejrzystość, na schemacie nie pojawiają się warianty decyzyjne.

Priorytety lokalne, pokazane na szaro, reprezentują względne wagi węzłów w grupie rodzeństwa w stosunku do ich rodzica. Lokalne priorytety każdej grupy Kryteriów i ich siostrzanych Kryteriów Podrzędnych sumują się do 1000. Priorytety globalne, pokazane na czarno, uzyskuje się przez pomnożenie lokalnych priorytetów rodzeństwa przez globalny priorytet ich rodziców. Globalne priorytety dla wszystkich kryteriów podrzędnych na poziomie sumują się do 1.000.

Zasada jest następująca: w hierarchii globalne priorytety węzłów potomnych zawsze sumują się z globalnym priorytetem ich rodzica. W grupie dzieci lokalne priorytety sumują się do 1.000.

Do tej pory przyglądaliśmy się tylko domyślnym priorytetom. W miarę postępu procesu hierarchii analitycznej priorytety będą zmieniać się z wartości domyślnych, gdy decydenci wprowadzają informacje o znaczeniu różnych węzłów. Robią to, dokonując serii porównań parami.

Praktyczne przykłady

Doświadczeni praktycy wiedzą, że najlepszym sposobem zrozumienia AHP jest analiza przypadków i przykładów. W załączniku do tego artykułu przedstawiono dwa szczegółowe studia przypadku , opracowane specjalnie jako szczegółowe przykłady nauczania:

Niektóre książki na temat AHP zawierają praktyczne przykłady jego użycia, chociaż zazwyczaj nie mają one być pomocami w nauce krok po kroku. Jeden z nich zawiera garść rozbudowanych przykładów oraz około 400 hierarchii AHP, krótko opisanych i zilustrowanych rysunkami. Wiele przykładów zostało omówionych, głównie dla profesjonalistów, w artykułach opublikowanych przez International Symposium on the Analytic Hierarchy Process .

Krytyka

AHP jest zawarte w większości podręczników do badań operacyjnych i nauk o zarządzaniu i jest nauczane na wielu uniwersytetach; jest szeroko stosowany w organizacjach, które dokładnie zbadały jego teoretyczne podstawy. Chociaż panuje powszechna zgoda co do tego, że jest ona zarówno technicznie ważna, jak i praktyczna, metoda ta ma swoich krytyków. Na początku lat 90. seria debat między krytykami i zwolennikami AHP została opublikowana w Management Science i The Journal of the Operational Research Society, dwóch prestiżowych czasopismach, na które Saaty i jego współpracownicy mieli znaczący wpływ. Wydaje się, że debaty te zostały rozstrzygnięte na korzyść AHP:

  • Dogłębny artykuł omawiający i obalający akademicką krytykę AHP został opublikowany w Operations Research w 2001 roku.
  • Management Science z 2008 roku , w którym dokonano przeglądu 15 lat postępu we wszystkich obszarach podejmowania decyzji wielokryterialnych, wykazał, że liczba publikacji AHP znacznie przewyższa publikacje w jakimkolwiek innym obszarze, określając ich wzrost jako „ogromny”.
  • Również w 2008 roku główne stowarzyszenie badań operacyjnych, Instytut Badań Operacyjnych i Nauk o Zarządzaniu, formalnie uznało szeroki wpływ AHP na swoje dziedziny.

Nadal pojawiają się sporadyczne głosy krytyczne. W artykule z 1997 roku zbadano możliwe błędy w skali werbalnej (w porównaniu z numeryczną) często używanej w porównaniach parami AHP. Inny z tego samego roku twierdził, że nieszkodliwe zmiany w modelu AHP mogą wprowadzić porządek tam, gdzie go nie ma. Artykuł z 2006 roku wykazał, że dodanie kryteriów, dla których wszystkie alternatywy działają jednakowo, może zmienić priorytety alternatyw.

W 2021 roku pierwsza kompleksowa ocena AHP została opublikowana w książce autorstwa dwóch naukowców z Uniwersytetu Technicznego w Walencji i Universidad Politécnica de Cartagena , opublikowanej przez Springer Nature . Na podstawie badania empirycznego i obiektywnych zeznań 101 badaczy badanie wykazało co najmniej 30 wad w AHP i okazało się, że nie nadaje się do złożonych problemów, aw niektórych sytuacjach nawet do małych problemów.

Odwrócenie rangi

Podejmowanie decyzji obejmuje uszeregowanie alternatyw pod względem kryteriów lub atrybutów tych alternatyw. Aksjomatem niektórych teorii decyzyjnych jest to, że kiedy do problemu decyzyjnego dodawane są nowe alternatywy, ranking starych alternatyw nie może się zmieniać – „ odwrócenie rang ” nie może nastąpić.

Istnieją dwie szkoły myślenia o odwróceniu rang. Utrzymuje się, że nowe alternatywy, które nie wprowadzają żadnych dodatkowych atrybutów, w żadnym wypadku nie powinny powodować odwrócenia rangi. Drugi utrzymuje, że istnieją pewne sytuacje, w których można rozsądnie oczekiwać odwrócenia rang. Oryginalna formuła AHP pozwalała na odwrócenie rang. W 1993 roku Forman wprowadził drugi tryb syntezy AHP, zwany trybem syntezy idealnej, w celu rozwiązania sytuacji wyboru, w których dodanie lub usunięcie „nieistotnej” alternatywy nie powinno i nie spowoduje zmiany w szeregach istniejących alternatyw. Obecna wersja AHP może pomieścić obie te szkoły - jej idealny tryb zachowuje rangę, podczas gdy tryb dystrybucyjny pozwala na zmianę rang. Każdy z trybów jest wybierany w zależności od problemu.

Odwrócenie rangi i AHP są obszernie omówione w artykule z 2001 roku w Operations Research , a także w rozdziale zatytułowanym Zachowanie i odwrócenie rangi w aktualnej podstawowej książce o AHP. Ten ostatni przedstawia opublikowane przykłady odwrócenia rang z powodu dodania kopii i prawie kopii alternatywy, z powodu nieprzechodniości reguł decyzyjnych, z powodu dodania alternatyw fantomowych i wabików oraz ze względu na zjawisko przełączania w funkcjach użyteczności. Omówiono również tryby dystrybucyjne i idealne AHP.

W 2014 roku odkryto nową formę odwrócenia rang AHP, w której AHP powoduje odwrócenie kolejności rang podczas eliminowania nieistotnych danych, czyli danych, które nie różnicują alternatyw.

Istnieją różne rodzaje odwrócenia rang. Również inne metody oprócz AHP mogą wykazywać takie odwrócenie rang. Więcej dyskusji na temat odwracania rang za pomocą AHP i innych metod MCDM znajduje się na odwracania rang na stronie podejmowania decyzji .

Niemonotoniczność niektórych metod ekstrakcji wagowej

W macierzy porównań można zastąpić orzeczenie mniej korzystnym orzeczeniem, a następnie sprawdzić, czy wskazanie nowego pierwszeństwa nie stanie się mniej korzystne niż pierwszeństwo pierwotne. W kontekście macierzy turniejowych Oskar Perron udowodnił, że metoda głównego prawego wektora własnego nie jest monotoniczna. To zachowanie można również wykazać dla odwrotnych macierzy nxn, gdzie n > 3. Alternatywne podejścia są omówione gdzie indziej.

Zobacz też

Dalsza lektura

  •     Saaty, Thomas L. Podejmowanie decyzji dla przywódców: analityczny proces hierarchii decyzji w złożonym świecie (1982). Belmont, Kalifornia: Wadsworth. ISBN 0-534-97959-9 ; Książka w miękkiej okładce, Pittsburgh: RWS. ISBN 0-9620317-0-4 . „Koncentruje się na praktycznym zastosowaniu AHP; krótko omawia teorię”.
  •   Saaty, Thomas L. Podstawy podejmowania decyzji i teoria priorytetów z analitycznym procesem hierarchii (1994). Pittsburgh: RWS. ISBN 0-9620317-6-3 . „Dokładne przedstawienie teoretycznych aspektów AHP”.
  •   Saaty, Thomas L. Matematyczne zasady podejmowania decyzji (Principia Mathematica Decernendi) (2009). Pittsburgh: RWS. ISBN 1-888603-10-0 . „Kompleksowe omówienie AHP, jego następcy ANP i dalszy rozwój ich podstawowych koncepcji”.
  •   Saaty, Thomas L., z Ernestem H. Formanem. Hierarchon: słownik hierarchii . (1992) Pittsburgh: RWS. ISBN 0-9620317-5-5 . „Dziesiątki ilustracji i przykładów hierarchii AHP. Początkowa klasyfikacja pomysłów związanych z planowaniem, rozwiązywaniem konfliktów i podejmowaniem decyzji”.
  •       Saaty, Thomas L., z Luisem G. Vargasem Logika priorytetów: zastosowania w biznesie, energetyce, zdrowiu i transporcie (1982). Boston: Kluwer-Nijhoff. ISBN 0-89838-071-5 (oprawa twarda) ISBN 0-89838-078-2 (oprawa miękka). Opublikowane ponownie w 1991 przez RWS, ISBN 1-888603-07-0 .
  • Kardi Teknomo. Samouczek procesu hierarchii analitycznej (2012). Revoledu.
  •     Kearns, Kevin P.; Saaty, Thomas L. Planowanie analityczne: organizacja systemów (1985). Oksford: Pergamon Press. ISBN 0-08-032599-8 . Opublikowane ponownie w 1991 przez RWS, ISBN 1-888603-07-0 .
  •   z Joycem Alexandrem. Rozwiązywanie konfliktów: proces hierarchii analitycznej (1989). Nowy Jork: Praeger. ISBN 0-275-93229-X
  •   Vargas, Luis L.; Saaty, Thomas L. Przewidywanie, projekcja i prognozowanie: zastosowania procesu hierarchii analitycznej w ekonomii, finansach, polityce, grach i sporcie (1991). Boston: Kluwer akademicki. ISBN 0-7923-9104-7
  •   Vargas, Luis L.; Saaty, Thomas L. Podejmowanie decyzji w środowiskach ekonomicznych, społecznych i technologicznych (1994). Pittsburgh: RWS. ISBN 0-9620317-7-1
  •   Vargas, Luis L.; Saaty, Thomas L. Modele, metody, koncepcje i zastosowania analitycznego procesu hierarchii (2001). Boston: Kluwer akademicki. ISBN 0-7923-7267-0
  •   Peniwati, Kirti; Vargas, Luis L. Grupa Podejmowanie decyzji: wyciąganie i godzenie różnic (2007). Pittsburgh: RWS. ISBN 1-888603-08-9

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Analytic_hierarchy_process&oldid=1131805792 ”