Reakcja na kolizję

W kontekście symulacji mechaniki klasycznej i silników fizyki stosowanych w grach wideo reakcja na kolizję dotyczy modeli i algorytmów do symulacji zmian ruchu dwóch ciał stałych po zderzeniu i innych formach kontaktu .

Sztywny kontakt ciała

Fazy ​​ściskania i rozszerzania zderzenia dwóch ciał stałych

Dwa ciała sztywne w ruchu swobodnym, potencjalnie pod działaniem sił, można modelować, rozwiązując ich równania ruchu za pomocą technik całkowania numerycznego . W przypadku zderzenia właściwości kinetyczne dwóch takich ciał wydają się ulegać natychmiastowej zmianie, co zwykle powoduje odbijanie się ciał od siebie, przesuwanie się lub osiadanie we względnym kontakcie statycznym, w zależności od elastyczności materiałów i konfiguracji zderzenia .

Siły kontaktu

Źródeł zjawiska lub reakcji odbicia można doszukiwać się w zachowaniu rzeczywistych ciał, które w przeciwieństwie do swoich idealnie sztywnych wyidealizowanych odpowiedników podlegają niewielkiemu ściskaniu podczas zderzenia, a następnie rozszerzaniu się przed oddzieleniem. Faza kompresji przekształca energię kinetyczną ciał w energię potencjalną i do pewnego stopnia ciepło. Faza ekspansji przekształca energię potencjalną z powrotem w energię kinetyczną.

Podczas faz ściskania i rozszerzania dwóch zderzających się ciał, każde ciało wytwarza siły reakcji na drugim w punktach styku, tak że suma sił reakcji jednego ciała jest równa co do wartości, ale skierowana przeciwnie do sił drugiego, jak zgodnie z newtonowską zasadą akcji i reakcji. Jeśli pominie się skutki tarcia, zderzenie jest postrzegane jako mające wpływ tylko na składową prędkości skierowaną wzdłuż normalnej kontaktu i pozostawiające nienaruszone składowe styczne

Reakcja

Stopień względnej energii kinetycznej zachowanej po zderzeniu, zwany restytucją , zależy od sprężystości materiałów ciał. Współczynnik restytucji między dwoma danymi materiałami jest modelowany jako stosunek ${\ Displaystyle e \ in [0..1]}$ prędkości po zderzeniu punktu styku wzdłuż normalnej kontaktu mi , w odniesieniu do względnej prędkości przed zderzeniem tego samego punktu wzdłuż tej samej normalnej. Współczynniki te są zwykle określane empirycznie dla różnych par materiałów, takich jak drewno na betonie lub guma na drewnie. Wartości $zbliżone do$ wskazują zderzenia nieelastyczne , takie jak uderzenie kawałka miękkiej gliny o podłogę, podczas gdy wartości bliskie jedności reprezentują zderzenia wysoce elastyczne, takie jak odbijanie się gumowej piłki od ściany. Strata energii kinetycznej odnosi się do jednego ciała względem drugiego. Zatem całkowity pęd obu ciał względem pewnego wspólnego odniesienia pozostaje niezmieniony po zderzeniu, zgodnie z zasadą zachowania pędu .

Tarcie

Tarcie spowodowane niedoskonałościami mikrostruktury powierzchni

Innym ważnym zjawiskiem kontaktowym jest tarcie powierzchniowe, siła, która utrudnia względny ruch dwóch stykających się powierzchni lub ruch ciała w płynie. W tym podrozdziale omówimy tarcie powierzchniowe dwóch ciał we względnym kontakcie statycznym lub ślizgowym. W świecie rzeczywistym tarcie wynika z niedoskonałej mikrostruktury powierzchni, których występy zazębiają się ze sobą, generując siły reakcji styczne do powierzchni.

Aby pokonać tarcie między dwoma ciałami w kontakcie statycznym, powierzchnie muszą w jakiś sposób odsunąć się od siebie. W ruchu stopień powinowactwa powierzchniowego jest zmniejszony, a zatem ciała w ruchu ślizgowym mają tendencję do stawiania mniejszego oporu ruchu. Te dwie kategorie tarcia nazywane są odpowiednio tarciem statycznym i tarciem dynamicznym .

Zastosowana siła

Jest to siła, która jest przykładana do przedmiotu przez inny przedmiot lub osobę. Kierunek przyłożonej siły zależy od sposobu przyłożenia siły.

Normalna siła

Jest to siła podparcia wywierana na obiekt, który styka się z innym stabilnym przedmiotem. Siła normalna jest czasami nazywana siłą nacisku, ponieważ jej działanie dociska powierzchnię do siebie. Siła normalna jest zawsze skierowana w stronę obiektu i działa prostopadle do przyłożonej siły.

Siła tarcia

Jest to siła wywierana przez powierzchnię, gdy obiekt porusza się po niej lub próbuje się po niej poruszać. Siła tarcia przeciwdziała ruchowi obiektu. Tarcie powstaje, gdy dwie powierzchnie są ściśle dociśnięte do siebie, powodując przyciąganie sił międzycząsteczkowych między cząsteczkami dwóch różnych powierzchni. Jako takie, tarcie zależy od natury dwóch powierzchni i stopnia, w jakim są one dociskane do siebie. Tarcie zawsze działa równolegle do stykającej się powierzchni i przeciwnie do kierunku ruchu. Siłę tarcia można obliczyć za pomocą równania.

Impulsowy model kontaktu

siła ${\ Displaystyle \ mathbf {f} (t) \ in \ mathbb {R} ^ {3}}$ , zależna od czasu ${\ Displaystyle t \ in \ mathbb {R} }$ , działając na ciało o założonej ${\ Displaystyle \ lbrack t_ {0}.. t_ {1} \ rbrack}$$przedział$ czasu generuje zmianę pędu ciała ${\ Displaystyle \ mathbf {p} (t) = m \ mathbf {v} (t)}$$z tego$ wynikającą zmianą prędkości Zmiana pędu, nazywana impulsem i oznaczana przez ${\ Displaystyle \ mathbf {j} \ in \ mathbb {R} ^ {3}}$ jest zatem obliczana jako

${\ Displaystyle \ mathbf {j} = \ int _ {t_ {0}} ^ {t_ {1}} \ mathbf {f} dt}$

Dla stałego impulsu $równanie$ , że ${\ Displaystyle t_ {1} \ rightarrow t_ {0} \ Rightarrow \ lewo | \ mathbf {f} \ prawo | \ rightarrow \ infty } , czyli$ mniejszy przedział czasu musi zostać skompensowany przez silniejszą siłę reakcji osiągnąć ten sam impuls. Podczas modelowania kolizji między wyidealizowanymi ciałami sztywnymi niepraktyczne jest symulowanie faz ściskania i rozszerzania geometrii ciała w przedziale czasu kolizji. Jednakże, zakładając, że można znaleźć siłę $mathbf {f}}$ która jest równa wszędzie z wyjątkiem punktu i taka $,$ że ​​​​granica ${\ displaystyle \$

${\ Displaystyle \ lim _ {t_ {1} \ rightarrow t_ {0}} \ int _ {t_ {0}} ^ {t_ {1}} \ mathbf {f } dt}$

$, aby symulować chwilową zmianę prędkości po zderzeniu.$ i jest równa , można wprowadzić pojęcie impulsów chwilowych

Model reakcji oparty na impulsie

Zastosowanie impulsów w miejscu zderzenia

Skutek siły reakcji ${\ Displaystyle \ mathbf {f} _ {r} (t) \ in \ mathbb {R} ^ {3}}$ w przedziale zderzenia ${\ Displaystyle [t_ {0}.. t_ {1}]}$ może zatem być reprezentowany przez natychmiastowy impuls reakcji ${\ Displaystyle \ mathbf {j} _ {r} (t )\in \mathbb {R} ^{3}}$ , obliczone jako

${\ Displaystyle \ mathbf {j} _ {r} = \ int _ {t_ {0}} ^ {t_ {1}} \ mathbf {f} _ {r} dt }$

Dedukując z zasady akcji i reakcji, jeśli impuls zderzenia przyłożony przez pierwsze ciało do drugiego ciała w punkcie styku ${\ Displaystyle \ mathbf {p} _ {r} \ in \ mathbb {R } ^ {3}}$ to ${\ Displaystyle \ mathbf {j} _ {r}}$ przeciwny impuls zastosowany przez drugie ciało na pierwszym to ${\ displaystyle - \ mathbf {j} _ {r }}$ . Rozkład ${\ Displaystyle \ pm \ mathbf {j} _ {r} = \ pm j_ {r} \ mathbf {\ kapelusz {n}}}$ na wielkość impulsu ${\ Displaystyle j_ {r} \ in \ mathbb {R}}$ i kierunek wzdłuż normalnej kontaktu ${\ Displaystyle \ mathbf {\ kapelusz {n}}}$ i jego zaprzeczenie ${\ Displaystyle - \ mathbf {\ hat {n}} }$ pozwala na wyprowadzenie wzoru na obliczenie zmiany prędkości liniowej i kątowej ciał w wyniku impulsów zderzenia. W kolejnych wzorach $,$ że punkt styku jest skierowany od ciała 1 do ciała

, że dana jest wielkość impulsu zderzenia i stosując prawa ruchu Newtona, zależność między prędkościami przed- i postliniowymi ciał jest następująca: ${\ displaystyle j_ {r}}$

	${\ Displaystyle \ mathbf {v '} _ {1} = \ mathbf {v} _ {1} - {\ Frac {j_ {r}} {m_ {1} }}}\mathbf {\kapelusz {n}}}$	(1a)
	${\ Displaystyle \ mathbf {v '} _ {2} = \ mathbf {v} _ {2} + {\ Frac {j_ {r}} {m_ {2} }}}\mathbf {\kapelusz {n}}}$	(1b)

gdzie dla ciała $,$$_$$_$ _

Podobnie dla prędkości kątowych

	${\ Displaystyle \ mathbf {\ omega '} _ {1} = \ mathbf {\ omega} _ {1} -j_ {r} \mathbf {I} _{1}^{-1}(\mathbf {r} _{1}\times \mathbf {\kapelusz {n}} )}$	(2a)
	${\ Displaystyle \ mathbf {\ omega '} _ {2} = \ mathbf {\ omega} _ {2} + j_ {r} \mathbf {I} _{2}^{-1}(\mathbf {r} _{2}\times \mathbf {\kapelusz {n}} )}$	(2b)

gdzie dla ciała th jest kątowa prędkość przed zderzeniem, $Displaystyle$ ja ${\ omega} _ {i} \ in \ mathbb {R} ^ {3}$${\ Displaystyle {\ omega '} _ {i} \ in \ mathbb {R} ^ {3}}$ to prędkość kątowa po zderzeniu, ${\ Displaystyle \ mathbf { ja} _ {i} \ in \ mathbb {R} ^ {3 \ razy 3}} jest tensorem$ bezwładności w światowym układzie odniesienia i ${R} ^ {3}}$${\ Displaystyle \ mathbf {r} _ {i} \ in \$$mathbb$ jest przesunięciem wspólnego punktu kontaktowego środka masy.

Prędkości ciał w punkcie kontaktu można obliczyć ${\ Displaystyle v_ {p1}, v_ {p2} \ in \ mathbb {R} ^ {3}}$ odpowiednie prędkości liniowe i kątowe, używając

${\ Displaystyle \ mathbf {v} _ {pi} = \ mathbf {v} _ {i} + \ mathbf {\ omega} _ {i} \ razy \ mathbf { r} _{i}}$

(3)

dla ${\ Displaystyle i = 1,2}$ . Współczynnik restytucji ${$ prędkości względnej przed zderzeniem $v} _ {r} = \ mathbf {v} _ {p2} - \mathbf {v} _ {p1}}$ punktu styku z względną prędkością po zderzeniu ${\ Displaystyle \ mathbf {v'} _ {r} = \ mathbf {v '} _ {p2} - \ mathbf {v'} _ {p1}}$ wzdłuż normalnej kontaktu ${\ Displaystyle \ mathbf {\ hat {n}}}$ w następujący sposób

${\ Displaystyle \ mathbf {v '} _ {r} \ cdot \ mathbf {\ kapelusz {n}} = -e \ mathbf {v} _ {r} \cdot \mathbf {\kapelusz {n}}}$

(4)

Podstawiając równania (1a), (1b), (2a), (2b) i (3) do równania (4) i rozwiązując wielkość impulsu reakcji, otrzymujemy jot $displaystyle j_ {r}}$ {

${\ Displaystyle j_ {r} = {\ Frac {- (1 + e) ​​\ mathbf {v} _ {r} \ cdot \ mathbf {\ kapelusz {n}}} {{m_ {1}}^{-1}+{m_{2}}^{-1}+({\mathbf {I} _{1}}^{-1}(\mathbf {r} _{1}\ razy \mathbf {\hat {n}} )\razy \mathbf {r} _{1}+{\mathbf {I} _{2}}^{-1}(\mathbf {r} _{2}\ razy \mathbf {\kapelusz {n}} )\razy \mathbf {r} _{2})\cdot \mathbf {\kapelusz {n}}}}}$

(5)

Obliczanie reakcji impulsowej

Zatem procedura obliczania prędkości liniowych po zderzeniu ${\ Displaystyle \ mathbf {\ omega '}$ prędkości kątowych $}$ następująco:

1. Obliczyć wielkość impulsu reakcji w kategoriach $,$${\ Displaystyle \ mathbf {v} _ {r}}$ m $\ Displaystyle m_ {1}}$ m $m_ {2}}$$\$ , ${\ Displaystyle \ mathbf {I} _ {1}}$ , ${\ Displaystyle \ mathbf {I} _ {2}}$ , ${\ Displaystyle \ mathbf {r} _ { 1}}$ , ${\ Displaystyle \ mathbf {r} _ {2}}$ , ${\ Displaystyle \ mathbf {\ kapelusz {n}}}$ i ${\ Displaystyle e}$ za pomocą równania (5)
2. ${$ wektor impulsu reakcji pod względem jego wielkości i skontaktuj się z normalnym $n }} }$$mathbf {\ hat$ używając ${\ Displaystyle \ mathbf {j} _ {r} = j_ {r} \ mathbf {\ kapelusz {n}}}$ .
3. Oblicz nowe prędkości liniowe ${\ Displaystyle \ mathbf {v '} _ {i}}$ w kategoriach starych prędkości ${\ Displaystyle \ mathbf {v} _ {i}}$ , masy ${\ Displaystyle m_ { i}}$ i wektor impulsu reakcji ${\ displaystyle \ mathbf {j} _ {r}}$ za pomocą równań (1a) i (1b)
4. Oblicz nowe prędkości kątowe w kategoriach starych prędkości kątowych, tensory bezwładności $ω$ ′ $Displaystyle \ mathbf {\ omega '}$$}$$\ Displaystyle \ mathbf {I} _ {i}}$ i impuls reakcji ${\ Displaystyle j_ {r}}$ za pomocą równań (2a) i (2b)

Impulsowy model tarcia

Model tarcia kulombowskiego - stożek tarcia

Jednym z najpopularniejszych modeli opisujących tarcie jest model tarcia Coulomba . Model ten $mathbb {R}} \ in \mathbb {R}}$ współczynniki $} _ {s} \ in \$ statycznego i dynamicznego takie, że ${\ Displaystyle {\ mu} _ {s}> {\ mu} _ {d}}$ . Współczynniki te opisują dwa rodzaje sił tarcia w kategoriach sił reakcji działających na ciała. $obliczane$ wielkości siły tarcia statycznego i jako ${\ Displaystyle f_ {r} =|\ mathbf {f} _ {r}|}$ w następujący sposób

	${\ displaystyle f_ {s} = {\ mu} _ {s} f_ {r}}$	(6a)
	${\ displaystyle f_ {d} = {\ mu} _ {d} f_ {r}}$	(6b)

Wartość określa maksymalną wielkość siły tarcia wymaganej do przeciwdziałania składowej stycznej dowolnej sumarycznej siły zewnętrznej przyłożonej do względnie statycznego ciała, tak aby pozostało $ono$ Tak więc, jeśli siła zewnętrzna jest wystarczająco duża, tarcie statyczne nie jest w stanie w pełni przeciwdziałać tej sile, w którym to momencie ciało nabiera prędkości i podlega tarciu dynamicznemu o wielkości działającemu przeciwko prędkości poślizgu fa re {\ displaystyle f_ { $}$ .

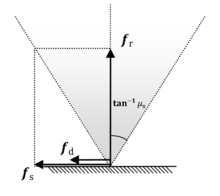
Model tarcia Coulomba skutecznie definiuje stożek tarcia, w którym składowa styczna siły wywieranej przez jedno ciało na powierzchnię drugiego w kontakcie statycznym jest przeciwdziałana przez równą i przeciwną siłę, tak że konfiguracja statyczna jest zachowana. I odwrotnie, jeśli siła wypadnie poza stożek, tarcie statyczne ustępuje tarciu dynamicznemu.

${r} \ w \ mathbb {R} ^ {3}}$$v$ kontakt \ $}$ punktu kontaktowego, wektor styczny ${\ Displaystyle \ mathbf {\ hat {t}} \ in \ mathbb {R} ^ {3 }}$ , prostopadły do ​​, można zdefiniować tak, że ${\ Displaystyle \ mathbf {\ hat {n}}}$

${\ Displaystyle \ mathbf {\ kapelusz {t}} = \ lewo \ {{\ rozpocząć {matryca} {\ frac {\mathbf {v} _{r}-(\mathbf {v} _{r}\cdot \mathbf {\kapelusz {n}})\mathbf {\kapelusz {n}}}}{|\mathbf {v} _{r}-(\mathbf {v} _{r}\cdot \mathbf {\hat {n}} )\mathbf {\hat {n}} |}}&\mathbf {v} _{r}\ cdot \mathbf {\kapelusz {n}} \neq 0&\\{\frac {\mathbf {f} _{e}-(\mathbf {f} _{e}\cdot \mathbf {\kapelusz {n}} )\mathbf {\hat {n}} }{|\mathbf {f} _{e}-(\mathbf {f} _{e}\cdot \mathbf {\hat {n}} )\mathbf {\hat {n}} |}}&\mathbf {v} _{r}\cdot \mathbf {\kapelusz {n}} =0&\mathbf {f} _{e}\cdot \mathbf {\kapelusz {n}} \neq 0\\\mathbf {0} &\mathbf {v} _{r}\cdot \mathbf {\kapelusz {n}} =0&\mathbf {f} _{e}\cdot \mathbf {\kapelusz { n}} =0\\\koniec{macierzy}}\prawo.}$

(7)

gdzie ${\ Displaystyle \ mathbf {f} _ {e} \ in \ mathbb {R} ^ {3}}$ jest sumą wszystkich sił zewnętrznych działających na ciało. Definicja wielu przypadków $∈$ wymagana do solidnego obliczenia rzeczywistej siły tarcia $\ Displaystyle \ mathbf {f} _ {f} \ in$ zarówno dla ogólnych, jak i szczegółowych stanów kontaktu. Nieformalnie, pierwszy przypadek oblicza wektor styczny wzdłuż składowej prędkości względnej prostopadłej do normalnej kontaktowej ${\ Displaystyle \ mathbf {\ hat {n}}}$ . Jeśli ta składowa wynosi zero, drugi przypadek wywodzi się $}$ kategoriach składowej stycznej siły zewnętrznej $_ { e}\w \mathbb {R} ^{3}}$ . Jeśli nie ma prędkości stycznej ani sił zewnętrznych, zakłada się, że nie ma tarcia i $wektor$ zerowy. Zatem ${\ Displaystyle \ mathbf {f} _ {f} \ in \ mathbb {R} ^ {3}}$ jest obliczane jako

${\ Displaystyle \ mathbf {f} _ {f} = \ left\{{\begin{matrix}-(\mathbf {f} _{e}\cdot \mathbf {\hat {t}} )\mathbf {\hat {t}} &\mathbf {v} _{r }\cdot \mathbf {\hat {t}} =0&\mathbf {f} _{e}\cdot \mathbf {\hat {t}} \leq f_{s}\\-f_{d}\mathbf { \hat {t}} &{\text{(inaczej)}}\\\end{matrix}}\right.}$

(8)

Równania (6a), (6b), (7) i (8) opisują model tarcia kulombowskiego w kategoriach sił. Dostosowując argument dla chwilowych impulsów, można wyprowadzić impulsową wersję modelu tarcia Coulomba, odnoszącą się do impulsu tarcia ${\ Displaystyle \ mathbf {j} _ {f} \ in \ mathbb {R} ^ {3}}$ , działając wzdłuż stycznej do impulsu reakcji $jot$$mathbb {R} ^{3}}$${\ Displaystyle \ mathbf {j} _ {r}$ . Całkowanie (6a) i (6b) po przedziale czasu kolizji ${\ Displaystyle [t_ {0}.. t_ {1}]}$ plony

	${\ Displaystyle j_ {s} = {\ mu} _ {s} j_ {r}}$	(9a)
	${\ Displaystyle j_ {d} = {\ mu} _ {d} j_ {r}}$	(9b)

gdzie ${\ Displaystyle j_ {r} =|\ mathbf {j} _ {r}|}$ to wielkość impulsu reakcji działającego wzdłuż normalnej kontaktu ${\ Displaystyle \ mathbf {\ hat {n}}}$ . Podobnie, zakładając stałą w całym przedziale czasu, całkowanie (8) daje ${\ displaystyle \ mathbf {\ hat {t}}}$

${\ Displaystyle \ mathbf {j} _ {f} =\left\{{\begin{matrix}-(m\mathbf {v} _{r}\cdot \mathbf {\hat {t}} )\mathbf {\hat {t}} &\mathbf {v} _{r}\cdot \mathbf {\kapelusz {t}} =0&m\mathbf {v} _{r}\cdot \mathbf {\kapelusz {t}} \leq j_{s}\\-j_{d} \mathbf {\hat {t}} &{\text{(inaczej)}}\\\end{macierz}}\right.}$

(10)

Równania (5) i (10) definiują impulsowy model kontaktu, który jest idealny do symulacji impulsowych. Korzystając z tego $} _ {d}},$ zachować ostrożność przy wyborze i ${\ Displaystyle {\ mu$ ponieważ wyższe wartości mogą wprowadzić dodatkową energię kinetyczną do systemu.

Zobacz też

• Wykrywanie kolizji

Notatki

• C. Vella, „Gravitas: rozszerzalna struktura silnika fizyki wykorzystująca zasady architektury oprogramowania zorientowanej obiektowo i opartej na wzorcach projektowych”, praca magisterska z technologii informatycznych, Uniwersytet Maltański, Msida, 2008.