Teoria Franka-Kamienieckiego

Podczas spalania teoria Franka-Kameneckiego wyjaśnia wybuch termiczny jednorodnej mieszaniny reagentów, znajdującej się w zamkniętym naczyniu o ścianach o stałej temperaturze . Jej nazwa pochodzi od rosyjskiego naukowca Davida A. Franka-Kameneckiego , który wraz z Nikołajem Semenowem opracował teorię w latach 30. XX wieku.

Opis problemu

$utrzymywane$ stałej temperaturze , zawierające jednorodną reagującą mieszaninę. Niech charakterystyczny rozmiar naczynia będzie ${\ displaystyle a}$ . Ponieważ mieszanina jest jednorodna, gęstość $stała$ . W początkowym okresie zapłonu zużycie stężenia reagentów jest znikome (patrz ${e}}$ { $t_$ ), więc wybuchem rządzi tylko równanie energii . Zakładając jednoetapową globalną reakcję ${\ Displaystyle {\ tekst {paliwo}} + {\ tekst {utleniacz}} \ rightarrow {\ tekst {produkty}} + q} ,$ gdzie ${\ displaystyle q}$ to ilość ciepła uwalnianego na jednostkę masy zużytego paliwa, a szybkość reakcji podlega prawu Arrheniusa , równanie energii przyjmuje postać

${\ Displaystyle \ rho c_ {v} {\ Frac {\ częściowe T} {\ częściowe t}} =\lambda \nabla ^{2}T+q\rho BY_{Fo}e^{-E/(RT)}}$

Gdzie

${\ displaystyle T}$	jest temperaturą mieszaniny;
${\ displaystyle c_ {v}}$	jest ciepłem właściwym przy stałej objętości;
${\ Displaystyle \ lambda}$	jest przewodnością cieplną ;
${\ Displaystyle B}$	jest czynnikiem przedwykładniczym o wymiarze jeden w czasie;
${\ Displaystyle Y_ {Fo}}$	jest początkowym ułamkiem masowym paliwa ;
$mi {\ Displaystyle E$	jest energią aktywacji ;
${\ displaystyle R}$	jest uniwersalną stałą gazową .

Brak wymiarowania

Bezwymiarowe skale czasu, temperatury, długości i wymiany ciepła można zdefiniować jako

${t} {t_ {e}}} ,\quad \theta ={\frac {\beta (T-T_{o})}{T_{o}}},\quad \eta ^{j}={\frac {r^{j}}{a }},\quad \delta ={\frac {t_{c}}{t_{e}}}}$

Gdzie

$\ Displaystyle t_ {c} = \ rho c_ {v} a ^ {2} / \ lambda}$	jest charakterystycznym czasem przewodzenia ciepła w naczyniu;
${\ Displaystyle t_ {f} = \ lewo (Bądź ^ {- \ beta} \ prawo) ^ {\! -1}}$	jest charakterystycznym czasem zużycia paliwa;
${\ Displaystyle t_ {e} = \ lewo (\ beta \ gamma Być ^ {- \ beta} \ prawej) ^ {\! -1}}$	jest charakterystycznym czasem wybuchu/zapłonu;
${\ displaystyle a}$	jest charakterystyczną odległością, np. promieniem naczynia;
${\ Displaystyle \ beta = E / (R \, T_ {o})}$	jest bezwymiarową energią aktywacji;
${\ Displaystyle \ gamma = (qY_ {Fo}) / (c_ {v} T_ {o})}$	jest parametrem wydzielania ciepła;
${\ Displaystyle \ delta}$	jest liczbą Damköhlera ;
${\ displaystyle r}$	jest współrzędną przestrzenną z początkiem w środku;
${\ Displaystyle j = 0}$	dla płyty płaskiej;
${\ Displaystyle j = 1}$	do naczynia cylindrycznego;
${\ Displaystyle j = 2}$	dla naczynia kulistego.

Uwaga

W typowym procesie spalania ${\ Displaystyle \ gamma \ około 6 {-} 8, \ \ beta \ około 30 {-} 100}$ tak, że ${\ styl wyświetlania \beta \gamma \gg 1}$ .

Dlatego ${\ Displaystyle t_ {f} = \ beta \ gamma t_ {e} \ gg 1}$ . Oznacza to, że czas zużycia paliwa jest znacznie dłuższy niż czas zapłonu, więc zużycie paliwa jest zasadniczo pomijalne w badaniu zapłonu.

Dlatego zakłada się, że stężenie paliwa pozostaje początkowym stężeniem paliwa ${\ displaystyle Y_ {Fo}}$ .

Podstawianie zmiennych bezwymiarowych w równaniu energetycznym ze wstępu

${\ Displaystyle {\ Frac {\ częściowe \ teta} {\ częściowe \ tau} }={\frac {1}{\delta }}{\frac {1}{\eta ^{j}}}{\frac {\partial }{\partial \eta }}\left(\eta ^{j }{\frac {\częściowe \theta}{\częściowe \eta}}\right)+e^{\theta /(1+\theta /\beta)}}$

Ponieważ człon wykładniczy można zlinearyzować $)}\około e^{\theta }}$$β$${\ Displaystyle e ^ {\ teta / (1 + \$ , stąd

${\ Displaystyle {\ Frac {\ częściowe \ teta} {\ częściowe \ tau}} = {\ Frac {1} {\delta}}{\frac {1}{\eta ^{j}}}{\frac {\częściowy}}{\częściowy \eta}}\left(\eta ^{j}{\frac {\częściowy \ theta }{\częściowa \eta }}\right)+e ^{\theta }}$

τ ${\ Displaystyle \ tau = 0}$ , mamy ${\ Displaystyle \ theta (\ eta, 0) = 0}$ i dla ${\ Displaystyle \ tau > 0}$ θ $\ displaystyle \ theta}$ musi spełniać ${\ Displaystyle \ theta (1, \ tau) = 0}$ i ${\ Displaystyle \ częściowe \ teta / \ częściowe \ eta | _ {\ eta = 0} = 0.}$

Teoria Semenowa

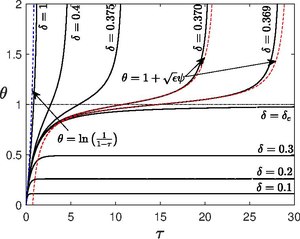
Rozwiązanie problemu Semenowa

Przed Frankiem-Kamenetskim jego promotor Nikołaj Siemionow (lub Siemionow) zaproponował teorię eksplozji termicznej z prostszym modelem, w którym przyjął funkcję liniową dla procesu przewodzenia ciepła zamiast operatora Laplaca . Równanie Semenova brzmi jak

${\ Displaystyle {\ Frac {d \ teta} {d \ tau}} = e ^ {\ teta} - {\ Frac {\ teta} {\ delta }},\quad \theta (0)=0}$

w którym wyraz wykładniczy $wzrostu$$\ displaystyle \ theta}$ do wzrostu upływu czasu, podczas gdy wyraz liniowy będzie miał tendencję ${$ mają tendencję do zmniejszania się ${\ displaystyle \ theta}$ . Odpowiednie znaczenie między tymi dwoma terminami określa liczba Damköhlera ${\ displaystyle \ delta}$ . Numeryczne rozwiązanie powyższego równania dla różnych wartości $.$ na rysunku

Reżim stały

Kiedy $→$ system jest w stanie osiągnąć stan ustalony, gdy $infty }$$tau \ rightarrow$ . W stanie ustalonym ( ${\ Displaystyle d \ theta / d \ tau = 0}$ ) równowaga jest określona równaniem

${\ Displaystyle \ delta e ^ {\ teta} = \ teta, \ quad \ Strzałka w prawo \ quad \ teta = - W (- \ delta)}$

gdzie reprezentuje funkcję $W.$ _ Z właściwości funkcji Lamberta W łatwo zauważyć, że temperatura w stanie ustalonym zapewniona przez powyższe równanie istnieje tylko wtedy, gdy $}$${\ Displaystyle \ delta \ równoważnik \ delta _ {c} = 1/$$,$ , gdzie jest nazywany parametrem -Kamenetskiego jako punkt krytyczny w którym system rozgałęzia się od stanu ustalonego do stanu wybuchowego w dużych odstępach czasu.

Wybuchowy reżim

Dla $upływu$ system eksploduje, ponieważ w miarę $wybuchnie$ długo czekać, aż . Z powodu wymuszenia wykładniczego przy skończonej wartości ${\ displaystyle \ theta \ rightarrow \$$}$ . Czas ten jest interpretowany jako czas zapłonu lub czas indukcji układu. Gdy $do {\ Displaystyle \ delta \ gg \ delta _ {c}}$ , termin przewodzenia ciepła można pominąć ${\ Displaystyle - \ theta / \ delta}$ takim przypadku problem dopuszcza wyraźne rozwiązanie ,

${\ Displaystyle {\ Frac {d \ teta} {d \ tau}} = e ^ {\ teta}, \ quad \ Strzałka w prawo \ quad \theta =\ln \left({\frac {1}{1-\tau}}\right)}$

W $_$ system Ten czas jest również nazywany okresem indukcji adiabatycznej, $zaniedbany$ składnik jest

W stanie prawie krytycznym, tj. Kiedy $.$ dużo czasu, Analiza tego limitu została po raz pierwszy przeprowadzona przez Franka-Kamenetskii, chociaż właściwe asymptotyki zostały przeprowadzone dopiero później przez DR Kassoy i Amable Liñán, w tym zużycie reagentów, ponieważ zużycie reagentów nie jest pomijalne, gdy ${\ Displaystyle \ tau \ sim \beta \gamma }$ . Poniżej przedstawiono uproszczoną analizę bez zużycia reagentów. Zdefiniujmy mały parametr $)$ , że $)}$$\ Displaystyle \ delta = \ delta _ {c} (1+$ . $delta _ {c}}$ tym przypadku ewolucja w czasie $do {\ Displaystyle \ delta =$ następująca: najpierw wzrasta do wartości temperatury w stanie ustalonym odpowiadającej , czyli \ θ $= -W (- \ delta _ {c}) = 1}$ w czasach porządku ${\ Displaystyle \ tau \ sim O(1)}$ , wtedy pozostaje bardzo blisko tej ustalonej wartości przez długi czas, zanim ostatecznie eksploduje przez długi czas. Wielkość zainteresowania jest długoterminowym oszacowaniem eksplozji. Aby znaleźć oszacowanie, wprowadź przekształcenia $i$ θ $sqrt {\ epsilon}} \ psi (\ zeta) - \ epsilon}, który$$\ Displaystyle \$$displaystyle$ jest odpowiedni dla regionu, w którym pozostaje blisko $1}$ do rządzącego równania i zbiera tylko wiodące -Zamów warunki, aby się dowiedzieć

${\ Displaystyle \ delta _ {c} {\ Frac {d \ psi}} {d \ zeta} }=1+{\frac {\psi ^{2}}{2}},\quad \psi (0)\rightarrow -(1-\theta)/{\sqrt {\epsilon}}=-\infty}$

gdzie warunek brzegowy jest uzyskiwany przez dopasowanie do początkowego regionu, w którym ${\ Displaystyle \ tau, \ theta \ sim 1}$ . Rozwiązanie powyższego problemu podaje tzw

${\ Displaystyle \ psi = - {\ sqrt {2}} \ łóżeczko \ lewo ({\ Frac {\ zeta} {{\ sqrt {2}} \ delta _ { c}}}\prawo)}$

co natychmiast ujawnia, że ​​kiedy ${\ displaystyle \ zeta = {\ sqrt {2}} \ pi \ delta _ {c}.}$$}$ Pisząc ten warunek w kategoriach , czas wybuchu w stanie prawie krytycznym wynosi ${\ displaystyle \ tau}$

${\ Displaystyle \ tau = {\ sqrt {\ Frac {2 \ pi ^ {2} \ delta _ {c} ^ {3}} {\ delta - \ delta _ {C}}}}}$

$\ delta - \ delta _ {c} \ rightarrow 0 ^ {+}$ że ​​czas zapłonu jako $Displaystyle$ kwadratem- osobliwość korzenia.

Teoria stanu ustalonego Franka-Kameneckiego

Jedynym parametrem charakteryzującym eksplozję jest liczba Damköhlera ${\ displaystyle \ delta}$ . Kiedy $wysoki$ , czas przewodzenia jest dłuższy niż czas reakcji chemicznej, a system eksploduje z wysoką temperaturą, ponieważ nie ma wystarczająco dużo czasu na przewodzenie, aby usunąć ciepło Z drugiej strony, gdy jest bardzo $niski , czas przewodzenia ciepła jest znacznie szybszy niż czas reakcji chemicznej, tak że całe ciepło wytwarzane w wyniku reakcji chemicznej jest natychmiast kierowane$ ściany, a zatem nie ma wybuchu, przechodzi do stanu prawie ustalonego, Amable Liñán ukuł ten tryb jako tryb wolno reagujący. Przy krytycznej liczbie Damköhlera $przechodzi$ z trybu wolno reagującego do trybu wybuchowego Dlatego , $stanie$ jest Zamiast rozwiązać pełny problem znalezienia tego $-$ Kamenetskii rozwiązał problem stanu ustalonego dla różnych liczb Damköhlera aż do wartości krytycznej, powyżej której nie istnieje żadne stałe rozwiązanie. Więc problem do rozwiązania jest

${\ Displaystyle {\ Frac {1} {\ eta ^ {j}}} {\ Frac {d} {d \ eta}} \ left(\eta ^{j}{\frac {d\theta }{d\eta }}\right)=-\delta e^{\theta }}$

z warunkami brzegowymi

${\ Displaystyle \ teta (1) = 0, \ quad {\ Frac {d \ teta} {d \ eta}} _ {\ eta = 0} = 0}$

drugi warunek wynika z symetrii naczynia. Powyższe równanie jest szczególnym przypadkiem równania Liouville-Bratu-Gelfanda w matematyce .

Naczynie płaskie

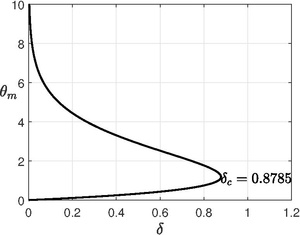
Wybuch Franka-Kameneckiego dla naczynia płaskiego

W przypadku naczynia płaskiego istnieje dokładne rozwiązanie. Tutaj zatem ${\ displaystyle j = 0}$

${\ Displaystyle {\ Frac {d ^ {2} \ teta} {d \ eta ^ {2}}} = - \ delta e ^ {\ teta}}$

${\ Displaystyle \ Theta = \ theta _ {m} - \ theta}$ i ξ ${m}} \ eta ^ {2}}$$\ Displaystyle \ xi ^ {2} = \ delta e ^ { \ theta$${\ displaystyle \ theta _ {m}$ , gdzie maksymalną temperaturą, która występuje przy symetrii, to $}$ wprowadzony

${\ Displaystyle {\ Frac {d ^ {2} \ Theta} {d \ xi ^ {2}}} = e ^{-\Theta},\quad \Theta (0)=0,\quad {\frac {d\Theta}}{d\xi}}_{\xi =0}=0}$

Całkując raz i używając drugiego warunku brzegowego, otrzymujemy równanie

${\ Displaystyle {\ Frac {d \ Theta} {d \ xi}} = {\ sqrt {2 (1-e ^ {- \ Theta})}}}$

i znowu integracja

${\ Displaystyle e ^ {(\ teta _ {m} - \ teta)/2} = \ cosh \ lewo (\ eta {\ sqrt {\frac {\delta e ^{\theta _{m}}}{2}}}\right)}$

Powyższe równanie jest dokładnym rozwiązaniem, ale maksymalna temperatura jest nieznana, ale $nie$ jeszcze warunku brzegowego ściany $\ displaystyle \ theta =$ warunek brzegowy ściany w temperatura jest uzyskiwana z wyrażenia niejawnego, θ $0}$

${\ Displaystyle e ^ {\ teta _ {m}/2} = \ cosh { \sqrt {\frac {\delta e^{\theta _{m}}}{2}}}\quad {\text{or}}\quad \delta =2e^{-\theta _{m}}\ left(\operatorname {arcosh} e^{\theta _{m}/2}\right)^{\!2}}$

Krytyczny uzyskuje się $} = 0}$ znalezienie maksymalnego punktu równania (patrz rysunek), tj. $re$$\ Displaystyle d \ delta / d \ theta _ {$ w ${\ Displaystyle \ delta _ {c}}$ .

${\ Displaystyle {\ Frac {d \ delta}} {d \ theta _ { m}}}=0,\quad \strzałka w prawo \quad e^{\theta _{m,c}/2}-{\sqrt {e^{\theta _{m,c}}-1}}\nazwa operatora {arcosh} e ^ {\ theta _ {m, c}/2} = 0}$

${\ Displaystyle \ theta _ {m, c} = 1,1868 \ quad \ Strzałka w prawo \quad \delta _{c}=0,8785}$

Tak więc krytycznym parametrem Franka-Kamentskiego jest ${\ Displaystyle \ delta _ {c} = 0,8785}$ . System nie ma stanu ustalonego (lub eksploduje) dla ${ c}=0,8785}$ { $delta$ , układ przechodzi w stan ustalony z bardzo powolną reakcją.

Naczynie cylindryczne

Wybuch Franka-Kameneckiego dla naczynia cylindrycznego

W przypadku naczynia cylindrycznego istnieje dokładne rozwiązanie. Chociaż Frank-Kamentskii zastosował całkowanie numeryczne, zakładając, że nie ma wyraźnego rozwiązania, Paul L. Chambré dostarczył dokładne rozwiązanie w 1952 r. H. Lemke rozwiązał również rozwiązanie w nieco innej formie w 1913 r. Tutaj j = 1 { $= 1}$ , więc

${\ Displaystyle {\ Frac {1} {\ eta}} {\ Frac {d} {d \ eta}} \ lewo (\ eta {\ frac {d\theta }{d\eta }}\right)=-\delta e^{\theta }}$

ω $\ theta / d \ eta}$${\ Displaystyle \ chi = e ^ {\ theta} \ eta ^ { 2}}$ i są wprowadzane

${\ Displaystyle {\ Frac {d \ omega} {d \ chi}} = - {\ Frac {\ delta} {2+ \ omega}} \ czworokąt \omega (0)=0}$

Ogólne rozwiązanie to ${\ Displaystyle \ omega ^ {2} + 4 \ omega + C = - 2 \ delta \ chi}$ . Ale z warunku symetrii w środku do ${\ displaystyle C = 0}$ Zapisując z powrotem pierwotną zmienną, równanie brzmi:

${\ Displaystyle \ eta ^ {2} \ lewo ({\ Frac {d \ teta}} {d \ eta}} \right)^{2}+4\eta {\frac {d\theta }{d\eta }}=-2\delta \eta ^{2}e^{\theta }}$

Ale oryginalne równanie pomnożone przez ${\ Displaystyle 2 \ eta ^ {2}}$

${\ Displaystyle 2 \ eta ^ {2} {\ Frac {d ^ {2} \ teta} {d \ eta ^{2}}}+2\eta {\frac {d\theta}}{d\eta}}=-2\delta \eta ^{2}e^{\theta}}$

Teraz odjęcie dwóch ostatnich równań od siebie prowadzi do

${\ Displaystyle {\ Frac {d ^ {2} \ teta} {d \ eta ^ {2}}} - {\frac {1}{\eta }}{\frac {d\theta}}{d\eta}}-{\frac {1}{2}}\left({\frac {d\theta}{d\ eta }}\right)^{2}=0}$

To równanie jest łatwe do rozwiązania, ponieważ obejmuje tylko pochodne, więc pozwalając przekształcić równanie ${\ Displaystyle g (\ eta) = d \ theta / d \ eta}$

${\ Displaystyle {\ Frac {dg} {d \ eta}} - {\ Frac {g} {\ eta}} - {\ Frac {g ^ {2}$

To jest $równanie$ różniczkowe Bernoulliego , rodzaj równania Riccatiego . Rozwiązaniem jest

${\ Displaystyle g (\ eta) = {\ Frac {d \ teta} {d \ eta}} = - {\ Frac {4 \ eta }{B'+\eta ^{2}}}}$

Całkując ponownie, mamy ${\ Displaystyle \ theta = A-2 \ ln (B \ eta ^ {2} + 1)}$ gdzie ${\ Displaystyle B = 1 / B'}$ . Użyliśmy już jednego warunku brzegowego, pozostał jeszcze jeden warunek brzegowy, ale z dwiema stałymi. ${\ displaystyle A, \ B}$ . Okazuje się, $ZA$ i $displaystyle A=\ln(8B/\delta )}$ ze sobą powiązane, co uzyskuje się przez podstawienie powyższego rozwiązania do wyjściowego równania, do którego dochodzimy $=$ . Dlatego rozwiązaniem jest

${\ Displaystyle \ teta = \ ln {\ Frac {8B / \ delta} {(B \ eta ^ {2} + 1) ^ {2}} }}$

Teraz, jeśli użyjemy drugiego warunku brzegowego $Displaystyle$ równanie dla $B$$\ styl wyświetlania \delta (B+1)^{2}-8B=0}$ jako . Maksymalna wartość, dla której możliwe jest rozwiązanie, jest wtedy, gdy $,$$do$ krytycznym parametrem Franka-Kamentskii jest ${c} =2}$ . System nie ma stanu ustalonego (lub eksploduje) dla ${ c}=2}$ δ $\$ , system przechodzi w stan ustalony z bardzo powolną reakcją. Maksymalna temperatura występuje przy ${\ displaystyle \ theta _ {m}}$${\ displaystyle \ eta = 0}$

${\ Displaystyle \ teta _ {m} = \ ln {\ Frac {8B} {\ delta}} \ quad {\ tekst {lub}}$

Dla każdej wartości $θ$ dwie wartości $displaystyle \ theta _ {m$$},$ ponieważ jest wielowartościowy. Maksymalna temperatura krytyczna wynosi ${\ Displaystyle \ theta _ {m, c} = \ ln 4}$ .

Sferyczne naczynie

Naczynie kuliste Franka-Kamienieckiego

Dla naczynia kulistego nie ma znanego jednoznacznego rozwiązania, więc Frank-Kameneckii użył metod numerycznych, aby znaleźć wartość krytyczną. Tutaj zatem ${\ displaystyle j = 2}$

${\ Displaystyle {\ Frac {1} {\ eta ^ {2}}} {\ Frac {d} {d \ eta}} \ left(\eta ^{2}{\frac {d\theta }{d\eta }}\right)=-\delta e^{\theta }}$

${\ Displaystyle \ Theta = \ theta _ {m} - \ theta}$ i ξ ${m}} \ eta ^ {2}}$$\ Displaystyle \ xi ^ {2} = \ delta e ^ { \ theta$${\ displaystyle \ theta _ {m}$ , gdzie maksymalną temperaturą, która występuje przy symetrii, to $}$ wprowadzony

${\ Displaystyle {\ Frac {1} {\ xi ^ {2}}}} \frac {d}{d\xi }}\left(\xi ^{2}{\frac {d\Theta }{d\xi }}\right)=e^{-\Theta },\quad \Theta (0)=0,\quad {\frac {d\Theta}}{d\xi}}_{\xi =0}=0}$

Powyższe równanie to nic innego jak równanie Emdena-Chandrasekhara , które pojawia się w astrofizyce opisującej izotermiczną kulę gazową. ${\ Displaystyle \ delta <\ delta _ {c$ cylindrycznego, naczynie sferyczne ma nieskończenie wiele rozwiązań dla wokół punktu zamiast tylko $}$ dwa rozwiązania, które przedstawił Israel Gelfand . Najniższa gałąź zostanie wybrana do wyjaśnienia wybuchowego zachowania.

Z rozwiązania numerycznego wynika, że ​​​​krytyczny parametr Franka-Kameneckiego wynosi ${\ Displaystyle \ delta _ {c} = 3,3220}$ . System nie ma stanu ustalonego (lub eksploduje) dla $_$ 3,3220 $Displaystyle$ , układ przechodzi w stan ustalony z bardzo powolną reakcją. Maksymalna temperatura występuje przy $}},$$theta _ {$$1,6079}$ a maksymalna temperatura krytyczna wynosi ${\ Displaystyle \ theta _ {m, c}$ .

Geometrie niesymetryczne

W przypadku naczyń, które nie są symetryczne względem środka (na przykład naczynia prostokątnego), problem polega na rozwiązaniu nieliniowego równania różniczkowego cząstkowego zamiast nieliniowego równania różniczkowego zwyczajnego , które w większości przypadków można rozwiązać tylko metodami numerycznymi. Równanie jest

${\ Displaystyle \ nabla ^ {2} \ teta + \ delta e ^ {\ teta} = 0}$

z warunkiem brzegowym na powierzchniach ograniczających ${\ displaystyle \ theta = 0}$

Aplikacje

Ponieważ model zakłada jednorodną mieszaninę, teoria ma zastosowanie do badania wybuchowego zachowania paliw stałych (spontaniczny zapłon biopaliw, materiałów organicznych, śmieci itp.). Jest to również wykorzystywane do projektowania materiałów wybuchowych i petard. Teoria dokładnie przewidywała wartości krytyczne dla płynów/ciał stałych o niskim przewodnictwie za pomocą cienkościennych pojemników o wysokiej przewodności.

Zobacz też

• Równanie Clarke'a

Linki zewnętrzne

• Problem Franka-Kamenetskiego w rozwiązaniu Wolframa http://demonstrations.wolfram.com/TheFrankKamenetskiiProblem/
• Śledzenie problemu Franka-Kamenetskiego w rozwiązaniu Wolfram http://demonstrations.wolfram.com/TrackingTheFrankKamenetskiiProblem/
• Planarne rozwiązanie w rozwiązaniu Chebfun http://www.chebfun.org/examples/ode-nonlin/BlowupFK.html