Witalij obejmujący lemat

W matematyce lemat obejmujący Vitali jest wynikiem kombinatorycznym i geometrycznym powszechnie używanym w teorii miary przestrzeni euklidesowych . Ten lemat jest etapem pośrednim, o niezależnym znaczeniu, w dowodzie twierdzenia Vitali'ego obejmującego . Twierdzenie o pokryciu przypisuje się włoskiemu matematykowi Giuseppe Vitali . Twierdzenie stwierdza, że ​​możliwe jest pokrycie, z dokładnością do zbioru Lebesgue'a , danego podzbioru E z R ^d przez rozłączną rodzinę wyodrębnioną z pokrycia Vitali E.

Witalij obejmujący lemat

Wizualizacja lematu w ${\ Displaystyle \ mathbb {R} ^ {1}}$ .

Na górze: kolekcja piłek; zielone kule to podkolekcja rozłączna. Na dole: podkolekcja o trzykrotnym promieniu obejmuje wszystkie kulki.

Istnieją dwie podstawowe wersje lematu, wersja skończona i wersja nieskończona. Oba lematy można udowodnić w ogólnym ustawieniu przestrzeni metrycznej , zazwyczaj wyniki te są stosowane do szczególnego przypadku przestrzeni euklidesowej ${\ displaystyle \ mathbb {R} ^ {d}}$ . $c$$in \$ użyjemy następującej notacji: jeśli { \ mathbb dla piłki napiszemy $r$${\ textstyle B (x, cr$ )

Wersja skończona

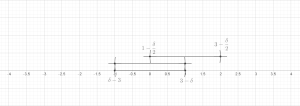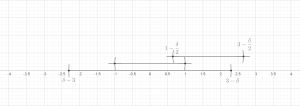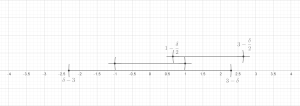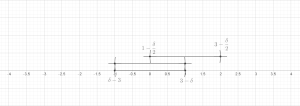
Twierdzenie (lemat o skończonych pokryciach). Niech $będzie$ zawartych dowolnej . Wtedy istnieje podkolekcja ${\ Displaystyle B_ {j_ {1}}, B_ {j_ {2}}, \ kropki, B_ {j_ {m}}}$ tych kule, które są rozłączne i spełniają

$${\ Displaystyle B_ {1} \ kubek B_ {2} \ kubek \ kropki \ kubek B_ {n} \ subseteq 3B_ {j_ {1}} \ kubek 3B_ {j_ {2}} \ kubek \ kropki \ kubek 3B_ {j_ {M}}.}$$

Dowód: Bez utraty ogólności zakładamy, że zbiór kul nie jest pusty; $to$ znaczy n > 0. Niech największym promieniu. Indukcyjnie załóżmy, że wybrano ${\ Displaystyle B_ {j_ {1}}, \ kropki, B_ {j_ {k}}} .$ Jeśli jest jakaś piłka w ${\ Displaystyle B_ {1}, \ kropki, B_ {n}}$ to jest rozłączne z ${\ Displaystyle B_ {j_ {1}} \ kubek B_ {j_ {2}} \ kubek \ kropki \ kubek B_ {j_ {k}}}$ , niech będzie taką piłką o maksymalnym promieniu $) ,$ razie ustawiamy m : = i definicję indukcyjną.

Teraz ustaw ${\ textstyle X: = \ bigcup _ {k = 1} ^ {m} 3 \, B_ {j_ {k}}}$ . Pozostaje pokazać, że dla każdego $ja$$i = 1,2, \ kropki,$ { Jest to jasne, jeśli ${\ Displaystyle i \ w \ {j_ {1}, \ kropki, j_ {m} \}}$ . W przeciwnym razie koniecznie jest jakiś taki, że przecina się ${\ Displaystyle k \$$}}},$${ i}}$ przecina się $\ {1, \ kropki, m \}} displaystyle$$a$ promień jest co najmniej tak duży jak promień ${\ displaystyle B_ {i}}$ . The nierówność trójkąta łatwo implikuje wtedy, że ${\ Displaystyle B_ {i} \ podzbiór 3 \, B_ {j_ {k}} \ podzbiór X}$ , w razie potrzeby. To kończy dowód skończonej wersji.

Wersja nieskończona

Twierdzenie (lemat o nieskończonym pokryciu). Niech będzie dowolnym zbiorem piłek w rozdzielnej przestrzeni metrycznej takiej, że ${\ displaystyle \ mathbf {F}}$

$${\ Displaystyle R: = \ sup \, \ {\ operatorname {rad} (B): B \ w \ mathbf {F} \}< \infty}$$

gdzie ${\ Displaystyle \ operatorname {rad} (B)}$ oznacza promień piłki B . Wtedy istnieje $F}}$ podzbiór taki, że kule są parami rozłączne i spełniają sol ${$

$${\ Displaystyle \ bigcup _ {B \ in \ mathbf {F}} B \ subseteq \ bigcup _ {C \ in \ mathbf {G}} 5 \, C.}$$

$\ in \$ więcej, każdy przecina jakiś czas $.$ b $}$ mathbf

Dowód: Rozważmy podział F na podzbiory F _n , n ≥ 0, określone przez

${\ Displaystyle \ mathbf {F} _ {n} = \ {B \ w \ mathbf {F}: 2 ^ {-n-1} R <{\ tekst {rad}} (B) \ równoważnik 2 ^ {- n}R\}.}$

₀₀₀₀$że$ to, składa się z kulek B , promień wynosi (2 ^{- n -1} R , 2 ^{- n} R ). Sekwencja G _n , gdzie G _n ⊂ F _n , jest zdefiniowane indukcyjnie w następujący sposób: Najpierw ustalmy H = F i niech G będzie maksymalnym rozłącznym podzbiorem H (taki podzbiór istnieje na mocy lematu Zorna ₀ ). Zakładając, że wybrano G ,…, G _{n , niech}

${\ Displaystyle \ mathbf {H} _ {n + 1} = \ { B\in \mathbf {F} _{n+1}:\ B\cap C=\pusty zbiór ,\ \ \forall C\in \mathbf {G} _{0}\cup \mathbf {G} _{1 }\cup \dots \cup \mathbf {G} _{n}\},}$

i niech G _{n +1} będzie maksymalnym rozłącznym podzbiorem H _{n +1} . Podkolekcja

${\ Displaystyle \ mathbf {G}: = \ bigcup _ {n = 0} ^ {\ infty} \ mathbf {G} _ {n}}$

z F spełnia wymagania twierdzenia: G jest zbiorem rozłącznym, a zatem jest przeliczalny, ponieważ dana przestrzeń metryczna jest separowalna. Ponadto każda kula B ∈ F przecina kulę C ∈ G taką, że B ⊂ 5 C . Rzeczywiście , jeśli otrzymamy jakieś $musi$ istnieć jakieś n takie, B do fa _{n 00} . Albo B nie należy do H _n , co implikuje n > 0 i oznacza, że ​​B przecina kulę ze sumy G , …, G _{n −1} , albo B ∈ H _n i przez maksymalizację G _n , B przecina kulę w Gn . _{_} W każdym razie B przecina kulę C , która należy do sumy G , …, G _rz . Taka kula C musi mieć promień większy niż 2 ^{− n −1} R . Ponieważ promień B jest mniejszy lub równy 2 ^{− n} R, możemy wywnioskować z nierówności trójkąta, że ​​B ⊂ 5 C, jak twierdzono. Z tego ${\ Displaystyle \ bigcup _ {B \ w \ mathbf {F}} B \ subseteq \ bigcup _ {C \ w \ mathbf {G}} 5 \, C }$ natychmiast następuje, kończąc dowód.

Uwagi

• W wersji nieskończonej początkowy zbiór piłek może być policzalny lub niepoliczalny . W rozdzielnej przestrzeni metrycznej każdy parami rozłączny zbiór piłek musi być policzalny. W przestrzeni nierozdzielnej ten sam argument pokazuje, że istnieje podrodzina rozłączna parami, ale ta rodzina nie musi być policzalna.
• Wynik może się nie powieść, jeśli promienie nie są ograniczone: rozważmy rodzinę wszystkich piłek wyśrodkowanych w 0 w R ^d ; każda rozłączna podrodzina składa się tylko z jednej kuli B , a 5 B nie zawiera wszystkich kul z tej rodziny.
• Stała 5 nie jest optymalna. Jeśli skala c ^{− n} , c > 1 zostanie użyta zamiast 2 ^{− n} do zdefiniowania F _n , ostateczna wartość to 1 + 2 c zamiast 5. Każda stała większa niż 3 daje poprawne sformułowanie lematu, ale nie 3.
• Stosując dokładniejszą analizę, gdy oryginalny zbiór F jest pokryciem Vitaliego podzbioru E z R ^d , można wykazać, że podzbiór G , zdefiniowany w powyższym dowodzie, obejmuje E aż do zbioru pomijalnego Lebesgue'a.

Zastosowania i sposób użycia

Zastosowanie lematu Vitali polega na udowodnieniu maksymalnej nierówności Hardy'ego-Littlewooda . $-$ lemat Vitali jest często , gdy na przykład rozważamy d wymiarową miarę Lebesgue'a , zbioru mi ⊂ R ^d , który znamy zawiera się w związku pewnego zbioru kulek ${\ Displaystyle \ {B_ {j}: j \ w J \}}$ , z których każdy ma miarę, którą możemy łatwiej obliczyć, lub ma specjalną właściwość, którą chcielibyśmy wykorzystać. Stąd, jeśli obliczymy miarę tego związku, będziemy mieli górną granicę miary E . Jednak trudno jest obliczyć miarę sumy wszystkich tych piłek, jeśli zachodzą na siebie. lematem Witalija możemy wybrać zbiór $,$ jest ${\ textstyle \ bigcup _ {j \ w J'} 5B_ {j} \ supset \ bigcup _ {j \ w J} B_ {j} \ supset E}$ . Dlatego,

${\ Displaystyle \ lambda _ {d} (E) \ równoważnik \ lambda _ {d} {\ biggl (} \ bigcup _ {j \ w J} B_ {j} {\ biggr )} \ równoważnik \ lambda _ {d }{\biggl (}\bigcup _{j\in J'}5B_{j}{\biggr )}\leq \sum _{j\in J'}\lambda _{d}(5B_{j}). }$

Teraz, ponieważ zwiększenie promienia d -wymiarowej kuli pięciokrotnie zwiększa jej objętość o współczynnik 5 ^d , wiemy, że

${\ Displaystyle \ suma _ {j \ w J'} \ lambda _ {d} (5B_ {j} )=5^{d}\suma _{j\w J'}\lambda _{d}(B_{j})}$

a zatem

${\ Displaystyle \ lambda _ {d} (E) \ równoważnik 5 ^ {d} \ suma _ {j \ w J '} \ lambda _ {d} (B_ {j}).}$

Twierdzenie Witalija o pokryciu

W twierdzeniu o pokryciu celem jest pokrycie, aż do „nieistotnego zbioru”, danego zbioru mi ⊆ R ^d przez rozłączny podzbiór wyodrębniony z pokrycia Vitali dla E : klasa Vitali lub pokrycie Vitali ${\ displaystyle {\ mathcal {V}}}$ dla E jest takim zbiorem zbiorów, że dla każdego x ∈ E i δ > 0 istnieje zbiór U w zbiorze \ $Displaystyle {\ mathcal {V}}}$ takie, że x ∈ U i średnica U jest niezerowa i mniejsza niż δ .

W klasycznym układzie Vitali pomijalny zbiór jest zbiorem pomijalnym Lebesgue'a , ale uwzględniono również miary inne niż miara Lebesgue'a i przestrzenie inne niż R ^{d , jak pokazano w odpowiedniej sekcji poniżej.}

Przydatna jest następująca obserwacja: jeśli $jest$ pokryciem Vitali dla E i jeśli jest zawarte w zbiorze otwartym Ω ⊆ R ^re , to podzbiór zbiorów U w $displaystyle {\mathcal {V}}}$ \ zawarte w Ω jest również pokryciem Vitaliego dla E .

Twierdzenie Witalija o pokryciu miary Lebesgue'a

Kolejne twierdzenie obejmujące miarę Lebesgue'a λ _d pochodzi od Lebesgue'a (1910) . Zbiór mierzalnych podzbiorów R ^d jest rodziną regularną (w sensie Lebesgue'a ), jeśli istnieje stała C taka, że ${\ displaystyle {\ mathcal {V}}}$

${\ Displaystyle \ nazwa operatora {średnica} (V) ^ {d} \ równoważnik C \, \ lambda _ {d} (V)}$

dla każdego zestawu V w kolekcji ${\ displaystyle {\ mathcal {V}}}$ . Rodzina kostek jest przykładem zwykłej rodziny $}$ jak rodzina R ² $}$ taki, że stosunek boków pozostaje między m ⁻¹ a m , dla pewnego ustalonego m ≥ 1. Jeśli na R ^d podana jest dowolna norma , kolejnym przykładem jest rodzina kul dla metryki powiązanej z normą. Wręcz przeciwnie, rodzina wszystkich prostokątów w R ² nie jest regularna.

Twierdzenie - Niech mi ⊆ R ^d będzie mierzalnym zbiorem ze skończoną miarą Lebesgue'a i niech $będzie$ regularną rodziną zamkniętych podzbiorów R ^d , która jest pokryciem Vitaliego E . Wtedy istnieje skończony lub przeliczalnie nieskończony rozłączny podzbiór taki, że ${\ Displaystyle \ {U_ {j} \} \ subseteq {\ mathcal {V}}}$

$${\ Displaystyle \ lambda _ {d} {\ biggl (} E \ setminus \ bigcup _ {j} U_ {j} {\ biggr)} = 0.}$$

Oryginalny wynik Vitali $1908$ ) jest szczególnym przypadkiem tego twierdzenia, w którym jest zbiorem przedziałów, który jest pokryciem Vitalego dla mierzalnego podzbioru E z linia rzeczywista mająca skończoną miarę. Powyższe twierdzenie pozostaje prawdziwe bez założenia, że ​​E ma skończoną miarę. Uzyskuje się to przez zastosowanie wyniku pokrycia w przypadku miary skończonej, dla każdej liczby całkowitej n ≥ 0, do części E zawartej w otwartym pierścieniu Ω _n punktów x takich, że n < | x | < n +1.

Nieco pokrewnym twierdzeniem o pokryciu jest twierdzenie Besicovitcha o pokryciu . Do każdego punktu a podzbioru A ⊆ R ^d przypisana jest kula euklidesowa B ( a , r _a ) o środku a i dodatnim promieniu r _{a .} Następnie, podobnie jak w twierdzeniu Vitalego, wybiera się podzbiór tych kulek, aby pokryć A w określony sposób. Główne różnice w stosunku do twierdzenia Vitalego obejmującego polegają na tym, że z jednej strony wymóg rozłączności Vitali jest złagodzony do faktu, że liczba N _x wybranych kul zawierających dowolny punkt x ∈ R ^d jest ograniczona przez stałą B _d zależną tylko na wymiar d ; z drugiej strony wybrane kule pokrywają zbiór A wszystkich podanych centrów.

Twierdzenie Witalija o pokryciu miary Hausdorffa

Podobny cel można mieć, rozważając miarę Hausdorffa zamiast miary Lebesgue'a. W takim przypadku obowiązuje następujące twierdzenie.

Twierdzenie - Niech H ^s oznacza s - wymiarową miarę Hausdorffa , niech $mi$ ⊆ R d ^będzie zbiorem H s - mierzalnym i klasą ^Vitali zbiorów domkniętych dla . Wtedy istnieje (skończony lub policzalnie nieskończony) rozłączny podzbiór taki, że ${\ Displaystyle \ {U_ {j} \} \ subseteq {\ mathcal {V}}}$

$${\ Displaystyle H ^ {s} \ lewo (E \ setminus \ bigcup _ {j} U_ {j} \ prawej) = 0}$$

Lub

$${\ Displaystyle \ suma _ {j} \ nazwa operatora {średnica} (U_ {j}) ^ {s} = \ infty.}$$

Ponadto, jeśli E ma skończoną s -wymiarową miarę Hausdorffa, to dla dowolnego ε > 0 możemy wybrać ten podzbiór { U _j } taki, że

${\ Displaystyle H ^ {s} (E) \ równoważnik \ suma _ {j} \ operatorname {diam} (U_ {j}) ^ {s} + \ varepsilon.}$

Twierdzenie to implikuje wynik Lebesgue'a podany powyżej. ^{Rzeczywiście ,} gdy s = d , miara Hausdorffa Hs na Rd pokrywa się z wielokrotnością d -wymiarowej miary Lebesgue'a. Jeśli $jest$ zbiór regularny i zawarty w mierzalnym regionie B ze , to

${\ Displaystyle \ suma _ {j} \ nazwa operatora {średnica} (U_ {j}) ^ {d}\równoważnik C\sum _{j}\lambda _{d}(U_{j})\równoważnik C\,\lambda _{d}(B)<+\infty}$

co wyklucza drugą możliwość w pierwszym stwierdzeniu poprzedniego twierdzenia. Wynika z tego, że E jest objęte, aż do zbioru pomijalnego Lebesgue'a, przez wybrany rozłączny podzbiór.

Od lematu pokrywającego do twierdzenia pokrywającego

Lemat pokrywający może być użyty jako krok pośredni w dowodzie następującej podstawowej postaci twierdzenia Vitalego o pokrywaniu.

Twierdzenie — Dla każdego podzbioru E z Rd i każdego pokrycia E przez Vitali'ego zbiorem F zamkniętych kul istnieje rozłączny podzbiór G ^, który obejmuje E aż do zbioru pomijalnego Lebesgue'a.

Dowód: bez utraty ogólności można założyć, że wszystkie kule w F są niezdegenerowane i mają promień mniejszy lub równy 1. Dzięki nieskończonej postaci lematu obejmującego istnieje policzalny rozłączny podzbiór ${\ displaystyle \ mathbf {G } }$ z F takie, że każda kula B ∈ F przecina kulę C ∈ G , dla której B ⊂ 5 C . Niech r > 0 będzie dane i niech Z oznaczmy zbiór punktów z ∈ E , które nie są zawarte w żadnej kuli z G i należą do kuli otwartej B ( r ) o promieniu r , której środek znajduje się w punkcie 0. Wystarczy pokazać, że Z jest pomijalny w sensie Lebesgue'a, dla każdej danej r .

Niech ${\ Displaystyle \ mathbf {G} _ {r} = \ {C_ {n} \} _ {n}}$ oznacza podzbiór tych piłek w G , które spotykają się z B ( r ). Zauważ, że $może$ lub policzalnie nieskończony. Niech z ∈ Z będzie ustalone. Dla każdego N, z nie należy do zbioru domkniętego ${\ Displaystyle K = \ bigcup _ {n \ równoważnik N} C_ {n}}$ z definicji Z . Ale dzięki własności pokrycia Vitali'ego można znaleźć kulę B ∈ F zawierającą z , zawartą w B ( r ) i rozłączną z K . Zgodnie z właściwością G , piłka B przecina pewną piłkę $}}$$sol {\ Displaystyle C_ {i} \ in$ zawarta w . Ale ponieważ K i B są rozłączne, musimy mieć i > N. Więc dla pewnego i > N, a zatem ${\ Displaystyle z \ in 5C_ {i}}$

${\ Displaystyle Z \ podzbiór \ bigcup _ {n> N} 5C_ {n}.}$

Daje to dla każdego N nierówność

${\ Displaystyle \ lambda _ {d} (Z) \ równoważnik \ suma _ {n> N} \ lambda _ {d} (5C_ {n}) = 5 ^ {d} \ suma _ {n> N} \ lambda _{d}(C_{n}).}$

Ale ponieważ kule z są zawarte w B (r + 2) i te kule są rozłączne, widzimy, $.$

${\ Displaystyle \ suma _ {n} \ lambda _ {d} (C_ {n}) <\ infty.}$

Dlatego wyraz po prawej stronie powyższej nierówności zbiega się do 0, gdy N dąży do nieskończoności, co pokazuje, że Z jest pomijalne w razie potrzeby.

Przestrzenie nieskończenie wymiarowe

Twierdzenie o pokryciu Vitaliego nie obowiązuje w ustawieniach nieskończenie wymiarowych. Pierwszy wynik w tym kierunku dał David Preiss w 1979 r.: istnieje miara Gaussa γ na (nieskończenie wymiarowej) separowalnej przestrzeni Hilberta H , tak że twierdzenie Vitalego o pokryciu zawodzi dla ( H , Borel ( H ), γ ). Wynik ten został wzmocniony w 2003 roku przez Jaroslava Tišera: twierdzenie Vitalego o pokryciu w rzeczywistości zawodzi dla każdego nieskończenie wymiarowa miara Gaussa na dowolnej (nieskończenie wymiarowej) rozdzielnej przestrzeni Hilberta.

Zobacz też

• Twierdzenie Besicovitcha obejmujące

Notatki

•     Evans, Lawrence C.; Gariepy, Ronald F. (1992), Teoria miary i dokładne właściwości funkcji , Studies in Advanced Mathematics , Boca Raton, FL : CRC Press , s. VIII + 268, ISBN 0-8493-7157-0 , MR 1158660 , Zbl 0804.28001
•     Falconer, Kenneth J. (1986), Geometria zbiorów fraktalnych , Cambridge Tracts in Mathematics, tom. 85, Cambridge: Cambridge University Press , s. xiv+162, ISBN 0-521-25694-1 , MR 0867284 , Zbl 0587.28004
• „Twierdzenie Witalija” , Encyklopedia matematyki , EMS Press , 2001 [1994]
•   Lebesgue, Henri (1910), "Sur l'integration des funkctions przerywa" , Annales Scientifiques de l'École Normale Supérieure , 27 : 361–450, doi : 10.24033/asens.624 , JFM 41.0457.01
•    Natanson, IP (1955), Teoria funkcji zmiennej rzeczywistej , New York: Frederick Ungar Publishing Co., s. 277, MR 0067952 , Zbl 0064.29102
•     Preiss, David (1979), „Miary Gaussa i twierdzenia obejmujące”, Commentatione Mathematicae Universitatis Carolinae , 20 (1): 95–99, ISSN 0010-2628 , MR 0526149 , Zbl 0386.28015
•     Stein, Elias M .; Shakarchi, Rami (2005), Analiza rzeczywista. Teoria miary, całkowanie i przestrzenie Hilberta , Princeton Lectures in Analysis, III, Princeton, NJ : Princeton University Press, s. xx + 402, ISBN 0-691-11386-6 , MR 2129625 , Zbl 1081.28001
•    Tišer, Jaroslav (2003), „Witalij obejmujący twierdzenie w przestrzeni Hilberta”, Transactions of the American Mathematical Society , 355 (8): 3277–3289 (elektroniczny), doi : 10.1090 / S0002-9947-03-03296-3 , MR 1974687 , Zbl 1042.28014
•   Vitali, Giuseppe (1908) [17 grudnia 1907], "Sui gruppi di punti e sulle funzioni di variabili reali" , Atti dell'Accademia delle Scienze di Torino (w języku włoskim), 43 : 75–92, JFM 39.0101.05 (tytuł tłumaczenie) „ O grupach punktów i funkcjach zmiennych rzeczywistych ” to praca zawierająca pierwszy dowód twierdzenia Vitalego obejmującego .