Twierdzenie o trzech przerwach

W matematyce twierdzenie o trzech przerwach , twierdzenie o trzech odległościach lub hipoteza Steinhausa stwierdza, że jeśli umieści się $n$ punktów na okręgu pod kątami $θ$ , $2 θ$ , $3 θ$ , ... od punktu początkowego, to będzie być co najwyżej trzema różnymi odległościami między parami punktów w sąsiednich pozycjach wokół okręgu. Gdy są trzy odległości, największa z nich jest zawsze równa sumie dwóch pozostałych. Chyba że $θ$ jest wymierną wielokrotnością $π$ , będą również co najmniej dwie różne odległości.

Wynik ten został wysunięty przez Hugo Steinhausa i udowodniony w latach pięćdziesiątych przez Verę T. Sós , Jánosa Surányi [ hu ] i Stanisława Świerczkowskiego ; więcej dowodów zostało później dodanych przez innych. Zastosowania twierdzenia o trzech przerwach obejmują badanie wzrostu roślin i systemów strojenia muzycznego oraz teorię odbicia światła w lustrzanym kwadracie.

Oświadczenie

Twierdzenie o trzech przerwach można określić geometrycznie za pomocą punktów na okręgu. W tej formie stwierdza, że jeśli umieści się $okręgu$ pod kątami , ${\ Displaystyle \ theta, 2 \ theta, \ kropki, n \ theta}$ od punktu początkowego, to będą co najwyżej trzy różne odległości między parami punktów w sąsiednich pozycjach wokół okręgu. Równoważna i bardziej algebraiczna forma obejmuje części ułamkowe wielokrotności liczby rzeczywistej . Stwierdza, że dla dowolnej dodatniej liczby rzeczywistej $i$ liczby $całkowitej$ ułamkowe części liczb $\ Displaystyle \ alfa, 2 \ alfa$ dzielimy przedział jednostkowy na podprzedziały o co najwyżej trzech różnych długościach. Te dwa problemy są równoważne przy liniowej zgodności między odstępem jednostkowym a obwodem koła oraz zgodności między liczbą rzeczywistą ${\ Displaystyle \ alpha}$ i kąt ${\ Displaystyle \ theta = 2 \ pi \ alpha}$ .

Aplikacje

Wzrost rośliny

Widok końca łodygi rośliny, w którym kolejne liście są oddzielone złotym kątem

W badaniu filotaksji , ułożenia liści na łodygach roślin, zaobserwowano, że każdy kolejny liść na łodygach wielu roślin jest odwrócony od poprzedniego liścia o złoty kąt , około 137,5°. Sugerowano, że ten kąt maksymalizuje zdolność zbierania słońca przez liście rośliny. Jeśli spojrzy się od końca na łodygę rośliny, która wyrosła w ten sposób, będzie co najwyżej trzy różne kąty między dwoma liśćmi, które są następujące po sobie w cyklicznym porządku określonym przez ten widok od końca.

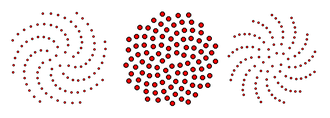
Punkty rozmieszczone pod złotym kątem wzdłuż spirali Fermata (w środku) są rozmieszczone bardziej równomiernie niż w przypadku innych kątów.

Na przykład na rysunku największy z tych trzech kątów występuje trzy razy, między liśćmi o numerach 3 i 6, między liśćmi 4 i 7 oraz między liśćmi 5 i 8. Drugi co do wielkości kąt występuje pięć razy, między liśćmi 6 i 1, 9 i 4, 7 i 2, 10 i 5 oraz 8 i 3. A najmniejszy kąt występuje tylko dwa razy, między liśćmi 1 i 9 oraz między liśćmi 2 i 10. Zjawisko posiadania trzech rodzajów wyraźnych przerw zależy tylko na fakcie, że wzorzec wzrostu wykorzystuje stały kąt obrotu, a nie na stosunku tego kąta do złotego podziału ; to samo zjawisko miałoby miejsce dla każdego innego kąta obrotu, a nie tylko dla złotego kąta. Jednak inne właściwości tego wzorca wzrostu zależą od złotego podziału. Na przykład fakt, że złoty podział jest liczbą trudną do przybliżenia, oznacza, że punkty rozmieszczone pod tym kątem wzdłuż spirali Fermata (jak to ma miejsce w niektórych modelach wzrostu roślin) tworzą zbiór Delone ; intuicyjnie oznacza to, że są równomiernie rozmieszczone.

Teoria muzyki

Tony strojenia pitagorejskiego jako punkty koła chromatycznego . Krawędzie wskazują doskonałe kwinty użyte do skonstruowania strojenia; dwie dłuższe przerwy między kolejnymi punktami reprezentują półtony , a krótka przerwa, w której dodekagram nie zamyka się, to przecinek pitagorejski .

W teorii muzyki interwał muzyczny opisuje stosunek częstotliwości między dwoma tonami muzycznymi . Odstępy są powszechnie uważane za spółgłoskowe lub harmoniczne, gdy są stosunkiem dwóch małych liczb całkowitych; na przykład oktawa odpowiada stosunkowi 2: 1, podczas gdy kwinta doskonała odpowiada stosunkowi 3: 2. Dwa tony są powszechnie uważane za równoważne, gdy różnią się o całkowitą liczbę oktaw; tę równoważność można przedstawić geometrycznie za pomocą koła chromatycznego , których punkty reprezentują klasy tonów równoważnych. Matematycznie okrąg ten można opisać jako okrąg jednostkowy na płaszczyźnie zespolonej , a punkt na tym okręgu reprezentujący dany ton można uzyskać przez odwzorowanie częstotliwości $na$ zespoloną ${\ textstyle \ exp (2 \ pi ja \ log _ {2} \ nu)}$ . Interwał ze stosunkiem ${\ displaystyle \ rho}$ odpowiada kątowi między punktami na tym okręgu, co oznacza $dwa tony muzyczne$ okręgu różnią się o ten kąt. Na przykład ten wzór daje $koło)$ jako kąt odpowiadający oktawie. Ponieważ 3/2 nie jest potęgą wymierną dwójki , kąt na kole chromatycznym reprezentujący kwintę doskonałą nie jest wymierną wielokrotnością ${\ Displaystyle 2 \ pi}$ i podobnie inne popularne interwały muzyczne inne niż oktawa nie odpowiadają racjonalnym kątom.

System strojenia to zbiór tonów używanych do komponowania i odtwarzania muzyki. Na przykład równotemperamentowy, powszechnie używany w przypadku fortepianu , to system strojenia składający się z 12 tonów równomiernie rozmieszczonych wokół koła chromatycznego. Niektóre inne systemy strojenia nie rozkładają swoich tonów równomiernie, ale zamiast tego generują je przez pewną liczbę kolejnych wielokrotności danego interwału. Przykładem jest strojenie pitagorejskie , które jest skonstruowane w ten sposób z dwunastu tonów, generowanych jako kolejne wielokrotności kwinty doskonałej w kręgu kwint . Kąt niewymierny utworzony na kole chromatycznym przez kwintę doskonałą jest bliski 7/12 koła, a zatem dwanaście tonów strojenia pitagorejskiego jest zbliżonych, ale nie tożsamych, z dwunastoma tonami o jednakowym temperamencie, które mogłyby wygenerować w ten sam sposób przy użyciu kąta równego dokładnie 7/12 koła. Zamiast być rozmieszczone pod kątem dokładnie 1/12 koła, jak byłoby w przypadku tonów o jednakowym temperamencie, tony pitagorejskiego strojenia są oddzielone interwałami dwóch różnych kątów, blisko, ale nie dokładnie 1/12 koła , reprezentujących dwa różne rodzaje półtonów . Gdyby pitagorejski system strojenia został rozszerzony o jeszcze jedną kwintę doskonałą, do zestawu 13 tonów, to sekwencja interwałów między jego tonami obejmowałaby trzeci, znacznie krótszy interwał, przecinek pitagorejski .

W tym kontekście twierdzenie o trzech przerwach może być użyte do opisania dowolnego systemu strojenia, który jest generowany w ten sposób przez kolejne wielokrotności pojedynczego przedziału. Niektóre z tych systemów strojenia (np. równotemperaturowe) mogą mieć tylko jeden interwał oddzielający najbliższe pary tonów, a niektóre (jak strojenie Pitagorasa) mogą mieć tylko dwa różne interwały oddzielające tony, ale twierdzenie o trzech przerwach implikuje, że istnieją zawsze co najwyżej trzy różne interwały oddzielające tony.

Lustrzane odbicie

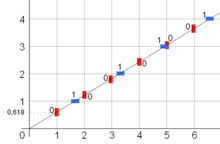
W słowie Fibonacciego , będącym przykładem słowa Sturmian , istnieją cztery różne podciągi o długości 3 (w kolejności od lewej do prawej): 010, 100, 001 i 101.

Słowo Sturmian to nieskończona sekwencja dwóch symboli (na przykład „H” i „V”) opisujących sekwencję poziomych i pionowych odbić promienia światła w lustrzanym kwadracie, zaczynając wzdłuż linii irracjonalnego nachylenia. Równoważnie ta sama sekwencja opisuje sekwencję poziomych i pionowych linii siatki liczb całkowitych, które przecina linia początkowa. Jedną z właściwości, które mają wszystkie takie sekwencje, jest to, że dla dowolnej dodatniej liczby całkowitej $n$ sekwencja ma dokładnie $n + 1$ różnych kolejnych podsekwencji o długości $n$ . Każdy podciąg występuje nieskończenie często z określoną częstotliwością, a twierdzenie o trzech przerwach implikuje, że te $n + 1$ podciągów występuje z co najwyżej trzema różnymi częstotliwościami. Jeśli są trzy częstotliwości, to największa częstotliwość musi być równa sumie dwóch pozostałych. Jeden dowód tego wyniku polega na podziale punktów przecięcia z osią $y$ linii początkowych (modulo 1) na $n + 1$ podprzedziałów, w których początkowych $n$ elementów sekwencji jest takich samych, i zastosowaniu twierdzenia o trzech przerwach do tego podziału.

Historia i dowód

Twierdzenie o trzech lukach zostało wymyślone przez Hugo Steinhausa , a jego pierwsze dowody znaleźli pod koniec lat pięćdziesiątych Vera T. Sós , János Surányi [ hu ] i Stanisław Świerczkowski . Później badacze opublikowali dodatkowe dowody, uogólniając ten wynik na wyższe wymiary i łącząc go z tematami obejmującymi ułamki ciągłe , symetrie i geodezję rozmaitości riemannowskich , teorię ergodyczną i przestrzeń płaskich krat . Mayero (2000) formalizuje dowód za pomocą interaktywnego dowodzenia twierdzeń Coq .

Poniższy prosty dowód pochodzi od Franka Lianga. Niech $θ$ będzie kątem obrotu generującym zbiór punktów jako pewną liczbę kolejnych wielokrotności $θ$ na okręgu. Zdefiniuj przerwę jako łuk $A$ okręgu, który rozciąga się między dwoma sąsiednimi punktami danego zbioru, i zdefiniuj przerwę jako sztywną , jeśli jej punkty końcowe występują później w sekwencji wielokrotności $θ$ niż jakakolwiek inna przerwa o tej samej długości. Z definicji tej wynika, że każda szczelina ma taką samą długość jak szczelina sztywna. Jeśli $A$ jest przerwą sztywną, to $A + θ$ nie jest przerwą, ponieważ ma taką samą długość i byłaby o krok później. Jedynym sposobem, aby to się stało, jest to, aby jeden z punktów końcowych $A$ był ostatnim punktem w sekwencji wielokrotności $θ (tak, że$ brakuje odpowiedniego punktu końcowego $A + θ ) lub aby jeden z podanych punktów wylądował w$ $A + θ$ , zapobiegając temu, aby był przerwą. Punkt może wylądować w $A + θ tylko$ wtedy, gdy jest pierwszym punktem w sekwencji wielokrotności $θ$ , ponieważ w przeciwnym razie jego poprzednik w sekwencji wylądowałby w $A$ , co jest sprzeczne z założeniem, że $A$ jest przerwą. Tak więc mogą istnieć co najwyżej trzy sztywne luki, dwie po obu stronach ostatniego punktu i ta, w której wylądowałby poprzednik pierwszego punktu (gdyby był częścią sekwencji). Ponieważ są co najwyżej trzy sztywne szczeliny, są co najwyżej trzy długości szczelin.

Powiązane wyniki

Dowód Lianga dodatkowo pokazuje, że gdy istnieją dokładnie trzy długości przerwy, najdłuższa długość przerwy jest sumą pozostałych dwóch. Ponieważ w tym przypadku obrócona kopia $A + θ$ , która ma w sobie pierwszy punkt, jest podzielona przez ten punkt na dwie mniejsze luki, które muszą być pozostałymi dwiema lukami. Liang udowadnia $również$ bardziej ogólny wynik, „ $odległości$ ”, zgodnie z którym suma różnych postępów arytmetycznych okręgu ma co najwyżej ${\ displaystyle 3d}$ różne długości przerw. W twierdzeniu o trzech przerwach istnieje stała granica stosunków między trzema przerwami wtedy i tylko wtedy, gdy $θ /2 π$ jest liczbą źle przybliżoną .

Ściśle spokrewnione, ale wcześniejsze twierdzenie, zwane także twierdzeniem o trzech przerwach, głosi, że jeśli $A$ jest dowolnym łukiem koła, to ciąg całkowity wielokrotności $θ$ , który ląduje w $A$ , ma co najwyżej trzy długości przerw między wartościami ciągu. Ponownie, jeśli istnieją trzy długości przerwy, to jedna jest sumą dwóch pozostałych.

Zobacz też