Wykres Desarguesa

Wykres Desarguesa
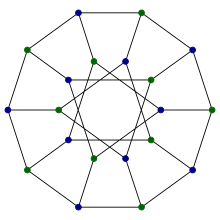Nazwany po	Gérarda Desarguesa
Wierzchołki	20
Krawędzie	30
Promień	5
Średnica	5
Obwód	6
Automorfizmy	240 ( S 5 × ℤ/2 ℤ )
Liczba chromatyczna	2
Indeks chromatyczny	3
Rodzaj	2
Grubość książki	3
Numer kolejki	2
Nieruchomości	Sześcienny regularny hamiltonian dwudzielny symetryczny
Tabela wykresów i parametrów

W matematycznej dziedzinie teorii grafów graf Desarguesa jest grafem sześciennym przechodnim na odległość z 20 wierzchołkami i 30 krawędziami. Został nazwany na cześć Girarda Desarguesa , wywodzi się z kilku różnych konstrukcji kombinatorycznych, ma wysoki poziom symetrii, jest jedynym znanym niepłaskim sześciennym sześcianem częściowym i został zastosowany w chemicznych bazach danych.

Nazwa „wykres Desarguesa” była również używana w odniesieniu do wykresu z dziesięcioma wierzchołkami, dopełnienia wykresu Petersena , który można również utworzyć jako dwudzielną połowę wykresu Desarguesa z 20 wierzchołkami.

Konstrukcje

Istnieje kilka różnych sposobów konstruowania wykresu Desarguesa:

• Jest to uogólniony graf Petersena G (10,3) . Aby utworzyć graf Desarguesa w ten sposób, połącz dziesięć wierzchołków w regularny dziesięciokąt , a pozostałe dziesięć wierzchołków w dziesięcioramienną gwiazdę, która łączy pary wierzchołków w odległości trzech w drugim dziesięciokącie. Graf Desarguesa składa się z 20 krawędzi tych dwóch wielokątów wraz z dodatkowymi 10 krawędziami łączącymi punkty jednego dziesięciokąta z odpowiednimi punktami drugiego.
• Jest to wykres Leviego konfiguracji Desarguesa . Ta konfiguracja składa się z dziesięciu punktów i dziesięciu linii opisujących dwa trójkąty perspektywiczne , ich środek perspektywy i ich oś perspektywy. Wykres Desarguesa ma jeden wierzchołek dla każdego punktu, jeden wierzchołek dla każdej linii i jedną krawędź dla każdej incydentalnej pary punkt-linia. Twierdzenie Desarguesa , nazwane na cześć XVII-wiecznego francuskiego matematyka Gérarda Desarguesa , opisuje zbiór punktów i linii tworzących tę konfigurację, a konfiguracja i wykres biorą od niej swoją nazwę.
• Jest to dwudzielna podwójna pokrywa grafu Petersena , utworzona przez zastąpienie każdego wierzchołka grafu Petersena parą wierzchołków i każdej krawędzi grafu Petersena parą krawędzi skrzyżowanych.
• Jest to dwudzielny graf Knesera H _5,2 . Jego wierzchołki mogą być oznaczone przez dziesięć podzbiorów dwuelementowych i dziesięć podzbiorów trzyelementowych zbioru pięcioelementowego, z krawędzią łączącą dwa wierzchołki, gdy jeden z odpowiednich zestawów jest podzbiorem drugiego. Równoważnie wykres Desarguesa jest indukowanym podgrafem 5-wymiarowego hipersześcianu określonego przez wierzchołki o wadze 2 i wadze 3.
• Graf Desarguesa jest hamiltonowski i można go skonstruować z notacji LCF : [5,−5,9,−9] ⁵ . Ponieważ Erdős przypuszczał, że dla k > 0 podwykres (2 k + 1) -wymiarowego hipersześcianu indukowanego przez wierzchołki o ciężarze k i k + 1 jest hamiltonowski, hamiltoniczność wykresu Desarguesa nie jest niespodzianką. (Z silniejszego przypuszczenia Lovásza wynika również, że z wyjątkiem kilku znanych kontrprzykładów, wszystkie grafy przechodnie wierzchołków mają cykle Hamiltona).

Właściwości algebraiczne

Graf Desarguesa jest grafem symetrycznym : ma symetrie, które przenoszą dowolny wierzchołek do dowolnego innego wierzchołka i dowolną krawędź do dowolnej innej krawędzi. Jego grupa symetrii ma rząd 240 i jest izomorficzna z iloczynem grupy symetrycznej w 5 punktach z grupą rzędu 2.

Można zinterpretować tę iloczynową reprezentację grupy symetrii w kategoriach konstrukcji grafu Desarguesa: grupa symetryczna na pięciu punktach jest grupą symetrii konfiguracji Desarguesa, a podgrupa rzędu 2 zamienia role wierzchołków reprezentujących punkty konfiguracji Desarguesa i wierzchołków reprezentujących linie. Alternatywnie, jeśli chodzi o dwudzielny wykres Knesera , symetryczna grupa na pięciu punktach działa oddzielnie na dwuelementowe i trzyelementowe podzbiory pięciu punktów, a uzupełnienie podzbiorów tworzy grupę rzędu drugiego, która przekształca jeden typ podzbioru w inny. Grupa symetryczna w pięciu punktach jest również grupą symetrii grafu Petersena , a podgrupa rzędu 2 zamienia wierzchołki w każdej parze wierzchołków utworzonej w konstrukcji podwójnego pokrycia.

Uogólniony graf Petersena G ( n , k ) jest przechodni przez wierzchołki wtedy i tylko wtedy, gdy n = 10 i k = 2 lub gdy k ² ≡ ±1 (mod n ) i jest przechodni przez krawędzie tylko w następujących siedmiu przypadkach: ( n , k ) = (4, 1) , (5, 2) , (8, 3) , (10, 2) , (10, 3) , (12, 5) , (24, 5) . Tak więc wykres Desarguesa jest jednym z zaledwie siedmiu symetrycznych uogólnionych grafów Petersena. Wśród tych siedmiu grafów są graf sześcienny G (4, 1) , graf Petersena G (5, 2) , graf Möbiusa – Kantora G (8, 3) , graf dwunastościenny G (10, 2) i wykres Nauru G. (12, 5) .

Charakterystyczny wielomian wykresu Desarguesa to

${\ Displaystyle (x-3) (x-2) ^ {4} (x-1) ^ {5} (x + 1) ^ {5} (x + 2) ^ {4} (x + 3). \,}$

Dlatego wykres Desarguesa jest grafem całkowym : jego widmo składa się wyłącznie z liczb całkowitych.

Aplikacje

W chemii wykres Desarguesa jest znany jako wykres Desarguesa – Leviego ; służy do organizowania układów stereoizomerów związków 5- ligandowych . W tym zastosowaniu trzydzieści krawędzi wykresu odpowiada pseudorotacjom ligandów.

Inne właściwości

Wykres Desarguesa ma prostoliniowe przecięcie numer 6 i jest najmniejszym wykresem sześciennym z tym numerem przecięcia (sekwencja A110507 w OEIS ). Jest to jedyny znany niepłaski sześcienny sześcian częściowy .

Graf Desarguesa ma liczbę chromatyczną 2, indeks chromatyczny 3, promień 5, średnicę 5 i obwód 6. Jest to również graf Hamiltona połączony z 3 wierzchołkami i 3 krawędziami . Ma grubość książki 3 i numer kolejki 2.

wszystkie grafy regularnych odległości sześciennych . Wykres Desarguesa jest jednym z 13 takich wykresów.

Graf Desarguesa można osadzić jako podwójną regularną mapę samo- Petiego w nieorientowalnej rozmaitości rodzaju 6, z dziesięciokątnymi ścianami.

Galeria

• 

  Desargues wykres kolorowy, aby podkreślić różne cykle.

• 

  Indeks chromatyczny wykresu Desarguesa wynosi 3.

• 

  Liczba chromatyczna wykresu Desarguesa wynosi 2.