Wykres kwantowy

Ten artykuł dotyczy wykresów metrycznych wyposażonych w operator różniczkowy. Informacje o stanach kwantowych reprezentowanych przez wykresy można znaleźć w artykule Stan wykresu .

W matematyce i fizyce graf kwantowy to liniowa struktura wierzchołków połączonych krawędziami w kształcie sieci (tj. graf ) , w której każdej krawędzi przypisana jest długość i na każdej z nich nałożone jest równanie różniczkowe (lub pseudoróżniczkowe). krawędź. Przykładem może być sieć elektroenergetyczna składająca się z linii energetycznych (krawędzi) połączonych na stacjach transformatorowych (wierzchołkach); równania różniczkowe opisywałyby następnie napięcie wzdłuż każdej z linii, z warunkami brzegowymi dla każdej krawędzi podanymi na sąsiednich wierzchołkach zapewniającymi, że prąd dodany na wszystkich krawędziach sumuje się do zera w każdym wierzchołku.

Wykresy kwantowe zostały po raz pierwszy zbadane przez Linusa Paulinga jako modele swobodnych elektronów w cząsteczkach organicznych w latach trzydziestych XX wieku. Pojawiają się również w różnych kontekstach matematycznych, np. jako układy modelowe w chaosie kwantowym , w badaniu falowodów , w kryształach fotonicznych i lokalizacji Andersona lub jako ograniczenie kurczenia się cienkich drutów. Wykresy kwantowe stały się czołowymi modelami w fizyce mezoskopowej używanymi do teoretycznego zrozumienia nanotechnologii . Inną, prostszą koncepcję grafów kwantowych wprowadzili Freedman i in.

Oprócz faktycznego rozwiązywania równań różniczkowych przedstawionych na wykresie kwantowym dla celów konkretnych zastosowań, typowe pytania, które się pojawiają, to kwestie sterowalności ( jakie dane wejściowe muszą zostać dostarczone, aby doprowadzić system do pożądanego stanu, na przykład zapewnienie wystarczającej mocy dla wszystkich domów w sieci energetycznej) i identyfikowalność (jak i gdzie należy coś zmierzyć, aby uzyskać pełny obraz stanu systemu, na przykład pomiar ciśnienia w sieci wodociągowej w celu ustalenia, czy rura jest nieszczelna).

Wykresy metryczne

Wykres metryczny osadzony w płaszczyźnie z trzema otwartymi krawędziami. Linia przerywana oznacza $.$ metryczną między dwoma $i$

Wykres metryczny to wykres $, v_ {2}) \ w E}$ zbioru $v_$ i zestawu krawędzi, gdzie każda krawędź $)$${\ displaystyle e = ($${$ zostało powiązane z przedziałem, tak że ${\ displaystyle$ jest współrzędną przedziału, wierzchołek odpowiada $\$$displaystyle x_ {e} = 0}$ i v $v_ {2}}$${\ displaystyle x_ {e} = L_ {e}}$ i odwrotnie. Wybór wierzchołka leżącego na zero jest dowolny, a alternatywa odpowiada zmianie współrzędnej na krawędzi. Wykres ma naturalną metrykę: dla dwóch punktów ${\ displaystyle x, y}$ na wykresie $.$ wykresu

Grafy otwarte: w modelu grafów kombinatorycznych krawędzie zawsze łączą pary wierzchołków, natomiast w grafie kwantowym można również uwzględnić krawędzie półnieskończone. Są to krawędzie powiązane $displaystyle x_ {e} =$ przedziałem dołączonym do pojedynczego wierzchołka w punkcie $=$. A graph with one or more such open edges is referred to as an open graph.

Wykresy kwantowe

Wykresy kwantowe to wykresy metryczne wyposażone w operator różniczkowy (lub pseudoróżniczkowy) działający na funkcje na wykresie. Funkcja $wykresie metrycznym$ zdefiniowana jako $}$ -krotka funkcji w przedziałach $\ displaystyle f_ {e} (x_ {e})$ Przestrzeń Hilberta wykresu to ${\ Displaystyle \bigoplus _ {e \ in E} L ^ {2} ([0, L_ {e}])}$ gdzie iloczyn wewnętrzny dwóch funkcji wynosi

$g \ rangle = \ suma _ {e \ w E} \int _{0}^{L_{e}}f_{e}^{*}(x_{e})g_{e}(x_{e})\,dx_{e},}$

$nieskończony$ w przypadku otwartej krawędzi. Najprostszym przykładem operatora na wykresie metrycznym jest operator Laplace'a . Operator na krawędzi to ${\ Displaystyle - {\ Frac {{\textrm {d}} ^ {2}} {{\textrm {d}}x_ {e}^{2}} }}$ gdzie $krawędzi$ . Aby operator mógł się samosprzężyć, należy określić odpowiednią domenę. Zwykle osiąga się to poprzez wykorzystanie przestrzeni Sobolewa $funkcji$ na krawędziach wykresu i określenia warunków dopasowania na wierzchołkach

$,$ , jest samosprzężony Dirichleta dla każdej krawędzi. Funkcję własną na skończonej krawędzi można zapisać jako

${\ Displaystyle f_ {e} (x_ {e}) = \ sin \ lewo ({\ Frac {n \ pi x_ {e}} {L_ {e}}}\right)}$

dla liczby całkowitej $displaystyle n}$ \ Jeśli graf jest zamknięty bez nieskończonych krawędzi, a długości krawędzi wykresu są racjonalnie niezależne, wówczas funkcja własna jest obsługiwana na pojedynczej krawędzi wykresu, a wartości własne wynoszą n 2 π 2 L mi 2 $n ^{2}\pi ^{2}}{L_{e}^{2}}}}$ . Warunki Dirichleta nie pozwalają na interakcję między przedziałami, zatem widmo jest takie samo, jak widmo zbioru rozłączonych krawędzi.

Bardziej interesującymi warunkami dopasowania samosprzężonego, które umożliwiają interakcję między krawędziami, są warunki dopasowania Neumanna lub naturalne. Funkcja w dziedzinie operatora jest ciągła w każdym miejscu wykresu, a suma wychodzących pochodnych w wierzchołku wynosi zero, fa {\ $f}$

${\ Displaystyle \ suma _ {e \ sim v} f' (v) = 0 \,}$

gdzie ${\ Displaystyle f' (v) = f' (0)}$ jeśli wierzchołek znajduje $displaystyle x = 0}$ w $\$ i $f' (v) = -f' (L_ {e})}$$jeśli$ jest na ${\ displaystyle x = L_ {e}$ }

Zbadano także właściwości innych operatorów na wykresach metrycznych.

• Należą do nich bardziej ogólna klasa operatorów Schrödingera,

${\ displaystyle \ lewo (ja {\ frac {\textrm {d}} {{\textrm {d}}x_{e}}}+A_{e}(x_{e})\right)^{2}+V_{e}(x_{e})\ ,}$

gdzie $wektora magnetycznego$$„$ na krawędzi i potencjałem skalarnym.

• Innym przykładem jest operator Diraca na wykresie, który jest operatorem o wartościach macierzowych, działającym na funkcje o wartościach wektorowych, które opisują mechanikę kwantową cząstek o wewnętrznym momencie pędu równym połowie, takich jak elektron .
• Operator Dirichleta-Neumanna na wykresie jest operatorem pseudoróżniczkowym powstającym podczas badania kryształów fotonicznych .

Twierdzenia

Wszystkie warunki samosprzężonego dopasowania operatora Laplace'a na wykresie można klasyfikować według schematu Kostrykina i Schradera. W praktyce często wygodniej jest przyjąć formalizm wprowadzony przez Kuchmenta, patrz, który automatycznie daje operator w postaci wariacyjnej.

Niech będzie wierzchołkiem, $z$$krawędzie$ . Dla uproszczenia wybieramy współrzędne na krawędziach tak, aby leżały w punkcie $dla$${\ displaystyle x_ {e} = 0}$ każdego spotkania krawędzi w ${\ displaystyle v}$ . Dla funkcji na $wykresie$

${\ Displaystyle \ mathbf {f} = (f_ {e_ {1}} (0), f_ {e_ {2}} (0), \ kropki, f_ {e_ {d}} (0)) ^ {T} ,\qquad \mathbf {f} '=(f'_{e_{1}}(0),f'_{e_{2}}(0),\dots ,f'_{e_{d}}( 0))^{T}.}$

$Warunki$ dopasowania w $}$ określić za pomocą pary macierzy i za pomocą równania liniowego, ${\ displaystyle$

${\ Displaystyle A \ mathbf {f} + B \ mathbf {f} '= \ mathbf {0}.}$

${\ Displaystyle AB ^ {*} = BA ^ {*}.}$$,$ samosprzężony maksymalną $∗$ i

Widmo operatora Laplace'a na skończonym wykresie można wygodnie opisać za pomocą podejścia opartego na macierzy rozpraszania wprowadzonego przez Kottosa i Smilansky'ego. Problem wartości własnej na krawędzi jest następujący:

${\ Displaystyle - {\ Frac {d ^ {2}} {dx_ {e} ^ {2}}} f_ {e} (x_ {e}) = k ^ {2} f_ {e} (x_ {e} ).\,}$

Zatem rozwiązanie na krawędzi można zapisać jako liniową kombinację fal płaskich .

${\ Displaystyle f_ {e} (x_ {e}) = c_ {e}} }^{-ikx_{e}}.\,}$

$}$ zależnym od czasu równaniu Schrödingera $wychodzącej$ fali płaskiej w $i$ współczynnikiem przychodzącej fali płaskiej w {\ $displaystyle 0$$\displaystyle 0}$ . Warunki dopasowania w $macierz$ rozpraszania

${\ Displaystyle S (k) = - (A + ikB) ^ {- 1} (A-ikB). \,}$

Macierz rozpraszania wiąże wektory współczynników przychodzącej i wychodzącej fali płaskiej w $\$ do $displaystyle \ mathbf {c} = S (k) {\ kapelusz {\ mathbf { c} }}}$ . W przypadku $jest$ dopasowania samosprzężonego unitarny. Element ${\ Displaystyle \ sigma _ {(uv) (vw)}}$$\ displaystyle S}$ { $\ displaystyle ($ od skierowanej krawędzi $} Jednak dla dużej klasy warunków$ , ogólnie zależy od $uv$ { $dopasowania$ macierz S jest niezależna . Na przykład z warunkami dopasowania Neumanna

${\ Displaystyle A = \ lewo ({\ początek {tablica}} ccccc} 1 i - 1 i 0 i 0 i \ kropki \\ 0 i 1 i - 1 i 0 i \ kropki \\ i & \ ddots i \ ddots & \\ 0 i \ kropki & 0 i 1 i -1 \\ 0 i \ kropki &0&0&0\\\end{array}}\right),\quad B=\left({\begin{array}{cccc}0&0&\dots &0\\\vdots &\vdots &&\vdots \\0&0&\dots &0 \\1&1&\kropki &1\\\end{array}}\right).}$

Podstawienie w równaniu daje $}$ amplitudy przejścia ${\ displaystyle S$

${\ Displaystyle \ sigma _ {(uv) (vw)} = {\ Frac {2} {d}} - \ delta _ {uw}. \,}$

gdzie $,$ funkcją delta Kroneckera, która wynosi jeden $jeśli$ przeciwnym Z amplitud przejść możemy zdefiniować ${\ Displaystyle 2 | E | \ razy 2 | E |}$ matryca

${\ Displaystyle U _ {(uv) (lm)} (k) = \ delta _ {vl} \ sigma _ {(uv) (vm)} (k) {\textrm {e}} ^ {ikL_ {(uv) }}.\,}$

$ją$ traktować jako operator ewolucji kwantowej na wykresie. Jest unitarny i działa na wektorze $($ współczynniki fali płaskiej na wykresie, gdzie jest współczynnikiem fali płaskiej przemieszczającej się od do $\ displaystyle c_ {(uv)}}$ do $styl wyświetlania v}$$\ u {$$displaystyle u}$ . Faza ${\ Displaystyle {\ textrm {e}} ^ {ikL_ {(uv)}}}$ to faza uzyskiwana przez falę płaską podczas propagacji od wierzchołka do wierzchołka ${\ displaystyle u}$${\ displaystyle v}$ .

Warunek kwantyzacji: Funkcję własną na wykresie można zdefiniować poprzez skojarzone z nią $współczynniki$ fali płaskiej. Ponieważ funkcja własna jest stacjonarna w procesie ewolucji kwantowej, warunek kwantyzacji dla wykresu można zapisać za pomocą operatora ewolucji.

${\ Displaystyle | U (k) -I | = 0. \,}$

$macierz$ własne $_$ wartościach $gdzie$ ma _ Uporządkujemy widmo za pomocą ${\ displaystyle 0 \ leqslant k_ {0} \ leqslant k_ {1} \ leqslant \ dots}$ .

Pierwszy wzór śladowy dla wykresu wyprowadził Roth (1983). W 1997 $.$ i Smilansky wykorzystali powyższy warunek kwantyzacji, aby otrzymać następujący wzór śladu dla operatora Laplace'a na wykresie, gdy amplitudy przejść są niezależne od Wzór śladu łączy widmo z okresowymi orbitami na wykresie.

${\ Displaystyle d (k): = \ suma _ {j = 0} ^ {\ infty} \ delta (kk_ {j}) = {\ Frac {L} {\ pi}} + {\ Frac {1 }$

${\ displaystyle d (k)}$ nazywa się gęstością stanów. Prawa strona wzoru śladu składa się z dwóch członów, termin Weyla $jest$ jest sumą wszystkich na wykresie ${\ displaystyle p = (e_ {1}, e_ {2}, \ kropki, e_ {n})}$${\ Displaystyle L_ {p} = \ suma _ {e \ w p} L_ {e}}$ to długość orbity i ${\ displaystyle L = \ suma _{e\in E}L_{e}}$ to całkowita długość wykresu. $zlicza$ przypadku orbity utworzonej przez powtórzenie krótszej prymitywnej orbity liczbę ponownych podziałów. ${\ Displaystyle A_ {p} = \ sigma _ {e_ {1} e_ {2}} \ sigma _ {e_ {2} e_ {3}} \ kropki \ sigma _ {e_ {n}e_{1}}}$ jest iloczynem amplitud przejść w wierzchołkach wykresu wokół orbity.

Aplikacje

Cząsteczka naftalenu

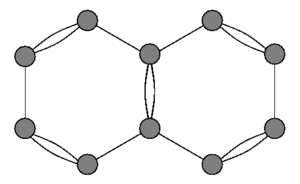
Wykresy kwantowe po raz pierwszy zastosowano w latach trzydziestych XX wieku do modelowania widma wolnych elektronów w cząsteczkach organicznych, takich jak naftalen , patrz rysunek. W pierwszym przybliżeniu przyjmuje się, że atomy są wierzchołkami, podczas gdy elektrony σ tworzą wiązania, które ustalają ramę w kształcie cząsteczki, w której ograniczone są wolne elektrony.

Podobny problem pojawia się przy rozważaniu falowodów kwantowych. Są to układy mezoskopowe – systemy zbudowane o szerokości w skali nanometrów. Falowód kwantowy można traktować jako pogrubiony wykres, którego krawędzie są cienkimi rurkami. Widmo operatora Laplace'a w tej dziedzinie zbiega się z widmem operatora Laplace'a na wykresie pod pewnymi warunkami. Zrozumienie systemów mezoskopowych odgrywa ważną rolę w dziedzinie nanotechnologii .

W 1997 Kottos i Smilansky zaproponowali grafy kwantowe jako model do badania chaosu kwantowego , mechaniki kwantowej układów klasycznie chaotycznych. Klasyczny $ruch$ na wykresie można zdefiniować jako probabilistyczny łańcuch Markowa , w którym prawdopodobieństwo rozproszenia od krawędzi krawędzi $kwadratu$ amplitudy przejścia kwantowego, ${\ displaystyle | \ sigma _ {ef} | ^ {2}}$ . Dla prawie wszystkich skończonych spójnych grafów kwantowych dynamika probabilistyczna jest ergodyczna i mieszana, innymi słowy chaotyczna.

W badaniu kryształów fotonicznych pojawiają się wykresy kwantowe osadzone w dwóch lub trzech wymiarach . W dwóch wymiarach prosty model kryształu fotonicznego składa się z wielokątnych komórek gęstego dielektryka z wąskimi granicami między komórkami wypełnionymi powietrzem. Badanie modów dielektrycznych, które pozostają głównie w dielektryku, prowadzi do powstania operatora pseudoróżniczkowego na wykresie podążającym za wąskimi granicami międzyfazowymi.

Okresowe wykresy kwantowe, takie jak sieć w, są powszechnymi modelami układów okresowych, a wykresy kwantowe zostały zastosowane do badania zjawisk lokalizacji Andersona , gdzie zlokalizowane stany występują w ${\ displaystyle {\ mathbb {R}} ^ {2}}$ krawędź pasm widmowych w obecności zaburzenia.

Zobacz też

• Drabina Schilda , powieść traktująca o fikcyjnej teorii grafów kwantowych
• Diagram Feynmana