Efekt Eötvösa

Aby zapoznać się z eksperymentem mającym na celu sprawdzenie równości masy grawitacyjnej i bezwładnej, zobacz eksperyment Eötvösa .

Efekt Eötvösa to zmiana mierzonej grawitacji Ziemi spowodowana zmianą przyspieszenia odśrodkowego wynikającą z prędkości w kierunku wschodnim lub zachodnim . Podczas ruchu na wschód prędkość kątowa obiektu wzrasta (oprócz obrotu Ziemi ), a zatem siła odśrodkowa również wzrasta, powodując odczuwalne zmniejszenie siły grawitacji.

Odkrycie

Na początku XX wieku niemiecki zespół z Instytutu Geodezyjnego w Poczdamie przeprowadził pomiary grawitacji na statkach poruszających się po Oceanie Atlantyckim , Indyjskim i Pacyfiku . Badając ich wyniki, węgierski szlachcic i fizyk Baron Roland von Eötvös ( Loránd Eötvös ) zauważył, że odczyty były niższe, gdy łódź poruszała się na wschód, a wyższe, gdy poruszała się na zachód. Zidentyfikował to przede wszystkim jako konsekwencję obrotu Ziemi. W 1908 roku dokonano nowych pomiarów na Morzu Czarnym na dwóch statkach, jednym poruszającym się na wschód, a drugim na zachód. Wyniki potwierdziły twierdzenie Eötvösa.

Sformułowanie

Geodeci używają następującego wzoru, aby skorygować prędkość względem Ziemi podczas biegu grawimetrycznego .

${\ Displaystyle a_ {r} = 2 \ Omega u \ cos \ phi + {\ Frac {u ^ {2} + v ^ {2}} {R}}.}$

Tutaj,

${r}}$ to przyspieszenie względne

${ \ displaystyle$ Ziemi

$to prędkość$ to prędkość w kierunku wzdłużnym (wschód-zachód)

${\ displaystyle \ phi }$ to szerokość geograficzna, na której wykonywane są pomiary.

${\ displaystyle v}$ to prędkość w kierunku równoleżnikowym (północ-południe)

${\ displaystyle R}$ to promień Ziemi

Pierwszy wyraz we wzorze, 2 Ωu cos( ϕ ), odpowiada efektowi Eötvösa. Drugi człon to udoskonalenie, które w normalnych warunkach jest znacznie mniejsze niż efekt Eötvösa.

Wyjaśnienie fizyczne

Najpopularniejszym projektem grawimetru do prac terenowych jest konstrukcja sprężynowa; sprężyna podtrzymująca wewnętrzny ciężarek. Siła zawieszenia zapewniana przez sprężynę przeciwdziała sile grawitacji. Dobrze wykonana sprężyna ma tę właściwość, że siła wywierana przez sprężynę jest proporcjonalna do wydłużenia sprężyny z jej położenia równowagi ( prawo Hooke'a ). Im silniejsza efektywna grawitacja w określonym miejscu, tym bardziej rozciąga się sprężyna; sprężyna rozciąga się na długość, na której utrzymywany jest ciężar wewnętrzny. Ponadto ruchome części grawimetru zostaną wytłumione, aby był mniej podatny na wpływy zewnętrzne, takie jak wibracje.

Do obliczeń przyjęto, że odważnik wewnętrzny ma masę dziesięciu kilogramów (10 kg; 10 000 g). Przyjmuje się, że do pomiarów wykorzystuje się środek transportu, który zapewnia dobrą prędkość przy bardzo płynnym poruszaniu się: sterowiec. Niech prędkość przelotowa sterowca wynosi 25 metrów na sekundę (90 km/h; 56 mil/h).

Ruch wzdłuż równika

Wykres siły działającej na 10-kilogramowy obiekt w funkcji jego prędkości poruszającej się wzdłuż równika Ziemi (mierzonej w obracającej się ramie). (Dodatnia siła na wykresie jest skierowana w górę. Dodatnia prędkość jest skierowana na wschód, a ujemna prędkość jest skierowana na zachód).

Aby obliczyć, ile potrzeba, aby ciężar wewnętrzny grawimetru był zawieszony w neutralnym położeniu, gdy jest on nieruchomy względem Ziemi, należy wziąć pod uwagę obrót Ziemi. Na równiku prędkość powierzchni Ziemi wynosi około 465 metrów na sekundę (1674 km / h; 1040 mil / h). Wielkość siły dośrodkowej wymaganej do spowodowania ruchu obiektu po torze kołowym o promieniu 6378 km (promień równikowy Ziemi) z prędkością 465 m/s wynosi około 0,034 niutona na kilogram masy. W przypadku wagi wewnętrznej 10 000 gramów odpowiada to około 0,34 niutona. Wymagana siła zawieszenia to masa wewnętrznego ciężarka (pomnożona przez przyspieszenie grawitacyjne) minus te 0,34 niutona. Innymi słowy: każdy obiekt obracający się wspólnie z Ziemią na równiku ma zmierzoną wagę zmniejszoną o 0,34 procent dzięki obrotowi Ziemi.

Podczas lotu z prędkością 10 m/s na wschód, całkowita prędkość wynosi 465 + 10 = 475 m/s, co wymaga siły dośrodkowej około 0,0354 niutona na kilogram. Płynąc z prędkością 10 m/s na zachód, prędkość netto wynosi 465 - 10 = 455 m/s, co wymaga około 0,0325 niutona na kilogram. Jeśli więc wewnętrzny ciężarek jest zawieszony neutralnie podczas lotu na wschód, po odwróceniu kursu nie będzie już zawieszony neutralnie: pozorna masa wewnętrznego ciężarka o masie 10 000 gramów wzrośnie o około 3 gramy, a sprężyna grawimetru musi się wydłużyć trochę więcej, aby pomieścić ten większy ciężar.

W wysokowydajnych modelach meteorologicznych efekt ten należy uwzględnić w skali ziemskiej. Masy powietrza o znacznej prędkości względem Ziemi mają tendencję do przemieszczania się na inną wysokość , co należy wziąć pod uwagę, gdy wymagania dotyczące dokładności są surowe.

Wyprowadzenie wzoru na przypadek uproszczony

Wyprowadzenie wzoru na ruch wzdłuż równika.

Wygodnym układem współrzędnych w tej sytuacji jest bezwładnościowy układ współrzędnych, który porusza się wraz ze środkiem masy Ziemi. Wtedy obowiązuje następująca zasada: obiekty spoczywające na powierzchni Ziemi, obracające się wspólnie z Ziemią, krążą wokół osi Ziemi, a więc mają przyspieszenie dośrodkowe względem tego bezwładnościowego układu współrzędnych.

Poszukiwana jest różnica w przyspieszeniu dośrodkowym sterowca pomiarowego pomiędzy stacją nieruchomą względem Ziemi a prędkością względem Ziemi. Poniższe wyprowadzenie dotyczy wyłącznie ruchu w kierunku wschód-zachód lub zachód-wschód.

Notacja:

${\ displaystyle a_ {u}}$ to całkowite przyspieszenie dośrodkowe podczas ruchu po powierzchni Ziemi.

$\ displaystyle a_ {s}}$ jest przyspieszeniem dośrodkowym podczas postoju względem Ziemi.

${\ Displaystyle \ Omega}$ to prędkość kątowa Ziemi: jeden obrót na gwiezdny dzień .

$jest prędkością kątową sterowca względem$ Ziemi.

${\ Displaystyle \ lewo (\ Omega + \ omega _ {r} \ prawej)}$ to całkowita prędkość kątowa sterowca.

${\ Displaystyle u = \ omega _ {r} R}$ to prędkość sterowca (prędkość względem Ziemi).

${\ displaystyle R}$ to promień Ziemi.

${\ Displaystyle {\ rozpocząć {wyrównane} a_ {r} & = a_ {u} -a_ {s} \\& = \ lewo (\ omega + \ omega _ {r} \ w prawo)^{2}R-\Omega ^{2}R\\&=\Omega ^{2}R+2\Omega \omega _{r}R+\omega _{r}^{2}R-\ Omega ^{2}R\\&=2\Omega \omega _{r}R+\omega _{r}^{2}R\\&=2\Omega u+{\frac {u^{2}}{ R}}\\\koniec {wyrównany}}}$

Można łatwo zauważyć, że powyższy wzór na ruch wzdłuż równika wynika z bardziej ogólnego równania poniżej dla dowolnej szerokości geograficznej, gdzie wzdłuż równika v = 0,0 i sałata $\ Displaystyle \ cos \ phi = 1,0}$

${\ Displaystyle a_ {r} = 2 \ Omega u \ cos \ phi + {\ Frac {u ^ {2} + v ^ {2}} { R}}}$

Drugi człon reprezentuje wymagane przyspieszenie dośrodkowe , aby sterowiec podążał za krzywizną ziemi. Jest niezależny zarówno od obrotu Ziemi, jak i kierunku ruchu. Na przykład, gdy samolot z przyrządami do odczytu grawimetrycznego przelatuje nad jednym z biegunów na stałej wysokości, trajektoria samolotu podąża za krzywizną ziemi. Pierwszy człon we wzorze wynosi wtedy zero, ponieważ cosinus kąta wynosi zero, a drugi człon oznacza wówczas przyspieszenie dośrodkowe podążające za krzywizną powierzchni Ziemi.

Wyjaśnienie cosinusa w pierwszym wyrazie

Siła grawitacji i siła normalna . Wypadkowa siła działa jak wymagana siła dośrodkowa.

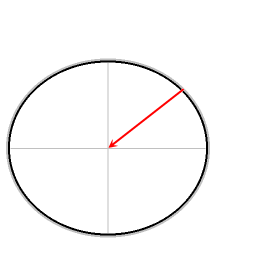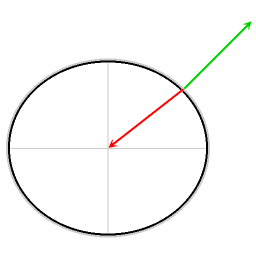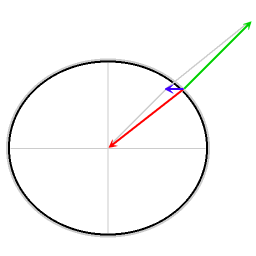
Matematyczne wyprowadzenie efektu Eötvösa dla ruchu wzdłuż równika wyjaśnia współczynnik 2 w pierwszym wyrazie wzoru na poprawkę Eötvösa. To, co pozostaje do wyjaśnienia, to współczynnik cosinusowy.

Ze względu na swój obrót Ziemia nie ma kulistego kształtu, występuje wybrzuszenie równikowe . Siła grawitacji skierowana jest w stronę środka Ziemi. Siła normalna jest prostopadła do powierzchni lokalnej.

Na biegunach i na równiku siła grawitacji i siła normalna mają dokładnie przeciwny kierunek. Na każdej innej szerokości geograficznej te dwie szerokości nie są dokładnie przeciwne, więc istnieje siła wypadkowa, która działa w kierunku osi Ziemi. Na każdej szerokości geograficznej istnieje dokładnie taka wielkość siły dośrodkowej, która jest niezbędna do utrzymania równej grubości warstwy atmosfery. (Stała Ziemia jest plastyczna. Ilekroć kształt stałej Ziemi nie jest całkowicie w równowadze z jej prędkością rotacji, wówczas naprężenie ścinające odkształca stałą Ziemię przez miliony lat, aż naprężenie ścinające zostanie rozwiązane.)

Znowu przykład sterowca jest wygodny do omówienia działających sił. Kiedy sterowiec ma prędkość względem Ziemi w kierunku równoleżnikowym, wówczas ciężar sterowca nie jest taki sam, jak wtedy, gdy sterowiec jest nieruchomy względem Ziemi.

Jeśli sterowiec porusza się z prędkością na wschód, to w pewnym sensie „rozpędza się”. Sytuację można porównać do samochodu wyścigowego na torze z nachyleniem i wyjątkowo śliską nawierzchnią. Jeśli samochód wyścigowy jedzie zbyt szybko, samochód będzie dryfował szeroko. Dla sterowca w locie oznacza to zmniejszenie masy w porównaniu do masy w stanie spoczynku względem Ziemi.

Jeśli sterowiec ma prędkość w kierunku zachodnim, sytuacja przypomina sytuację samochodu wyścigowego na przechylonym torze, jadącego zbyt wolno: na śliskiej nawierzchni samochód opadnie. Dla sterowca oznacza to zwiększenie masy.

Pierwszy człon efektu Eötvösa jest proporcjonalny do składowej wymaganej siły dośrodkowej prostopadłej do lokalnej powierzchni Ziemi, a zatem jest opisany prawem cosinusa: im bliżej równika, tym silniejszy efekt.

Ruch wzdłuż 60 stopni szerokości geograficznej

Efekt Eötvösa dla obiektu poruszającego się na wschód wzdłuż 60 stopni szerokości geograficznej. Obiekt ma tendencję do oddalania się od osi Ziemi.

Efekt Eötvösa dla obiektu poruszającego się na zachód wzdłuż 60 stopni szerokości geograficznej. Obiekt ma tendencję do przyciągania w kierunku osi Ziemi.

Ten sam grawimetr jest używany ponownie, jego wewnętrzny ciężar ma masę 10 000 gramów.

Obliczanie redukcji ciężaru w stanie spoczynku względem Ziemi: Obiekt znajdujący się na 60 stopniach szerokości geograficznej, poruszający się wraz z Ziemią, porusza się po trajektorii kołowej o promieniu około 3190 km i prędkości około 233 m/s . Ta kołowa trajektoria wymaga siły dośrodkowej około 0,017 niutona na każdy kilogram masy; 0,17 niutona dla wagi wewnętrznej 10 000 gramów. Na 60 stopniach szerokości geograficznej składowa prostopadła do lokalnej powierzchni (lokalnego pionu) stanowi połowę całkowitej siły. Dlatego na 60 stopniach szerokości geograficznej każdy obiekt poruszający się razem z Ziemią ma mniejszą wagę o około 0,08 procent dzięki obrotowi Ziemi.

Obliczanie efektu Eötvösa: Gdy sterowiec leci z prędkością 25 m/s w kierunku wschodnim, całkowita prędkość wynosi 233 + 25 = 258 m/s, co wymaga siły dośrodkowej około 0,208 niutona; lokalna składowa pionowa około 0,104 niutona. Płynąc z prędkością 25 m/s w kierunku zachodnim, całkowita prędkość wynosi 233 - 25 = 208 m/s, co wymaga siły dośrodkowej około 0,135 niutona; lokalna składowa pionowa około 0,068 niutona. Stąd na 60 stopniach szerokości geograficznej różnica przed i po zawróceniu 10 000-gramowego ciężaru wewnętrznego jest różnicą 4 gramów w zmierzonej masie. (Potocznie mówi się, że ciężar jest siłą mierzoną w niutonach, a nie w gramach).

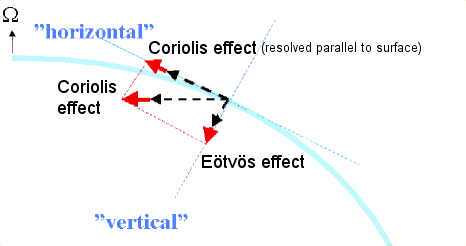
Diagramy pokazują również składową w kierunku równoległym do powierzchni lokalnej. W meteorologii i oceanografii zwyczajowo nazywa się efekt Coriolisa wpływem składnika równoległego do lokalnej powierzchni .

• Plik PDF z efektem Coriolisa . 870 KB 17 stron. Ogólna dyskusja meteorologa Andersa Perssona na temat różnych aspektów geofizyki, obejmująca efekt Coriolisa uwzględniany w meteorologii i oceanografii, efekt Eötvösa, wahadło Foucaulta i kolumny Taylora.

Linki zewnętrzne

• W 1915 roku Eötvös skonstruował urządzenie stołowe , które demonstruje efekt Eötvösa. Urządzenie znajduje się wśród innych instrumentów wystawionych w małym muzeum poświęconym twórczości i życiu Eötvösa.
• Większe zdjęcie urządzenia stołowego ze strony internetowej muzeum.