Funkcja Mittaga-Lefflera

Funkcji Mittaga-Lefflera można użyć do ciągłej interpolacji między funkcją Gaussa i Lorentza.

W matematyce funkcja Mittaga -Lefflera $\ displaystyle$ funkcją $\beta}$ , złożoną funkcją , $}$ zależy od dwóch parametrów zespolonych β $alpha$ . Można to zdefiniować za pomocą następującego szeregu , gdy część rzeczywista jest ściśle dodatnia: ${\ displaystyle \ alpha}$

{\ Displaystyle E _ {\ alfa, \ beta} (z) = \ suma _ {k = 0} ^ {\ infty} {\frac {z^{k}}{\Gamma (\alpha k+\beta)}},}

gdzie $_$ _ _ _ mi $)$ ${\ Displaystyle E _ {\ alfa} (z) = E _ {$ mi . Dla , powyższy szereg jest równy rozwinięciu Taylora szeregu geometrycznego iw konsekwencji ${\ displaystyle \ alpha = 0}$ ${\ Displaystyle E_ {0, \ beta} (z) = {\ Frac {1} {\ Gamma (\ beta)}} {\ Frac {1 }{1-z}}}$ .

$są$ przypadku , gdy $rzeczywiste$ i $dodatnie$ , szereg jest zbieżny dla wszystkich wartości argumentu więc funkcja Mittaga-Lefflera jest całą funkcją . Ta funkcja nosi imię Gösty Mittaga-Lefflera . Ta klasa funkcji jest ważna w teorii rachunku ułamkowego .

Dla ${\ Displaystyle \ alpha > 0}$ $Displaystyle E _ {\$ Mittaga-Lefflera jest funkcją rzędu mi $}$ i jest w pewnym sensie najprostszą całą funkcją swojego rzędu.

Funkcja Mittaga-Lefflera spełnia właściwość powtarzalności (Twierdzenie 5.1 z )

{\ Displaystyle E _ {\ alfa, \ beta} (z) = {\ Frac {1} {z}}E_{\alpha ,\beta -\alpha}(z)-{\frac {1}{z\Gamma (\beta -\alpha)}},}

skąd asymptotyczna ekspansja Poincarégo

{\ Displaystyle E _ {\ alfa, \ beta} (z) \ sim - \ suma _ {k = 1} {\ frac {1}{z^{k}\Gamma (\beta -k\alpha )}}}

wynika, co jest prawdziwe dla ${\ Displaystyle z \ do - \ infty}$ .

Przypadki specjalne

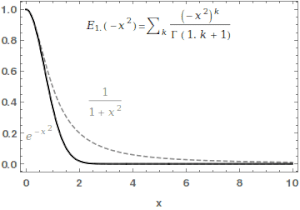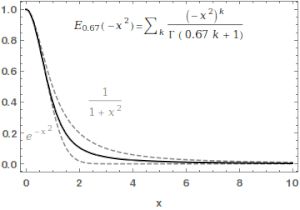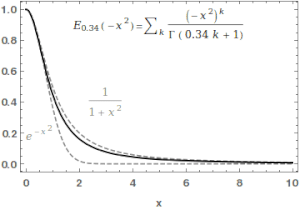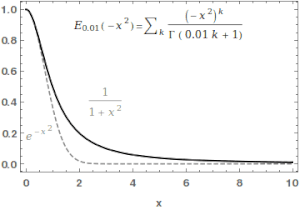
Dla ${\ Displaystyle \ alpha = 0,1/2,1,2}$ znajdujemy: (Sekcja 2)

Funkcja błędu :

{\ Displaystyle E _ {\ Frac {1} {2}} (z) = \ exp (z ^ {2}) \ operatorname {erfc} (-z).}

Suma postępu geometrycznego :

{\ Displaystyle E_ {0} (z) = \ suma _ {k = 0} ^ {\ infty} z ^ {k} = {\ Frac {1} {1-z}}, \, | z |<1.}

Funkcja wykładnicza :

{\ Displaystyle E_ {1} (z) = \ suma _ {k = 0} ^ {\ infty} {\ Frac {z ^ {k}} {\ Gamma (k + 1)}} = \ suma _ {k =0}^{\infty}{\frac {z^{k}}{k!}}=\exp(z).}

Cosinus hiperboliczny :

{\ Displaystyle E_ {2} (z) = \ cosh ({\ sqrt {z}}), {\ tekst {i}} E_ {2} (- z ^ {2}) = \ cos (z).}

Dla ${\ displaystyle \ beta = 2}$ mamy

{\ Displaystyle E_ {1,2} (z) = {\ Frac {e ^ {z} -1} {z}},}

{\ Displaystyle E_ {2,2} (z) = {\ Frac {\ sinh ({\ sqrt {z}})} {\ sqrt {z}}}.}

Dla całki ${\ Displaystyle \ alpha = 0,1,2}$

{\ Displaystyle \ int _ {0} ^ {z} E _ {\ alfa} (-s ^ {2}) \ {\ operatorname {d}} s}

daje odpowiednio: ${\ Displaystyle \ arctan (z)}$ , ${\ Displaystyle {\ tfrac {\ sqrt {\ pi}} {2}} \ operatorname {erf} ( z)}$ , ${\ Displaystyle \ sin (z)}$ .

Całkowa reprezentacja Mittaga-Lefflera

Całkową reprezentacją funkcji Mittaga-Lefflera jest (Sekcja 6 z )

{\ Displaystyle E _ {\ alfa, \ beta} (z)={\frac {1}{2\pi i}}\oint _{C}{\frac {t^{\alpha -\beta}e^{t}}{t^{\alpha}- z}}\,dt,\Re (\alpha )>0,\Re (\beta)>0,}

gdzie kontur zaczyna się i kończy w ${\ displaystyle - \ infty} i krąży$ $wokół osobliwości i$ rozgałęzień całki.

Powiązane z transformatą Laplace'a i sumowaniem Mittaga-Lefflera jest wyrażenie (równanie (7,5) z ) ${\ displaystyle m = 0$ }

{\ Displaystyle \ int _ {0} ^ {\ infty} e ^ {-tz} t ^ {\ beta -1} E _ {\ alfa, \ beta} (\ pm r \, t ^ {\ alfa}) \ ,dt={\frac {z^{\alpha -\beta}}{z^{\alpha}\mp r}},\Re (z)>0,\Re (\alpha)>0,\Re ( \beta )>0.}

Zastosowania funkcji Mittaga-Lefflera

Jednym z zastosowań funkcji Mittaga-Lefflera jest modelowanie materiałów lepkosprężystych ułamkowego rzędu. Eksperymentalne badania nad zależnym od czasu zachowaniem relaksacyjnym materiałów lepkosprężystych charakteryzują się bardzo szybkim spadkiem naprężenia na początku procesu relaksacji i bardzo powolnym zanikiem przez długi czas. Osiągnięcie stałej wartości asymptotycznej może zająć nawet dużo czasu. Dlatego potrzeba wielu elementów Maxwella, aby opisać zachowanie relaksacyjne z wystarczającą dokładnością. Kończy się to trudnym problemem optymalizacyjnym w celu identyfikacji dużej liczby parametrów materiałowych. Z drugiej strony, z biegiem lat do teorii wprowadzono pojęcie pochodnych ułamkowych lepkosprężystość . Spośród tych modeli ułamkowy model Zenera okazał się bardzo skuteczny w przewidywaniu dynamicznej natury materiałów gumopodobnych przy niewielkiej liczbie parametrów materiałowych. Rozwiązanie odpowiedniego równania konstytutywnego prowadzi do funkcji relaksacyjnej typu Mittaga-Lefflera. Jest ona zdefiniowana przez szereg potęgowy z ujemnymi argumentami. Funkcja ta reprezentuje wszystkie istotne właściwości procesu relaksacji pod wpływem dowolnego i ciągłego sygnału ze skokiem w punkcie początkowym.

Zobacz też

Notatki

Pakiet R „MittagLeffleR” autorstwa Gurtka Gilla, Petera Straki. Implementuje funkcję Mittaga-Lefflera, dystrybucję, generowanie zmiennych losowych i estymację.

Mittag-Leffler, MG: Sur la nouvelle fonction E(x). CR Acad. nauka Paryż 137, 554–558 (1903)
Mittag-Leffler, MG: Sopra la funzione E˛.x/. Rozdzierać. R. Ak. Lincei (ser. 5) 13, 3–5 (1904)
Gorenflo R., Kilbas AA, Mainardi F., Rogosin SV, funkcje Mittaga-Lefflera, tematy pokrewne i zastosowania (Springer, Nowy Jork, 2014) 443 strony ISBN 978-3-662-43929-6
Igora Podłubnego (1998). "rozdział 1". Ułamkowe równania różniczkowe. Wprowadzenie do pochodnych ułamkowych, równań różniczkowych ułamkowych, niektórych metod ich rozwiązywania i niektórych zastosowań . Matematyka w nauce i inżynierii . Prasa akademicka. ISBN 0-12-558840-2 .
Kaia Diethelma (2010). "Rozdział 4". Analiza ułamkowych równań różniczkowych: wykład zorientowany na zastosowanie z wykorzystaniem operatorów różniczkowych typu Caputo . Notatki z wykładów z matematyki. Heidelberg i Nowy Jork: Springer-Verlag. ISBN 978-3-642-14573-5 .

Linki zewnętrzne

Ten artykuł zawiera materiał z funkcji Mittaga-Lefflera w serwisie PlanetMath , który jest objęty licencją Creative Commons Attribution/Share-Alike License .