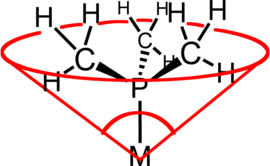
Kąt stożka ligandu
W chemii koordynacyjnej kąt stożka ligandu (typowym przykładem jest kąt stożka Tolmana lub θ ) jest miarą objętości sterycznej ligandu w kompleksie koordynacyjnym metalu przejściowego . Jest zdefiniowany jako kąt bryłowy utworzony z metalem na wierzchołku i najbardziej zewnętrznej krawędzi sfer van der Waalsa atomów liganda na obwodzie stożka (patrz rysunek). Ligandy trzeciorzędowych fosfin są powszechnie klasyfikowane przy użyciu tego parametru, ale metodę można zastosować do dowolnego ligandu. Termin kąt stożka został po raz pierwszy wprowadzony przez Chadwicka A. Tolmana , chemika prowadzącego badania w firmie DuPont . Tolman pierwotnie opracował metodę ligandów fosfinowych w kompleksach niklu, określając je na podstawie pomiarów dokładnych modeli fizycznych.
Obudowy asymetryczne
Pojęcie kąta stożka najłatwiej zobrazować za pomocą ligandów symetrycznych, np. PR 3 . Ale podejście zostało udoskonalone, aby uwzględnić mniej symetryczne ligandy typu PRR′R″, a także difosfiny. W takich asymetrycznych przypadkach, kąty połówkowe podstawników, θ i / 2 , są uśredniane, a następnie podwajane, aby znaleźć całkowity kąt stożka, θ . W przypadku difosfin θ i / 2 szkieletu jest w przybliżeniu równe połowie kąta zgryzu chelatu , zakładając kąt zgryzu 74 °, 85 ° i 90 ° dla difosfin o odpowiednio metylenowym, etylenowym i propylenowym szkielecie. Kąt stożka Manza jest często łatwiejszy do obliczenia niż kąt stożka Tolmana:
| Ligand | Kąt (°) |
|---|---|
| pH 3 | 87 |
| PF 3 | 104 |
| P(OCH 3 ) 3 | 107 |
| dmpe | 107 |
| dep | 115 |
| P( CH3 ) 3 | 118 |
| dppm | 121 |
| dppe | 125 |
| dppp | 127 |
| P ( CH2CH3 ) 3 _ | 132 |
| dcpe | 142 |
| P ( C6H5 ) 3 _ | 145 |
| ( cyklo - C6H11 ) 3 | 179 |
| P( t -Bu) 3 | 182 |
| P(C 6 F 5 ) 3 | 184 |
| P ( C6H4-2 - CH3 ) 3 _ | 194 |
| P(2,4,6- Me 3 C 6 H 2 ) 3 | 212 |
Wariacje
Metoda kąta stożka Tolmana zakłada dane empiryczne dotyczące wiązań i definiuje obwód jako maksymalny możliwy obwód wyidealizowanego swobodnie obracającego się podstawnika. Długość wiązania metal-ligand w modelu Tolmana została wyznaczona empirycznie na podstawie struktur krystalicznych tetraedrycznych kompleksów niklu. W przeciwieństwie do tego, koncepcja kąta bryłowego wywodzi zarówno długość wiązania, jak i obwód z empirycznych struktur kryształów w stanie stałym. Każdy system ma zalety.
Jeśli znana jest geometria ligandu, za pomocą krystalografii lub obliczeń, można obliczyć dokładny kąt stożka ( θ ). Nie przyjmuje się żadnych założeń dotyczących geometrii, w przeciwieństwie do metody Tolmana.
Aplikacja
Pojęcie kąta stożka ma praktyczne znaczenie w katalizie homogenicznej , ponieważ wielkość ligandu wpływa na reaktywność przyłączonego metalowego środka. Na przykład na selektywność hydroformylowania duży wpływ ma wielkość koligandów. Pomimo tego, że są jednowartościowe , niektóre fosfiny są wystarczająco duże, aby zajmować ponad połowę sfery koordynacyjnej metalowego centrum. Niedawne badania wykazały, że inne deskryptory - takie jak procent objętości zakopanej - są dokładniejsze niż kąt stożka w wychwytywaniu odpowiednich efektów sterycznych ligandu (ligandów) fosfinowego, gdy jest on związany z metalowym środkiem.
Zobacz też
- Kąt zgryzu
- Efekty steryczne (w porównaniu z efektami elektronicznymi)
- Parametr elektroniczny Tolmana