Model populacji

Model populacji to rodzaj modelu matematycznego stosowanego do badania dynamiki populacji .

Racjonalne uzasadnienie

Modele pozwalają lepiej zrozumieć, jak działają złożone interakcje i procesy. Modelowanie dynamicznych interakcji w przyrodzie może zapewnić łatwy sposób zrozumienia, jak liczby zmieniają się w czasie lub w stosunku do siebie. Wykorzystując model populacji jako narzędzie, można zauważyć wiele wzorców.

Ekologiczne modelowanie populacji dotyczy zmian parametrów, takich jak wielkość populacji i rozkład wieku w populacji. Może to wynikać z interakcji ze środowiskiem, osobnikami własnego gatunku lub innymi gatunkami.

Modele populacyjne służą do określania maksymalnych zbiorów dla rolników, zrozumienia dynamiki inwazji biologicznych oraz do ochrony środowiska . Modele populacyjne są również wykorzystywane do zrozumienia rozprzestrzeniania się pasożytów, wirusów i chorób .

Innym sposobem, w jaki modele populacji są przydatne, jest sytuacja, gdy gatunki stają się zagrożone. Modele populacji mogą śledzić delikatne gatunki i działać oraz ograniczać ich spadek. [1]

Historia

Biolodzy pod koniec XVIII wieku zaczęli opracowywać techniki modelowania populacji, aby zrozumieć dynamikę wzrostu i kurczenia się wszystkich populacji organizmów żywych. Thomas Malthus jako jeden z pierwszych zauważył, że populacja rosła według wzoru geometrycznego, kontemplując los ludzkości. Jednym z najbardziej podstawowych i przełomowych modeli wzrostu populacji był logistyczny model wzrostu populacji sformułowany przez Pierre'a François Verhulsta w 1838 roku. Model logistyczny ma kształt krzywej sigmoidalnej i opisuje wzrost populacji jako wykładniczy, po którym następuje spadek wzrostu i ograniczony nośnością ze względu na presję środowiskową.

Raymond Pearl zauważył presję na ograniczone środki utrzymania wynikającą ze wzrostu populacji ludzkiej w niektórych częściach Europy . W 1921 roku Pearl zaprosił fizyka Alfreda J. Lotkę do pomocy w jego laboratorium. Lotka opracowała sparowane równania różniczkowe , które pokazały wpływ pasożyta na jego ofiarę. Matematyk Vito Volterra utożsamił związek między dwoma gatunkami niezależnymi od Lotki. Lotka i Volterra wspólnie stworzyły model Lotki – Volterry dla konkurencji, która stosuje równanie logistyczne do dwóch gatunków, ilustrując interakcje między gatunkami w zakresie konkurencji, drapieżnictwa i pasożytnictwa. W 1939 roku Patrick Leslie wniósł wkład w modelowanie populacji, rozpoczynając pracę w biomatematyce. Leslie podkreślił znaczenie skonstruowania tabeli trwania życia, aby zrozumieć wpływ, jaki kluczowe strategie dotyczące historii życia odgrywają na dynamikę całych populacji. Algebra macierzowa została wykorzystana przez Lesliego w połączeniu z tablicami trwania życia, aby rozszerzyć pracę Lotki. Modele macierzowe populacji obliczają wzrost populacji na podstawie zmiennych dotyczących historii życia. Później Roberta MacArthura i EO Wilson scharakteryzowali biogeografię wyspy. Model równowagi biogeografii wysp opisuje liczbę gatunków na wyspie jako równowagę imigracji i wymierania. Logistyczny model populacji, model ekologii społeczności Lotki-Volterry, modelowanie macierzowe tabeli życia, model równowagi biogeografii wysp i ich odmiany są dziś podstawą ekologicznego modelowania populacji.

Równania

wzrostu logistycznego :

${\ Displaystyle {\ Frac {dN} {dt}} = rN \ lewo (1 - {\ Frac {N} {K}} \ prawo) \,}$

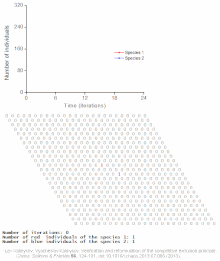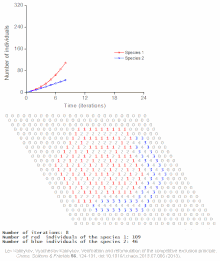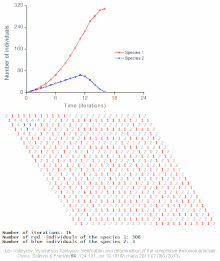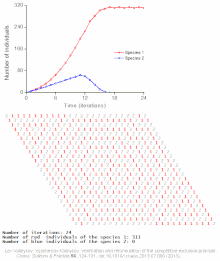
Konkurencyjne równania Lotki – Volterry :

${\ Displaystyle {\ Frac {dN_ {1}} {dt}} = r_ {1} N_ {1} {\ Frac { K_{1}-N_{1}-\alfa N_{2}}{K_{1}}}\,}$

Biogeografia wyspy :

${\ Displaystyle S = {\ Frac {IP} {I + E}}}$

Relacja gatunek–obszar :

${\ Displaystyle \ log (S) = \ log (c) + z \ log (A) \,}$

Przykłady modeli indywidualnych

Logiczny deterministyczny, indywidualny model automatów komórkowych ekosystemu z jednym gatunkiem. Model demonstruje mechanizm wzrostu populacji w kształcie litery S.

Logiczny deterministyczny, indywidualny model automatów komórkowych międzygatunkowej konkurencji o pojedynczy ograniczony zasób. Mechanizm konkurencyjnego wykluczania jednego gatunku przez inny.

Zobacz też

• Dynamika populacji
• Dynamika populacji rybołówstwa
• Ekologia populacji
• Zamknięcie chwili

Linki zewnętrzne

• Sieć wymiany kodów GreenBoxes . Greenboxes (Beta) to repozytorium kodu modelowania populacji typu open source. Greenboxy pozwalają użytkownikom w łatwy sposób udostępniać swój kod i wyszukiwać udostępniony kod innym osobom.