Ortoptyczny (geometria)

Aby zapoznać się z gałęzią medycyny, zobacz Ortoptyka .

W geometrii krzywych ortoptyka to zbiór punktów, dla których dwie styczne danej krzywej spotykają się pod kątem prostym.

  Parabola

  Ortoptyka paraboli (jej kierownica )

  Elipsa

  Ortoptyka elipsy (jej koło kierujące )

   Minimalna ramka ograniczająca elipsy ( opisana okręgiem ortoptycznym)

   Osie większe i mniejsze elipsy

  Hiperbola

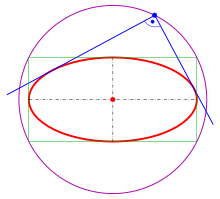
 Ortoptyka hiperboli (jej koło kierujące)

   xy i asymptoty hiperboliczne

Przykłady:

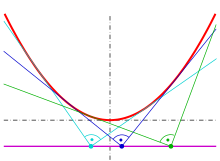
1. Ortoptyka paraboli to jej kierownica (dowód: patrz poniżej ),
2. Ortoptyka elipsy x $\ Displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1}$ to koło reżysera ${\ Displaystyle x ^ {2} + y ^ {2} = a ^ {2} + b ^ {2} }$ (patrz poniżej ),
3. Ortoptyka hiperboli x $\ Displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} - {\ tfrac {y ^ {2} }} {b ^ {2}}} = 1, \ a> b}$ to koło reżysera ${\ Displaystyle x ^ {2} + y ^ {2} = a ^ {2}-b^{2}}$ (w przypadku a ≤ b nie ma stycznych ortogonalnych, patrz poniżej ),
4. Ortoptyka astroidy $_$ r _ _ ${\ Displaystyle R = {\ tfrac {1} {\ sqrt {2}}} \ cos (2 \ varphi), \ 0 \ równoważnik \ varphi <2 \ pi} ($ patrz poniżej ).

uogólnienia:

1. Izoptyka to zbiór punktów, w których dwie styczne danej krzywej przecinają się pod ustalonym kątem (patrz poniżej ).
2. Izoptyka dwóch płaskich krzywych to zbiór punktów, w których dwie styczne przecinają się pod ustalonym kątem .
3. Twierdzenie Talesa o cięciwie PQ można uznać za ortoptykę dwóch okręgów zdegenerowanych do dwóch punktów P i Q .

Ortoptyka paraboli

Dowolną parabolę można przekształcić sztywnym ruchem (kąty się nie zmieniają) w parabolę z równaniem ${\ Displaystyle y = ax ^ {2}}$ . Nachylenie w punkcie paraboli wynosi ${\ Displaystyle m = 2ax}$ . Zastąpienie x daje parametryczną reprezentację paraboli z nachyleniem stycznej jako parametrem: ${\ Displaystyle \ \ lewo ({\ tfrac {m} {2a}}, {\ tfrac {m ^ {2}} {4a}} \ prawej) \!.} Styczna$ ma równanie ${\ Displaystyle y = mx + n}$ z wciąż nieznanym n , które można określić, wstawiając współrzędne punktu paraboli. Otrzymuje się ${\ Displaystyle \ y = mx - {\ tfrac {m ^ {2}} {4a}} \;.}$

Jeśli styczna zawiera punkt ₀₀ ( x , y ) poza parabolą, to równanie

${\ Displaystyle y_ {0} = mx_ {0} - {\ Frac {m ^ {2}} {4a}} \ quad \rightarrow \quad m^{2}-4ax_{0}\;m+4ay_{0}=0}$

trzyma, który ma dwa rozwiązania m ₁ i m ₂ odpowiadające dwóm przechodzącym stycznym ₀₀ ( x , y ) . Wolny termin zredukowanego równania kwadratowego jest zawsze iloczynem jego rozwiązań. Stąd, jeśli styczne spotykają się w punkcie ₀₀ ( x , y ) ortogonalnie, zachodzą następujące równania:

${\ Displaystyle m_ {1} m_ {2} = -1 = 4ay_ {0}}$

Ostatnie równanie jest równoważne

${\ Displaystyle y_ {0} = - {\ Frac {1} {4a}} \;,}$

co jest równaniem na kierownicę .

Ortoptyka elipsy i hiperboli

Elipsa

Główny artykuł: Koło reżyserskie

mi ${\ Displaystyle \; E: \; {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^$ będzie rozważaną elipsą.

(1) Styczne do elipsy $wierzchołkach$ i ko-wierzchołkach przecinają się w 4 punktach ${\ Displaystyle (\ pm a, \ pm b)}$ pożądana krzywa ortoptyczna (okrąg ${\ Displaystyle x ^ {2} + y ^ {2} = a ^ {2} + b ^ {2}} )$ .

$tfrac {u}{a^{2}}}x+{\tfrac {v}{b^{2}}}y=1}$ ) Styczna w punkcie ma ${$ u $=$$\$ (patrz styczna do elipsy ). Jeśli punkt nie jest wierzchołkiem, równanie to można rozwiązać dla y: ${\ Displaystyle \ y = - {\ tfrac {b ^ {2} u} {a ^ {2} v}} \; x \; + \; {\ tfrac {b ^ {2}} {v}} \ ;.}$

$Displaystyle (I) \; m = - {\ tfrac {b ^ {2} u} {a ^ {2} v }},\;{\color {red}n={\tfrac {b^{2}}{v}}}\;} i$ ja równanie ${\ Displaystyle \; {\ color {niebieski} {\ tfrac {u ^ {2}} {a ^ {2}}} = 1- {\ tfrac {v ^ {2}} {b ^ {2}}} =1-{\tfrac {b^{2}}{n^{2}}}}\;}$ otrzymujemy:

${\ Displaystyle m ^ {2} = {\ Frac {b ^ {4} u ^ {2}} {a ^ {4} v ^ {2}}} = {\ Frac {1} {a ^ {2} }}{\color {red}{\frac {b^{4}}{v^{2}}}}{\color {niebieski}{\frac {u^{2}}{a^{2}} }}={\frac {1}{a^{2}}}{\color {red}n^{2}}{\color {niebieski}(1-{\frac {b^{2}}{n ^{2}}})}={\frac {n^{2}-b^{2}}{a^{2}}}\;.}$

Stąd ${\ Displaystyle \ (II) \; n = \ pm {\ sqrt {m ^ {2} a ^ {2} + b ^ {2}}} }$ i równanie niepionowej stycznej to

${\ Displaystyle y = m \; x \; \ pm {\ sqrt {m ^ {2} a ^ {2} + b ^ {2}}}.}$

Rozwiązywanie relacji dla ${\ Displaystyle (I)}$ dla ${\ displaystyle u, v}$ i przestrzeganie ${\ Displaystyle (II)}$ prowadzi do zależnej od nachylenia parametrycznej reprezentacji elipsy

${\ Displaystyle (u, v) = (- {\ tfrac {ma ^ {2}}} {\ pm {\ sqrt {m ^ {2} a ^ {2} + b ^ {2}}}}} \; ,\;{\tfrac {b^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}})\ .\ } (Kolejny dowód$ : patrz Elipsa ).

$zawiera$ punkt elipsą,

${\ Displaystyle y_ {0} = mx_ {0} \ pm {\ sqrt {m ^ {2} a ^ {2} + b ^ {2}}}}$

posiada. Wyeliminowanie pierwiastka kwadratowego prowadzi do

${\ Displaystyle m ^ {2} - {\ Frac {2x_ {0} y_ {0}} {x_ { 0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}} }=0,}$

${\ Displaystyle (x_ {0}$ dwa rozwiązania odpowiadające dwóm stycznym przechodzącym przez $x$ . Stały wyraz monicznego równania kwadratowego jest zawsze iloczynem jego rozwiązań. Stąd, jeśli styczne spotykają się ortogonalnie, zachodzą następujące równania: ${\ Displaystyle (x_ {0}, y_ {0})}$

Ortoptyka (czerwone kółka) koła, elips i hiperboli

${\ Displaystyle m_ {1} m_ {2} = - 1 = {\ Frac {y_ {0} ^ {2} -b ^ {2 }}{x_{0}^{2}-a^{2}}}}$

Ostatnie równanie jest równoważne

${\ Displaystyle x_ {0} ^ {2} + y_ {0} ^ {2} = a ^ {2} + b ^ {2} \;.}$

Z (1) i (2) otrzymujemy:

• Punkty przecięcia stycznych ortogonalnych są punktami okręgu ${\ Displaystyle x ^ {2} + y ^ {2} = a ^ {2} + b ^ {2}}$ .

Hiperbola

Przypadek elipsy można prawie dokładnie zaadaptować do przypadku hiperboli. Jedyne zmiany, które należy wprowadzić, to zastąpienie ${2} }$ 2 $b ^$ displaystyle i ograniczenie m | m | > b / a . Dlatego:

• Punkty przecięcia stycznych ortogonalnych są punktami okręgu ${\ Displaystyle x ^ {2} + y ^ {2} = a ^ {2} -b ^ {2}}$ , gdzie a > b .

Ortoptyka astroidy

Ortoptyczny (fioletowy) astroidy

Astroidę można opisać reprezentacją parametryczną

${\ Displaystyle {\ vec {c}} (t) = \ lewo (\ sałata ^ {3} t \ grzech ^{3}t\prawo),\quad 0\równik t<2\pi }$ .

Od warunku

${\ Displaystyle {\ vec {\ kropka {c}}} (t) \ cdot {\ vec {\ kropka {c}}} (t + \ alfa )=0}$

rozpoznaje się odległość α w przestrzeni parametrów, przy której pojawia się ortogonalna styczna do ċ → ( t ) . Okazuje się, że odległość jest niezależna od parametru t , czyli α = ± π / 2 . Równania stycznych (ortogonalnych) w punktach c → ( t ) i c → ( t + π / 2 ) są odpowiednio:

${\ Displaystyle {\ rozpocząć {wyrównane} y & = - \ tan t \ lewo (x- \ cos ^ {3} t \ prawej) + \ sin ^ {3} t, \\ y & = {\ frac {1} \tan t}}\left(x+\sin ^{3}t\right)+\cos ^{3}t.\end{wyrównane}}}$

Ich wspólny punkt ma współrzędne:

${\ Displaystyle {\ rozpocząć {wyrównane} x & = \ sin t \ cos t (\ sin t- \ cos t), \\ y & = \ sin t \ cos t (\ sin t + \ cos t). \ koniec {wyrównane }}}$

Jest to jednocześnie parametryczna reprezentacja ortoptyki.

Eliminacja parametru t daje niejawną reprezentację

${\ Displaystyle 2 \ lewo (x ^ {2} + y ^ {2} \ prawo) ^ {3} - \ lewo ( x^{2}-y^{2}\prawo)^{2}=0.}$

Wprowadzenie nowego parametru φ = t − 5π / 4 jeden dostaje

${\ Displaystyle {\ rozpocząć {wyrównane} x & = {\ tfrac {1} {\ sqrt {2}}} \ cos (2 \ varphi) \ cos \ varphi, \\ y& = {\ tfrac {1} {\ sqrt {2}}}\cos(2\varphi )\sin \varphi .\end{wyrównane}}}$

(Dowód wykorzystuje tożsamość sumy i różnicy kątów .) Otrzymujemy zatem reprezentację biegunową

${\ Displaystyle R = {\ tfrac {1} {\ sqrt {2}}} \ cos (2 \ varphi), \ quad 0 \ równoważnik \ varphi <2\pi}$

ortoptycznego. Stąd:

• Ortoptyka astroidu to quadrifolium .

Izoptyka paraboli, elipsy i hiperboli

Isoptics (fioletowe) paraboli dla kątów 80° i 100°

Izoptyki (fioletowe) elipsy dla kątów 80° i 100°

Isoptics (fioletowe) hiperboli dla kątów 80° i 100°

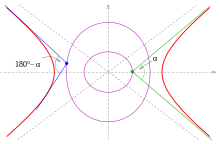
wymieniono izotopy dla kątów α ≠ 90 ° . Nazywa się je izooptykami α . Dowody znajdują się poniżej .

Równania izotopów

Parabola:

Izooptyki α paraboli z równaniem y = ax ² są gałęziami hiperboli

${\ Displaystyle x ^ {2} - \ dębnik ^ {2} \ alfa \ lewo (y + {\ Frac {1} {4a }}\right)^{2}-{\frac {y}{a}}=0.}$

Gałęzie hiperboli dostarczają izooptyki dla dwóch kątów α i 180° − α (patrz rysunek).

Elipsa:

Izooptyki α elipsy z równaniem x ² / a ² + y ² / b ² = 1 to dwie części krzywej stopnia-4

${\ Displaystyle \ lewo (x ^ {2} + y ^ {2}-a^{2}-b^{2}\right)^{2}\tan ^{2}\alpha =4\left(a^{2}y^{2}+b^{2 }x^{2}-a^{2}b^{2}\prawo)}$

(widzieć zdjęcie).

Hiperbola:

Izooptyki α hiperboli z równaniem x ² / a ² − y ² / b ² = 1 to dwie części krzywej stopnia 4

${\ Displaystyle \ lewo (x ^ {2} + y ^ {2} -a ^ {2} + b ^ {2} \ prawo) ^ {2} \ tan ^ {2} \ alfa = 4 \ lewo (a ^{2}y^{2}-b^{2}x^{2}+a^{2}b^{2}\prawo).}$

Dowody

Parabola:

Parabola y = ax ² może być sparametryzowana przez nachylenie jej stycznych m = 2 ax :

${\ Displaystyle {\ vec {c}} (m) = \ lewo ({\ Frac {m} {2a}}, {\ Frac {m ^ {2}} {4a}} \ prawej), \ quad m \ w \mathbb {R} .}$

Styczna o nachyleniu m ma równanie

${\ Displaystyle y = mx - {\ Frac {m ^ {2}} {4a}}.}$

Punkt ₀₀ ( x , y ) leży na stycznej wtedy i tylko wtedy, gdy

${\ Displaystyle y_ {0} = mx_ {0} - {\ Frac {m ^ {2}} {4a}}.}$

Oznacza to, że współczynniki kierunkowe m ₁ , m ₂ dwóch stycznych zawierających ₀₀ ( x , y ) spełniają równanie kwadratowe

${\ Displaystyle m ^ {2} -4ax_ {0} m + 4ay_ {0} = 0.}$

Jeśli styczne spotykają się pod kątem α lub 180° − α , równanie

${\ Displaystyle \ dębnik ^ {2} \ alfa = \ lewo ({\ Frac {m_ {1} -m_ {2}} {1 +m_{1}m_{2}}}\prawo)^{2}}$

musi być spełniony. Rozwiązując równanie kwadratowe dla m i podstawiając m ₁ , m ₂ do ostatniego równania, otrzymujemy

${\ Displaystyle x_ {0} ^ {2} - \ dębnik ^ {2} \ alfa \ lewo (y_ {0} + { \frac {1}{4a}}\right)^{2}-{\frac {y_{0}}{a}}=0.}$

To jest równanie powyższej hiperboli. Na jej gałęziach znajdują się dwie izooptyki paraboli dla dwóch kątów α i 180° − α .

Elipsa:

W przypadku elipsy x ² / a ² + y ² / b ² = 1 można przyjąć ideę ortoptyki dla równania kwadratowego

${\ Displaystyle m ^ {2} - {\ Frac {2x_ {0} y_ {0}} {x_ {0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2} }}=0.}$

Teraz, podobnie jak w przypadku paraboli, należy rozwiązać równanie kwadratowe i wstawić do równania dwa rozwiązania m ₁ , m ₂

${\ Displaystyle \ tan ^ {2} \ alfa = \ lewo ({\ Frac {m_ {1} -m_ {2}} {1 + m_ {1} m_ {2}}} \ prawej) ^ {2}. }$

Zmiana układu pokazuje, że izooptyki są częściami krzywej stopnia 4:

${\ Displaystyle \ lewo (x_ {0} ^ {2} + y_ {0} ^ {2} -a ^ {2} -b ^ {2} \ prawo) ^ {2} \ tan ^ {2} \ alfa =4\left(a^{2}y_{0}^{2}+b^{2}x_{0}^{2}-a^{2}b^{2}\right).}$

Hiperbola:

Rozwiązanie dla przypadku hiperboli można przyjąć z przypadku elipsy, zastępując b ² przez - b ² (jak w przypadku ortoptyki, patrz wyżej ).

Aby zwizualizować izooptyki, zobacz krzywą niejawną .

Linki zewnętrzne

• Specjalne krzywe płaszczyzny.
• Świat matematyki
• Krzywe Jana Wassenaara
• „Izoptyczna krzywa” w MathCurve
• „Krzywa ortoptyczna” w MathCurve

Notatki

•   Lawrence, J. Dennis (1972). Katalog specjalnych krzywych płaskich . Publikacje Dover. s. 58–59 . ISBN 0-486-60288-5 .
• Odehnal, Borys (2010). „Krzywe równooptyczne przekrojów stożkowych” (PDF) . Czasopismo dla geometrii i grafiki . 14 (1): 29–43.
•   Schaal, Hermann (1977). Algebra liniowa i geometria analityczna . Tom. III. Wyświetleg. P. 220. ISBN 3-528-03058-5 .
• Steiner, Jakub (1867). Vorlesungen über synthetische Geometrie . Lipsk: BG Teubner. Część 2, s. 186.
•   Ternullo, Maurizio (2009). „Dwa nowe zestawy punktów koncyklicznych związanych z elipsami”. Dziennik geometrii . 94 (1–2): 159–173. doi : 10.1007/s00022-009-0005-7 . S2CID 120011519 .