Krzywa równoległa

Nie mylić z transportem równoległym .

Równoległe krzywe wykresu ${\ Displaystyle y = 1,5 \ sin (x)}$ dla odległości ${\ Displaystyle d = 0,25, \ kropki, 1,5}$

Dwie definicje krzywej równoległej: 1) obwiednia rodziny przystających okręgów, 2) ustalona normalna odległość

Równoległe krzywe koła (kolor czerwony) również są okręgami

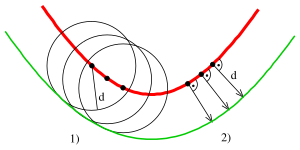
Równoległość krzywej to obwiednia rodziny przystających okręgów wyśrodkowanych na krzywej . Uogólnia koncepcję linii równoległych (prostych) . Można ją również zdefiniować jako krzywą, której punkty znajdują się w stałej normalnej odległości od danej krzywej. Te dwie definicje nie są całkowicie równoważne, ponieważ ta druga zakłada gładkość , podczas gdy pierwsza nie.

W projektowaniu wspomaganym komputerowo preferowanym terminem określającym krzywą równoległą jest krzywa przesunięta . (W innych kontekstach geometrycznych termin przesunięcie może również odnosić się do przesunięcia ). Krzywe przesunięcia są ważne na przykład w obróbce sterowanej numerycznie , gdzie opisują na przykład kształt cięcia wykonanego przez okrągłe narzędzie skrawające maszyny dwuosiowej. Kształt cięcia jest odsunięty od trajektorii frezu o stałą odległość w kierunku normalnym do trajektorii frezu w każdym punkcie.

W dziedzinie grafiki komputerowej 2D, znanej jako grafika wektorowa , (przybliżone) obliczanie równoległych krzywych jest zaangażowane w jedną z podstawowych operacji rysowania, zwaną obrysowywaniem, która jest zwykle stosowana do polilinii lub polibezierów (zwanych ścieżkami) w tej dziedzinie.

Z wyjątkiem przypadku linii lub okręgu , krzywe równoległe mają bardziej skomplikowaną strukturę matematyczną niż krzywa progenitorowa. Na przykład, nawet jeśli krzywa przodka jest gładka , jej przesunięcia mogą nie być takie; ta właściwość jest zilustrowana na górnym rysunku, przy użyciu krzywej sinusoidalnej jako krzywej progenitorowej. Ogólnie rzecz biorąc, nawet jeśli krzywa jest wymierna , jej przesunięcia mogą nie być takie. Na przykład przesunięcia paraboli są krzywymi wymiernymi, ale przesunięcia elipsy lub hiperboli nie są wymierne, chociaż same te krzywe progenitorowe są wymierne.

Pojęcie to odnosi się również do powierzchni 3D , gdzie jest nazywane powierzchnią przesuniętą lub powierzchnią równoległą . Zwiększenie objętości bryły o (stałe) przesunięcie odległości jest czasami nazywane dylatacją . Odwrotna operacja jest czasami nazywana ostrzałem . Powierzchnie offsetowe są ważne w obróbce sterowanej numerycznie , gdzie opisują kształt skrawania wykonanego przez kulisty frez trzpieniowy maszyny trójosiowej. Inne kształty ostrzy skrawających można modelować matematycznie za pomocą ogólnych powierzchni przesuniętych.

Krzywa równoległa do krzywej zadanej parametrycznie

Jeśli istnieje regularna reprezentacja parametryczna danej krzywej dostępna, ${\ Displaystyle {\ vec {x}} = (x (t), y (t))}$ druga definicja krzywej równoległej (patrz powyżej) prowadzi do następującej reprezentacji parametrycznej krzywej równoległej z odległością ${\ Displaystyle | d|}$ :

${\ Displaystyle {\ vec {x}} _ {d} (t) = {\ vec {x}} (t) + d { \ vec {n}} (t)}$ z jednostką normalną ${\ Displaystyle {\ vec {n}} (t)}$ .

We współrzędnych kartezjańskich:

$\ Displaystyle x_ {d} (t) = x (t) + {\ Frac { d\;y'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}}$

${\ Displaystyle y_ {d} (t) = y (t) - {\ Frac {d \; x' (t)}} {\ sqrt {x' (t) ^ {2} + y' (t) ^ { 2}}}}\ .}$

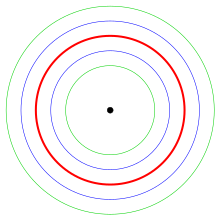
Parametr odległości $ujemny$ . W tym przypadku uzyskuje się równoległą krzywą po przeciwnej stronie krzywej (patrz diagram równoległych krzywych okręgu). Można łatwo sprawdzić, że równoległa krzywa prostej jest w zdrowym rozsądku linią równoległą, a równoległa krzywa okręgu jest kołem koncentrycznym.

Właściwości geometryczne:

• ${\ Displaystyle {\ vec {x}} '_ {d} (t) \ równolegle {\ vec {x}} '(t), \ quad}$ to znaczy: wektory styczne dla ustalonego parametru są równoległe.
• ${\ Displaystyle k_ {d} (t) = {\ Frac {k (t)} {1 + dk (t)}} \ quad }$ z krzywizną danej krzywej i $\ Displaystyle$$}$ d } ( krzywizną równoległej krzywej dla parametru $\ displaystyle t }$ .
• ${\ Displaystyle R_ {d} (t) = R (t) + d, \ quad}$ z promieniem $R (t)}$ Displaystyle krzywizna danej krzywej i promień krzywizny równoległej krzywej dla parametru $\ Displaystyle$$R_ {d} ( t)}$ .
• Kiedy istnieją, oscylujące okręgi do równoległych krzywych w odpowiednich punktach są koncentryczne.
• Jeśli chodzi o linie równoległe , prosta normalna do krzywej jest również normalna do jej równoleżników.
• Podczas konstruowania równoległych krzywych będą one miały wierzchołki , gdy odległość od krzywej odpowiada promieniowi krzywizny . Są to punkty, w których krzywa styka się z ewolutą .
• Jeśli krzywa progenitorowa jest granicą zbioru planarnego, a jej równoległa krzywa nie ma samoprzecięć, to ta ostatnia jest granicą sumy Minkowskiego zbioru planarnego i dysku o zadanym promieniu.

Jeśli dana krzywa jest wielomianem (co oznacza, że $wówczas$$)$ , równoległe zwykle W obszarze CAD jest to wada, ponieważ systemy CAD wykorzystują wielomiany lub krzywe wymierne. Aby otrzymać przynajmniej krzywe wymierne, pierwiastek kwadratowy reprezentacji krzywej równoległej musi być rozwiązywalny. Takie krzywe nazywane są pitagorejskimi krzywymi hodografowymi i zostały zbadane przez RT Farouki.

Równoległe krzywe krzywej domniemanej

Równoległe krzywe krzywej domniemanej (czerwonej) z równaniem ${\ Displaystyle x ^ {4} + y ^ {4} -1 = 0}$

Ogólnie analityczna reprezentacja krzywej równoległej krzywej domniemanej nie jest możliwa. Tylko w prostych przypadkach linii i okręgów krzywe równoległe można łatwo opisać. Na przykład:

Linia ${\ Displaystyle \; f (x, y) = x + y-1 = 0 \;}$ → funkcja odległości: ${\ Displaystyle \; h (x, y) = {\ Frac {x + y-1} {\ sqrt {2}}} = d \;} (forma normalna Hessego$ )

Koło ${\ Displaystyle \; f (x, y) = x ^ {2} + y ^ {2} -1 = 0 \;}$ → funkcja odległości: ${\ Displaystyle \; h (x, y) = {\ sqrt {x ^ {2} + y ^ {2}}} -1 = d \;.}$

Ogólnie, zakładając pewne warunki, można udowodnić istnienie zorientowanej funkcji odległości. godz ${\ displaystyle h (x, y)$ . W praktyce trzeba to traktować numerycznie. Biorąc pod uwagę równoległe krzywe, następujące stwierdzenie jest prawdziwe:

• Równoległa $.$$_$ ustawionym dla odpowiedniej

Własności funkcji odległości:

• ${\ Displaystyle | \ nazwa operatora {grad} h ({\ vec {x}}) | = 1 \;,}$
• ${\ Displaystyle h ({\ vec {x}} + d \ operatorname {grad} h ({\ vec {x} }))=h({\vec {x}})+d\;,}$
• ${\ Displaystyle \ nazwa operatora {grad} h ({\ vec {x}} + d \ nazwa operatora {grad} h ({\ vec {x}})) = \ nazwa operatora {grad} h ({\ vec {x}} )\;.}$

Przykład: Diagram przedstawia równoległe krzywe krzywej domniemanej z równaniem ${\ Displaystyle \; f (x, y) = x ^ {4} + y ^ {4} -1 = 0 \;.}$ Uwaga: krzywe ${\ Displaystyle \; f (x, y) = x ^ {4} + y ^ {4} -1 = d \;}$ nie są krzywymi równoległymi, ponieważ ${\ Displaystyle \;|\ operatorname {grad} f (x, y) | = 1 \;}$ nie jest prawdziwe w obszarze zainteresowania.

Dalsze przykłady

Ewolwenty koła

• Ewolwenty danej krzywej są zbiorem krzywych równoległych. Na przykład: ewolwenty koła są równoległymi spiralami (patrz diagram).

I:

• Parabola ma jako (dwustronne) przesunięcia wymierne krzywe stopnia 6.
• Hiperbola lub elipsa ma jako (dwustronne) przesunięcie krzywą algebraiczną stopnia 8.
• Krzywa Béziera stopnia n ma as (dwustronne) przesunięcia krzywych algebraicznych stopnia 4 n - 2 . W szczególności sześcienna krzywa Beziera ma (dwustronne) przesunięcia krzywych algebraicznych stopnia 10.

Krzywa równoległa do krzywej z narożnikiem

Równoległe krzywe do krzywej z nieciągłą normalną za rogiem

Podczas określania ścieżki skrawania części z ostrym narożem do obróbki należy zdefiniować krzywą równoległą (odsuniętą) do danej krzywej, która ma nieciągłą normalną w narożu. Nawet jeśli dana krzywa nie jest gładka w ostrym rogu, jej równoległa krzywa może być gładka z ciągłą normalną lub może mieć wierzchołki , gdy odległość od krzywej odpowiada promieniowi krzywizny w ostrym rogu.

Normalni kibice

Jak opisano powyżej ${\vec {x}}(t)}$ parametryczna reprezentacja krzywej równoległej danej krzywej jest $vec {x}} _ {d} ($$\$ , z odległością ${\ displaystyle | d |}$ to:

${\ Displaystyle {\ vec {x}} _ {d} (t) = {\ vec {x}} (t) + d { \ vec {n}} (t)}$ z jednostką normalną ${\ Displaystyle {\ vec {n}} (t)}$ .

Na ostrym rogu ( $do$ normalna do ${\ Displaystyle {\ vec {x}} (t_ {c}$ podana ${\ Displaystyle {\ vec {n}} (t_ {c})}$ jest nieciągły, co oznacza jednostronną granicę normalnej z lewej strony ${\ Displaystyle {\ vec {n}}(t_{c}^{-})}$ jest nierówne do granicy z prawej strony ${\ Displaystyle {\ vec {n}} (t_ {c} ^ {+})}$ . Matematycznie,

${\ Displaystyle {\ vec {n}} ( t_{c}^{-})=\lim _{t\to t_{c}^{-}}{\vec {n}}(t)\neq {\vec {n}}(t_{c} ^{+})=\lim _{t\to t_{c}^{+}}{\vec {n}}(t)}$ .

Normalny wachlarz do wyznaczania równoległych krzywych wokół ostrego narożnika

Możemy jednak zdefiniować normalny $\ vec {n}} (t_ {c} ^ {-})}$$który$ interpolant n → i ${\ Displaystyle {\ vec {n}} (t_ {c} ^ {+})}$ i użyj ${\ Displaystyle {\ vec {n}} _ {f} (\ alfa)}$ zamiast ${\ Displaystyle {\ vec {n}} (t_ {c})}$ w ostrym rogu:

${\ Displaystyle {\ vec {n}} _ {f} (\ alfa) = {\ Frac {(1- \ alfa) {\ vec {n}} (t_ {c} ^ {-}) + \ alfa { \vec {n}}(t_{c}^{+})}{\lVert (1-\alpha ){\vec {n}}(t_{c}^{-})+\alpha {\vec { n}} (t_ {c} ^ {+}) \ rVert}} \ quad}$ gdzie ${\ Displaystyle 0 <\ alfa <1}$ .

Wynikowa definicja krzywej równoległej zapewnia pożądane zachowanie: ${\ displaystyle {\ vec {x}} _ {d} (t)}$

${\ Displaystyle {\ vec {x}} _ {d} (t) = {\ rozpocząć {przypadki} {\ vec {x}} (t) + d {\ vec {n}} (t) ,&{\text{if }}t<t_{c}{\text{ lub }}t>t_{c}\\{\vec {x}}(t_{c})+d{\vec {n }}_{f}(\alpha ),&{\text{if }}t=t_{c}{\text{ gdzie }}0<\alpha <1\end{przypadki}}}$

Algorytmy

Ogólnie rzecz biorąc, równoległa krzywa krzywej Béziera nie jest kolejną krzywą Béziera, co udowodnili Tiller i Hanson w 1984 r. Dlatego w praktyce stosuje się techniki aproksymacji. Dowolny pożądany poziom dokładności jest możliwy poprzez wielokrotne dzielenie krzywej, chociaż lepsze techniki wymagają mniejszej liczby podziałów, aby osiągnąć ten sam poziom dokładności. Ankieta przeprowadzona w 1997 roku przez Elbera, Lee i Kima jest szeroko cytowana, chociaż ostatnio zaproponowano lepsze techniki. Nowoczesna technika oparta na dopasowaniu krzywej , z odniesieniami i porównaniami do innych algorytmów, a także kodu źródłowego JavaScript typu open source, został opublikowany we wpisie na blogu we wrześniu 2022 r.

Innym skutecznym algorytmem kompensacji jest podejście poziomowe opisane przez Kimmela i Brucksteina (1993).

Powierzchnie równoległe (przesunięte).

Powierzchnia offsetowa o złożonym nieregularnym kształcie

Powierzchnie odsunięte są ważne w obróbce sterowanej numerycznie , gdzie opisują kształt skrawania wykonanego przez kulisty frez trzpieniowy frezu trójosiowego. Jeśli istnieje regularna reprezentacja parametryczna ${\ Displaystyle {\ vec {x}} (u, v) = (x (u, v), y (u, v), z (u, v)}} dostępnej danej powierzchni, druga definicja$ a krzywa równoległa (patrz wyżej) uogólnia następującą reprezentację parametryczną powierzchni równoległej z odległością ${\ Displaystyle | d|}$ :

${\ Displaystyle {\ vec {x}} _ {d} (u, v) = {\ vec {x }}(u,v)+d{\vec {n}}(u,v)}$ z jednostką normalną ${\ Displaystyle {\ vec {n}} _ {d} (u, v) = {{{\ częściowe {\ vec {x}} \ ponad \ częściowe u} \ razy {\ częściowe {\ vec {x}} \over \partial v}} \over {|{{\partial {\vec {x}} \over \partial u}\times {\partial {\vec {x}} \over \partial v}}|}} }$ .

Parametr odległości $ujemny$ . W tym przypadku uzyskuje się równoległą powierzchnię po przeciwnej stronie powierzchni (patrz podobny diagram na równoległych krzywych koła). Łatwo sprawdzić: równoległa powierzchnia płaszczyzny jest w zdrowym rozsądku płaszczyzną równoległą, a równoległa powierzchnia kuli jest kulą koncentryczną.

Właściwości geometryczne:

• ${\ Displaystyle {\ częściowe {\ vec {x}} _ {d} \ ponad \ częściowe u} \ równoległy {\częściowy {\vec {x}} \ponad \częściowy u},\quad {\częściowy {\vec {x}}_{d} \ponad \częściowy v}\równoległy {\częściowy {\vec {x }} \over \partial v},\quad }$ to znaczy: wektory styczne dla ustalonych parametrów są równoległe.
• ${\ Displaystyle {\ vec {n}} _ {d} (u, v) = \ pm {\ vec {n}} (u, v),\quad }$ oznacza to, że wektory normalne dla ustalonych parametrów są zgodne z kierunkiem.
• ${\ Displaystyle S_ {d} = (1 + dS) ^ {- 1} S \ quad}$ gdzie ${\ Displaystyle S_ {d}}$ i $S}$${ \$${\ displaystyle {\ vec {x$ to kształtu odpowiednio dla i $}} _ {d}}$ .

Główne krzywizny to wartości własne operatora kształtu , główne kierunki krzywizny to jego wektory własne , krzywizna Gaussa jest jego wyznacznikiem , a średnia krzywizna to połowa jego śladu .

• ${\ Displaystyle S_ {d} ^ {- 1} = S ^ {- 1} + dI, \ quad}$ gdzie ${\ Displaystyle S_ {d} ^ {-1}}$ S ${\ Displaystyle S ^ {- 1}}$ są odwrotnościami operatorów kształtu dla ${\ Displaystyle {\ vec {x}} _ {d}}$ i $x}}}$${\ Displaystyle {\ vec {$ odpowiednio.

Główne promienie krzywizny to wartości własne odwrotności operatora kształtu , główne kierunki krzywizny to jego wektory własne , odwrotność krzywizny Gaussa jest jej wyznacznikiem , a średni promień krzywizny to połowa jego śladu .

Zwróć uwagę na podobieństwo do właściwości geometrycznych krzywych równoległych .

Uogólnienia

Problem uogólnia się w dość oczywisty sposób na większe wymiary, np. powierzchnie odsunięte, iw nieco mniej trywialny sposób na powierzchnie rur . Należy zauważyć, że terminologia dla wersji o wyższych wymiarach różni się jeszcze bardziej niż w przypadku planarnym, np. inni autorzy mówią o włóknach równoległych, wstęgach i rurkach. W przypadku krzywych osadzonych w powierzchniach 3D przesunięcie może być wykonane wzdłuż linii geodezyjnej .

Innym sposobem uogólnienia jest (nawet w 2D) rozważenie zmiennej odległości, np. sparametryzowanej przez inną krzywą. Można np. obrysować (obwiednię) elipsą zamiast okręgu, tak jak jest to możliwe np. w METAFONT .

Obwiednia elips tworzących dwie ogólne przesunięte krzywe powyżej i poniżej danej krzywej

Niedawno Adobe Illustrator dodał nieco podobną funkcję w wersji CS5 , chociaż punkty kontrolne dla zmiennej szerokości są określone wizualnie. W kontekstach, w których ważne jest rozróżnienie między przesunięciem stałej i zmiennej odległości, czasami używane są akronimy CDO i VDO.

Ogólne krzywe przesunięcia

Załóżmy, że masz regularną parametryczną reprezentację krzywej, ${\ Displaystyle {\ vec {x}} (t) = (x (t), y ( t))}$ i masz drugą krzywą, którą można sparametryzować za pomocą jej normalnej jednostki, ${\ Displaystyle {\ vec {d}} ({\ vec {n}})$ } z ${\ Displaystyle {\ vec {d}} ({\ vec {n}}) = {\ vec {n}}} ($ ta parametryzacja przez normalną istnieje dla krzywych, których krzywizna jest ściśle dodatnia lub ujemna, a zatem wypukła, gładka, a nie prosta). Parametryczna reprezentacja krzywej przesunięcia ogólnego przesunięcia ${$ { ${ d}$ to:

${\ Displaystyle {\ vec {x}} _ {d} (t) = {\ vec {x}} (t ) + {\ vec {d}} ({\ vec {n}} (t)), \ quad} gdzie n$ → $Displaystyle {\ vec {n}} (t)}$ jest normalną jednostką ${\ Displaystyle {\ vec {x}} (t)}$ .

$_$ przesunięcie _ (alias offset) krzywe.

Właściwości geometryczne:

• ${\ Displaystyle {\ vec {x}} '_ {d} (t) \ równolegle {\ vec {x}} '(t), \ quad}$ to znaczy: wektory styczne dla ustalonego parametru są równoległe.
• Podobnie jak w przypadku linii równoległych , normalna do krzywej jest również normalna do jej ogólnych przesunięć.
• $t)}}}}, \ quad}$${\ Displaystyle k_ {d} (t) = {\ dfrac {k (t)}} {1 + {\ dfrac {k (t)} {k_ {n}$ ( z ${\ Displaystyle k_ {d} (t)}$ krzywizną ogólnej krzywej przesunięcia, ${ \displaystyle k(t)}$ krzywizna ${\ Displaystyle {\ vec {x}} (t)}$ i ${\ Displaystyle k_ {n} (t)}$ krzywizna ${ \ displaystyle {\ vec {d}} ({\ vec {n}} (t))}$ dla parametru ${\ displaystyle t}$ .
• ${\ Displaystyle R_ {d} (t) = R (t) + R_ {n} (t), \ quad}$ z ${\ Displaystyle R_ {d} (t)}$ promień krzywizny ogólnej krzywej przesunięcia, ${\ Displaystyle R (t)}$ promień krzywizny ${\ Displaystyle {\ vec {x}} (t)}$ i ${\ Displaystyle R_ {n} (t)}$ promień krzywizny ${\ Displaystyle { \ vec {d}} ({\ vec {n}} (t))}$ dla parametru ${\ displaystyle t}$ .
• Podczas konstruowania ogólnych krzywych przesunięcia będą one miały wierzchołki , gdy krzywizna krzywej odpowiada krzywiźnie przesunięcia. Są to punkty, w których krzywa styka się z ewolutą .

Ogólne powierzchnie offsetowe

Ogólne powierzchnie offsetowe opisują kształt nacięć wykonanych przez różne końcówki skrawające stosowane przez trójosiowe frezy palcowe w obróbce sterowanej numerycznie . Załóżmy, że masz regularną parametryczną reprezentację powierzchni, ${\ Displaystyle {\ vec {x}} (u, v) = (x (u, v), y (u, v), z (u, v))} i masz drugą powierzchnię, którą można$ parametryzować przez jego normalną jednostkę $Displaystyle$$n$ → (ta parametryzacja przez normalną istnieje dla powierzchni, których krzywizna Gaussa jest ściśle dodatnia, a zatem wypukła, gładka, a nie płaska). Parametryczna reprezentacja ogólnej powierzchni przesunięcia ${\ Displaystyle {\ vec {x}} (t)}$ przesunięcie o ${\ Displaystyle {\ vec {d}} ({\ vec {n}})}$ to:

${\ Displaystyle {\ vec {x}} _ {d} (u, v) = { \ vec {x}} (u, v) + {\ vec {d}} ({\ vec {n}} (u, v)), \ quad} gdzie n → ($ u $\ vec {n}}(u,v)}$ jest normalną jednostką ${\ Displaystyle {\ vec {x}} (u, v)}$ .

$_$ przesunięcie _ (znane również jako offsetowe) powierzchnie.

Właściwości geometryczne:

• Jeśli chodzi o linie równoległe , płaszczyzna styczna powierzchni jest równoległa do płaszczyzny stycznej jej ogólnych przesunięć.
• Podobnie jak w przypadku linii równoległych , normalna do powierzchni jest również normalna do jej ogólnych przesunięć.
• ${\ Displaystyle S_ {d} = (1 + SS_ {n} ^ {- 1}) ^ {- 1} S \ quad}$ gdzie ${\ Displaystyle S_ {d}, S,}$ i ${\ Displaystyle S_ {n}}$ to operatory kształtu dla ${\ Displaystyle {\ vec {x}} _ {d },{\vec {x}},}$ i odpowiednio ${\ Displaystyle {\ vec {d}} ({\ vec {n}})}$

Główne krzywizny to wartości własne operatora kształtu , główne kierunki krzywizny to jego wektory własne , krzywizna Gaussa jest jego wyznacznikiem , a średnia krzywizna to połowa jego śladu .

• ${\ Displaystyle S_ {d} ^ {- 1} = S ^ {- 1} + S_ {n} ^ {- 1}, \ quad}$ gdzie ${\ Displaystyle S_ {d} ^ {- 1}, S ^ {- 1}}$ i ${\ Displaystyle S_ {n} ^ {- 1}}$ są odwrotnościami operatorów kształtu dla ${\ Displaystyle {\ vec {x}} _ {d}, {\ vec {x}},}$ i ${\ Displaystyle {\ vec {d}} ({\ vec {n}})}$ odpowiednio.

Główne promienie krzywizny są wartościami własnymi odwrotności operator kształtu , główne kierunki krzywizny są jego wektorami własnymi , odwrotność krzywizny Gaussa jest jej wyznacznikiem , a średni promień krzywizny to połowa jej śladu .

Zwróć uwagę na podobieństwo do właściwości geometrycznych ogólnych krzywych odsuniętych .

Wyprowadzanie własności geometrycznych dla offsetów ogólnych

Wymienione powyżej właściwości geometryczne ogólnych krzywych przesunięcia i powierzchni można wyprowadzić dla przesunięć o dowolnym wymiarze. $, że$ -wymiarowej powierzchni gdzie wymiar $displaystyle {\vec {u}}}$ wynosi n-1. Załóżmy również, że masz drugą n-wymiarową powierzchnię, którą można sparametryzować za pomocą jej normalnej jednostki, ${\ Displaystyle {\ vec {d}} ({\ vec {n}})}$ , gdzie normalna z ${\ Displaystyle {\ vec {d}} ({\ vec {n}}) = {\ vec {n}}}$ (ta parametryzacja przez normalną istnieje dla powierzchni którego krzywizna Gaussa jest ściśle dodatnia, a zatem wypukła, gładka, a nie płaska). Parametryczna reprezentacja ogólnej powierzchni przesunięcia przesunięcia o $→ ) {\ Displaystyle {\ vec {x}} ({\ vec {$ u ${\ Displaystyle {\ vec {d}} ({\ vec {n}})}$ jest:

${\ Displaystyle {\ vec {x}} _ {d} ({\ vec {u}}) = {\vec {x}}({\vec {u}})+{\vec {d}}({\vec {n}}({\vec {u}}),\quad }$ gdzie ${\ Displaystyle {\ vec {n}} ({\ vec {u}})}$ jest normalną jednostką ${\ Displaystyle {\ vec {x}} ({\ vec {u}})}$ . (Przesunięcie trywalne, ${\ Displaystyle {\ vec {d}} ({\ vec {n}}) = d {\ vec {n}}} ,$ daje zwykłe równoległe powierzchnie .)

${\ Displaystyle {\ vec {d}} ({\ vec {n}} ({\ vec {u}})) = {\ vec {n}} ({\ vec {u}} )}$$_$ że normalna z definicji. Teraz zastosujemy różnicę wrt ${\ displaystyle {\ vec {u}}$ } ${\ displaystyle {\ vec {x}} _ {d}}$ , co daje nam wektory styczne obejmujące jego płaszczyznę styczną.

${\ Displaystyle \ częściowe {\ vec {x}} _ {d} ({\ vec {u }})=\częściowy {\vec {x}}({\vec {u}})+\częściowy {\vec {d}}({\vec {n}}({\vec {u}})) }$

Zauważ, że wektory styczne dla $Displaystyle$${\ vec {x}} ({$ wektorów stycznych dla i jego przesunięcie, które mają tę samą normalną jednostkę. ${\ Displaystyle {\ vec {d}} ({\ vec {n}})}$ Zatem ogólna powierzchnia odsunięcia ma tę samą płaszczyznę styczną i normalną z ${\ Displaystyle {\ vec {x}} ({\ vec {u}})}$ i ${\ Displaystyle {\ vec {d}} ({\ vec {n}} ( {\vec {u}}))}$ . Jest to zgodne z naturą kopert.

Rozważymy teraz równania Weingartena dla operatora kształtu , który można zapisać jako ${\ Displaystyle \ częściowe {\ vec {n}} = - \ częściowe {\ vec {x}} S}$ . ${\ displaystyle S} jest$ odwracalny , ${\ Displaystyle \ częściowe {\ vec {x}} = - \ częściowe {\ vec {n}} S ^ {- 1} }$ . Przypomnijmy, że główne krzywizny powierzchni to wartości własne operatora kształtu, główne kierunki krzywizny to jego wektory własne , krzywizna Gaussa jest jej wyznacznikiem , a średnia krzywizna to połowa jej śladu . Odwrotność operatora kształtu zawiera te same wartości dla promieni krzywizny.

Podstawiając do równania różniczkę , otrzymujemy: ${\ displaystyle {\ vec {x}} _ {d}}$

${\ Displaystyle \ częściowe {\ vec {x}} _ {d} = \ częściowe {\ vec {x}} - \ częściowe {\ vec { n}} S_ {n} ^ {-1}, \ quad}$ gdzie ${\ Displaystyle S_ {n}}$ jest operatorem kształtu dla ${\ Displaystyle {\ vec {d }}({\vec {n}}({\vec {u}}))}$ .

Następnie ponownie używamy równań Weingartena , aby zastąpić ${\ Displaystyle \ częściowe {\ vec {n}}}$ :

$quad}$${\ Displaystyle \ częściowe {\ vec {x}} _ {d} = \ częściowe {\ vec {x}} + \ częściowe {\ vec {x}} SS_ {n} ^ {- 1},$${\ Displaystyle {\ vec {x}} ({\ vec { u}})}$ gdzie jest $operatorem$ kształtu dla .

$aby$ rozwiązujemy dla i mnożymy obie strony przez ${\ Displaystyle -S},$ wrócić do równań Weingartena tym razem ${ \ Displaystyle \ częściowe {\ vec {x}} _ {d}}$ :

${\ Displaystyle \ częściowe {\ vec {x}} _ {d} (I + SS_ {n} ^ {- 1}) ^ {-1}=\częściowy {\vec {x}},}$

${\ Displaystyle - \ częściowe {\ vec {x}} _ {d} (I + SS_ {n} ^ {-1}) ^ {- 1} S = - \ częściowe {\ vec {x}} S = \ częściowy {\vec {n}}.}$

Zatem ${\ Displaystyle S_ {d} = (I + SS_ {n} ^ {- 1}) ^ {- 1} S}$ i odwracając obie strony daje nam ${\ Displaystyle S_ {d} ^ {- 1} = S ^ {-1} + S_ {n} ^ {- 1}}$ .

Zobacz też

• Mapowanie wypukłości
• Funkcja odległości i funkcja odległości ze znakiem
• Pole odległości
• Druk offsetowy
• Sąsiedztwo rurowe

• Josef Hoschek: Przesunięcie krzywych w płaszczyźnie. W: CAD. 17 (1985), s. 77–81.
• Takashi Maekawa: Przegląd przesuniętych krzywych i powierzchni. W: CAD. 31 (1999), s. 165–173.

Dalsza lektura

• Farouki, RT; Neff, Kalifornia (1990). „Właściwości analityczne krzywych przesunięcia płaszczyzny”. Projektowanie geometryczne wspomagane komputerowo . 7 (1–4): 83–99. doi : 10.1016/0167-8396(90)90023-K .
•   Piegl, Les A. (1999). „Obliczanie przesunięć krzywych i powierzchni NURBS”. Projektowanie wspomagane komputerowo . 31 (2): 147–156. CiteSeerX 10.1.1.360.2793 . doi : 10.1016/S0010-4485(98)00066-9 .
•   Porteous, Ian R. (2001). Zróżnicowanie geometryczne: dla inteligencji krzywych i powierzchni (wyd. 2). Wydawnictwo Uniwersytetu Cambridge. s. 1–25. ISBN 978-0-521-00264-6 .
•   Patrikalakis, Nicholas M.; Maekawa, Takashi (2010) [2002]. Badanie kształtu na potrzeby komputerowego wspomagania projektowania i produkcji . Springer Science & Business Media. Rozdział 11. Odsuń krzywe i powierzchnie. ISBN 978-3-642-04074-0 . Darmowa wersja internetowa .
• Anton, Franciszek; Emiris, Ioannis Z.; Mourrain, Bernard; Teillaud, Monique (maj 2005). „O ustawiony na krzywą algebraiczną i zastosowanie do stożków”. Międzynarodowa konferencja na temat informatyki i jej zastosowań . Singapur: Springer Verlag. s. 683–696.
•   Farouki, Rida T. (2008). Krzywe pitagorejskie-hodograph: algebra i geometria nierozłączne . Springer Science & Business Media. s. 141–178. ISBN 978-3-540-73397-3 . Wymienione strony to materiał ogólny i wprowadzający.
•   Au, CK; Mam, Y.-S. (2013). „Obliczanie krzywych przesunięcia za pomocą funkcji odległości: rozwiązanie kluczowego wyzwania związanego z generowaniem ścieżki narzędzia skrawającego”. W Ma, Y.-S. (red.). Modelowanie semantyczne i interoperacyjność w inżynierii produktów i procesów: technologia dla informatyki inżynierskiej . Springer Science & Business Media. s. 259–273. ISBN 978-1-4471-5073-2 .

Linki zewnętrzne

• Krzywe równoległe w MathWorld
• Słownik wizualny krzywych płaszczyzny Xah Lee
• http://library.imageworks.com/pdfs/imageworks-library-offset-curve-deformation-from-Skeletal-Anima.pdf aplikacja do animacji; opatentowany jako http://www.google.com/patents/US8400455
• http://www2.uah.es/fsegundo/Otros/Offset/16-SanSegundoSendraSendra-1532.pdf