Pierścień logiczny

W matematyce pierścień logiczny R jest pierścieniem , dla którego x ² = x dla wszystkich x w R , czyli pierścieniem składającym się tylko z elementów idempotentnych . Przykładem jest pierścień liczb całkowitych modulo 2 .

Każdy pierścień Boole'a daje początek algebrze Boole'a , z mnożeniem pierścienia odpowiadającym koniunkcji lub spotkaniu ∧ i dodawaniem pierścienia do wyłącznej alternatywy lub różnicy symetrycznej (nie alternatywy ∨, która stanowiłaby półpierścień ). I odwrotnie, każda algebra Boole'a daje początek pierścieniowi Boole'a. Pierścienie Boole'a zostały nazwane na cześć twórcy algebry Boole'a, George'a Boole'a .

Notacje

Istnieją co najmniej cztery różne i niekompatybilne systemy notacji dla pierścieni i algebr Boole'a:

• W algebrze przemiennej standardową notacją jest użycie x + y = ( x ∧ ¬ y ) ∨ (¬ x ∧ y ) dla sumy pierścieni x i y oraz użycie xy = x ∧ y dla ich iloczynu.
• W logice powszechną notacją jest użycie x ∧ y dla spotkania (tak samo jak iloczyn pierścieniowy) i użycie x ∨ y dla łączenia, podanego w notacji pierścieniowej (podanej tuż powyżej) przez x + y + xy .
• W teorii mnogości i logice powszechne jest również używanie x · y dla spotkania i x + y dla łączenia x ∨ y . To użycie + różni się od użycia w teorii pierścieni.
• Rzadką konwencją jest użycie xy dla iloczynu i x ⊕ y dla sumy pierścieniowej, aby uniknąć niejednoznaczności +.

Historycznie termin „pierścień Boole'a” był używany na oznaczenie „pierścienia Boole'a prawdopodobnie bez tożsamości”, a „algebra Boole'a” była używana na oznaczenie pierścienia Boole'a z tożsamością. Istnienie tożsamości jest konieczne, aby uznać pierścień za algebrę na ciele dwóch elementów : w przeciwnym razie nie może być (jednostkowego) homomorfizmu pierścienia ciała dwóch elementów w pierścieniu boolowskim. (Jest to to samo, co stare użycie terminów „pierścień” i „algebra” w teorii miary ).

Przykłady

Jednym z przykładów pierścienia boolowskiego jest zbiór potęgowy dowolnego zbioru X , gdzie dodanie w pierścieniu jest różnicą symetryczną , a mnożenie jest przecięciem . Jako inny przykład możemy również rozważyć zbiór wszystkich skończonych lub koskończonych podzbiorów X , ponownie z symetryczną różnicą i przecięciem jako operacjami. Mówiąc bardziej ogólnie, przy tych operacjach każde pole zbiorów jest pierścieniem boolowskim. Zgodnie z twierdzeniem Stone'a o reprezentacji każdy pierścień Boole'a jest izomorficzny z ciałem zbiorów (traktowanym jako pierścień z tymi operacjami).

Związek z algebrami Boole'a

Diagramy Venna dla operacji logicznych koniunkcji, alternatywy i dopełnienia

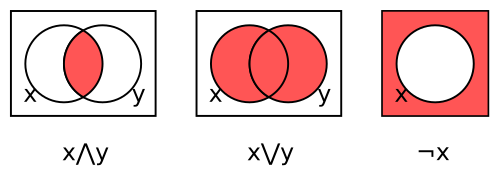
Ponieważ operacja łączenia ∨ w algebrze Boole'a jest często zapisywana addytywnie, w tym kontekście sensowne jest oznaczanie dodawania pierścieni przez ⊕, symbol często używany do oznaczania wyłączności lub .

Biorąc pod uwagę pierścień boolowski R , dla x i y w R możemy zdefiniować

x ∧ y = xy ,

x ∨ y = x ⊕ y ⊕ xy ,

¬ x = 1 ⊕ x .

Te operacje następnie spełniają wszystkie aksjomaty dla spotkań, połączeń i dopełnień w algebrze Boole'a . W ten sposób każdy pierścień Boole'a staje się algebrą Boole'a. Podobnie każda algebra Boole'a staje się pierścieniem Boole'a w następujący sposób:

xy = x ∧ y ,

x ⊕ y = ( x ∨ y ) ∧ ¬( x ∧ y ).

Jeśli pierścień Boole'a jest tłumaczony w ten sposób na algebrę Boole'a, a następnie algebra Boole'a jest tłumaczona na pierścień, wynikiem jest oryginalny pierścień. Analogiczny wynik zaczyna się od algebry Boole'a.

Odwzorowanie między dwoma pierścieniami Boole'a jest homomorfizmem pierścieni wtedy i tylko wtedy, gdy jest homomorfizmem odpowiednich algebr Boole'a. Ponadto podzbiór pierścienia Boole'a jest ideałem pierścienia (ideał pierścienia pierwszego, ideał pierścienia maksymalnego) wtedy i tylko wtedy, gdy jest ideałem rzędu (ideał pierwszego rzędu, ideał maksymalnego rzędu) algebry Boole'a. Pierścień ilorazowy pierścienia Boole'a modulo a ideał pierścienia odpowiada algebrze czynnikowej odpowiedniej algebry Boole'a modulo odpowiedniego ideału rzędu.

Własności pierścieni boolowskich

Każdy pierścień logiczny R spełnia x ⊕ x = 0 dla wszystkich x w R , ponieważ wiemy

x ⊕ x = ( x ⊕ x ) ² = x ² ⊕ x ² ⊕ x ² ⊕ x ² = x ⊕ x ⊕ x ⊕ x

a ponieważ ( R ,⊕) jest grupą abelową, możemy odjąć x ⊕ x od obu stron tego równania, co daje x ⊕ x = 0. Podobny dowód pokazuje, że każdy pierścień logiczny jest przemienny :

x ⊕ y = ( x ⊕ y ) ² = x ² ⊕ xy ⊕ yx ⊕ y ² = x ⊕ xy ⊕ yx ⊕ y

a to daje xy ⊕ yx = 0, co oznacza xy = yx (używając pierwszej właściwości powyżej).

Własność x ⊕ x = 0 pokazuje, że dowolny pierścień Boole'a jest algebrą asocjacyjną na ciele F ₂ z dwoma elementami, dokładnie w jeden sposób. W szczególności każdy skończony pierścień logiczny ma jako liczność potęgę dwójki . Nie każda algebra asocjacyjna jednostek jednostkowych na F ₂ jest pierścieniem boolowskim: rozważmy na przykład pierścień wielomianowy F ₂ [ X ].

Pierścień ilorazowy R / I dowolnego pierścienia boolowskiego R modulo dowolnego ideału I jest znowu pierścieniem boolowskim. Podobnie każdy podpierścień pierścienia boolowskiego jest pierścieniem boolowskim.

Każda lokalizacja $pierścienia$ logicznego $jest$ zbiór pierścieniem boolowskim, ponieważ każdy lokalizacji

Maksymalny pierścień ilorazów $)$ w sensie Utumi i Lambeka pierścienia logicznego R pierścieniem boolowskim, ponieważ każdy częściowy endomorfizm jest

Każdy ideał pierwszy P w pierścieniu boolowskim R jest maksymalny : pierścień ilorazowy R / P jest dziedziną całkową , a także pierścieniem boolowskim, więc jest izomorficzny z ciałem F ₂ , które pokazuje maksymalność P . Ponieważ ideały maksymalne są zawsze pierwszymi, ideały pierwsze i ideały maksymalne pokrywają się w pierścieniach boolowskich.

Każdy skończenie wygenerowany ideał pierścienia Boole'a jest główny (w rzeczywistości ( x , y ) = ( x + y + xy )). Ponadto, ponieważ wszystkie elementy są idempotentami, pierścienie boolowskie są przemiennymi regularnymi pierścieniami von Neumanna , a zatem są absolutnie płaskie, co oznacza, że ​​każdy moduł nad nimi jest płaski .

Zjednoczenie

Ujednolicenie w pierścieniach boolowskich jest rozstrzygalne , to znaczy istnieją algorytmy do rozwiązywania dowolnych równań na pierścieniach boolowskich. Zarówno unifikacja, jak i dopasowywanie w skończenie generowanych swobodnych pierścieniach boolowskich są NP-zupełne i oba są NP-trudne w skończenie przedstawionych pierścieniach boolowskich. (W rzeczywistości, ponieważ każdy problem unifikacji f ( X ) = g ( X ) w pierścieniu boolowskim można zapisać jako problem dopasowania f ( X ) + g ( X ) = 0, problemy są równoważne.)

Ujednolicenie w pierścieniach boolowskich jest jednolite, jeśli wszystkie niezinterpretowane symbole funkcji są zerowe i finitarne w przeciwnym razie (tj. jeśli symbole funkcyjne niewystępujące w sygnaturze pierścieni boolowskich są wszystkie stałymi, to istnieje najbardziej ogólny unifikator , a poza tym minimalny kompletny zbiór unifikatorów jest skończony).

Zobacz też

• Postać normalna sumy pierścieniowej

Dalsza lektura

•   Atiyah, Michael Francis ; Macdonald, IG (1969), Wprowadzenie do algebry przemiennej , Westview Press, ISBN 978-0-201-40751-8
•   Fraleigh, John B. (1976), pierwszy kurs algebry abstrakcyjnej (wyd. 2), Addison-Wesley , ISBN 978-0-201-01984-1
• Herstein, IN (1975), Topics In Algebra (wyd. 2), John Wiley & Sons
•   McCoy, Neal H. (1968), Wprowadzenie do algebry współczesnej (red. Poprawiona), Allyn and Bacon , LCCN 68015225
• Riabuchin, Yu. M. (2001) [1994], „Pierścień boolowski” , Encyklopedia matematyki , EMS Press

Linki zewnętrzne

• John Armstrong, Pierścienie Boole'a